基于扩展多项式集的一种串行乘法器设计*

苏丹丹

(罗定职业技术学院教育系，广东 罗定 527200)

基于扩展多项式集的一种串行乘法器设计*

苏丹丹

(罗定职业技术学院教育系，广东 罗定 527200)

基于多项式基定义了扩展多项式集，利用其形式表示有限域F2n中的元素.通过分析多项式集下的乘法运算公式，设计出一种有效的串行乘法器，仅需n个异或门和n+1个门数.

有限域；多项式集；乘法器；复杂性

有限域在编码理论、计算机通信和密码学中有广泛的应用,特别是基于有限域F2n上的椭圆曲线密码体制以其短密钥、高强度等优点引起人们的高度重视.在椭圆曲线密码体制中,如AES标准椭圆曲线加密算法、RSA算法等，有限域上的乘法运算极大地影响各种密码算法的速度.因此,设计复杂性低的有限域的算法和乘法器已成为研究热点[1].

关于有限域F2n上的乘法器的研究,按照参加运算的元素的形式来分有3种[2]:正规基、多项式基(或标准基)和对偶基.根据具体的实现方式，分为并行乘法器和串行乘法器.目前,各种形式的乘法器都在不断被研究和比较.文献[3]提出一种II型最优正规基并行乘法器设计方案.文献[4] 基于II型最优正规基设计了一个串行乘法器，但利用最优正规基在计算过程中都需要先将域元素的正规基表示转换为多项式基表示,在多项式基下做乘法运算,再将结果转换为正规基表示.文献[5]中提出基于弱对偶基下的比特并行乘法器,这个过程涉及到最优弱对偶基的选择和多项式基与弱对偶基之间的变换.由于对偶基乘法和正规基乘法中都存在基底转换问题,因此当有限域的维数变大时,乘法器的电路规模将会急剧增大,对椭圆曲线密码系统设计不宜.选择利用多项式基设计乘法器,避免了基与基之间的转换.另一方面,在并行乘法器中，随着并行的增多，乘法运算和加法运算会增加，往往导致运行速度的下降，而串行乘法器以牺牲运行速度为代价来获得更好的性能.因此，如何选择串行或并行乘法器取决于它的应用性质.

笔者在多项式基的基础上定义了扩展多项式集，利用扩展多项式集形式表示有限域F2n中的元素，打破了传统的利用移位多项式基底表示元素的方法，避免了多项式基和移位多项式基底的转换，同时使得任意两元素相乘得到的结果既简单又规则.

1 相关概念和定义

定义1[6]设N={α0,α1,…,αn-1}是F2n在F2上的一组基，若存在β∈F2n，使得αi=βi(0≤i≤n-1),则称N为一组多项式基，即N形如{1,α,…,αn-1}.

定义2 当N={1,α,…,αn-1}是F2n在F2上的多项式基时，称N′={1,α,…,αn-1,αn}为扩展多项式集.

定义3[7]系数全部为1的多项式称为全一多项式(All￣One￣Polynomial,AOP).次数为n的AOP多项式为AOP(x)=xn+xn-1+…+x2+x+1，有如下基本性质:(ⅰ)(x-1)AOP(x)=xn+1-1；(ⅱ)AOP多项式是不可约多项式当且仅当n+1是素数,且2是模n+1的本原根.

2 算法原理

域F2n由F2上的n次不可约多项式产生,不可约多项式的选择在有限域乘法器的执行中也扮演着重要角色,为计算简便，选取AOP多项式.

设f(x)=xn+xn-1+…+x2+x+1 是F2上的一个不可约AOP多项式且α是f(x)的根,F2n=F2/(f(x))，是F2的n次扩域.由代数知识可知,f(x)是α的极小多项式,且αn+αn-1+…+α=1,αn+1=1.

对∀a∈F2n，其多项式基表示为

a=an-1αn-1+an-2αn-2+…+a1α+a0ai∈F2,0≤i≤n-1.

∀A∈F2n，用扩展多项式集表示为

A=Anαn+An-1αn-1+…+A1α+A0An=0，Ai∈F2,0≤i≤n-1.

由αn+1=1可知：

又i,j∈[0,n]，于是0≤i+j≤2n，若i+j≡n(modn+1)，则必有i+j=n，即

(1)

记AB=D=D0+D1α+…+Dn-1αn-1+Dnαn.其中：

D0=A1Bn+A2Bn-1+…+An-1B2+AnB1+A0B0,

D1=A2Bn+A3Bn-1+…+AnB2+A0B1+A1B0,

…

Dn=A0Bn+A1Bn-1+…+An-2B2+An-1B1+AnB0.

将(1)式用矩阵表示为

因为矩阵方程中含n+1个向量，所以包含n+1个输入门和n个异或门.

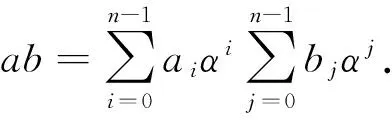
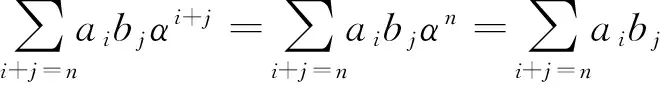
从而

(2)

记ab=d0+d1α+…+dn-1αn-1.由(1)，(2)式知,(1)式易于用矩阵表示，(2)式如用矩阵表示，方阵中元素是和的形式，较复杂；乘积结果表达式中，(1)式中αi(0≤i≤n)的系数更简洁,规律更明显,这就决定了采用算法1在实际操作和乘法器设计中呈现较大的优势，用C语言实现的算法如下:

main()

{int A[N]={A0,A1,A2,…,An},

B[N]={B0,B1,B2,…,Bn};

int i,j,k,N=n+1;

int D[N];

for(k=0;k<=N-1;k++)

for(i=0;i<=N-1;i++)

for(j=0;j<=N-1;j++)

{if((i+j)%N=k)

{D[k]=D[k]+A[i]*B[j];}

}

for(k=0;k<=N-1;k++)

{printf(″%d″,D[k]);}

}

3 乘法器设计

根据上述算法,设计的乘法器结构如图1所示.

图1 基于扩展多项式集上的乘法运算实现过程

利用扩展多项式集表示元素，使得乘积运算简便快捷，在乘法器的设计中减少了硬件的消耗，仅需异或门数为n,与门数为n+1.

[1] MASOLEH A R.Efficient Algorithms and Architcctures for Field Multiplication Using Gaussian Normal Bases[J].IEEE Transactions on Computers,2006,55(1):34-47.

[2] KOC C K,SUNAR B.Low￣Complexity Bit￣Parallel Canonical Normal Basis Multipliers for a Class of Finite Fields[J].IEEE Transactions on Computers,1998,47(3):353-356.

[3] SUNAR B,KOC C K.An Efficient Optimal Normal Basis Type Ⅱ Multiplier[J].IEEE Transactions on Computers,2001,50(5):83-87.

[4] 王庆先，孙世新,方 冰.基于Ⅱ型最优正规基的串行乘法器[J].系统工程与电子技术,2005,27(8)：65-69.

[5] 曾晓洋，魏仲慧，郝志航.弱对偶基下比特并行RS编码器的设计[J].光电工程，2001,28(3)：1 494-1 496.

[6] QUTTINEH N H.Computational Complexity of Finite Field Multiplication[M].Examensarbete Utforti Datatransmission vid Linkopings Tekniska Hogskola,Linkoping,2003.

[7] RUDIN W.数学分析原理[M].英文版.北京：机械工业出版社，2004.

(责任编辑 向阳洁)

SerialMultiplierBasedonExtendedPolynomialSet

SU Dandan

(Deptartment of Education,Luoding Vocational Polytechnic,Luoding 527200,Guandong China)

The extended polynomial set is defined based on the polynomial basis,which represents the element of the finite fieldF2n.The multiplying formula is analyzed carefully.An efficient serial multiplier is proposed,which needs onlynXOR gates andn+1 AND gates.

finite field;polynomial set;multiplier;complexity

1007-2985(2014)03-0028-03

2013-12-26

国家自然科学基金资助项目(10990011);四川省杰出青年学术带头人培育计划项目(2011JQ0037)

苏丹丹(1980-)，女，湖北随州人，罗定职业技术学院教育系讲师，硕士，主要从事应用数论研究.

TP301.1

A

10.3969/j.issn.1007-2985.2014.03.007