紊流滑动轴承油膜承载力的近似解

张永芳, 刘 成, 王 东, 武 澎

(1. 西安理工大学 印刷包装工程学院,西安 710048；2. 重庆大学 机械传动国家重点实验室,重庆 400030；3. 中国煤炭科工集团西安研究院,西安 710077；4. 西安机电信息技术研究所,西安 710065)

由于滑动轴承具有工作平稳、承载力大、噪声小等优点，被广泛应用于高速、重载和高精度旋转机械当中。滑动轴承作为轴承转子系统的重要支承部件，其本质是非线性的，目前已有许多对其非线性特性进行研究的报道。吕延军[1-3]对滑动轴承支承的转子系统的非线性动力学行为进行了研究。通过运用变分约束原理求解了固定瓦-可倾瓦滑动轴承的非线性油膜力及其动力学特性系数[1]；运用Castelli方法，基于数据库原理，快速求解了固定瓦-可倾瓦滑动轴承润滑的Reynolds方程[2]；运用微分变换法并结合非线性理论，分析了固定瓦-可倾瓦气体润滑径向轴承-刚性转子系统的不平衡响应及轴承参数对系统非线性行为的影响规律[3]。目前，许多学者在研究滑动轴承的非线性动力学特性时，润滑油膜大多采用层流假设，但是随着轴承-转子系统运行工况要求的不断提高，使得转子运行的线速度增大，目前许多实际工作中的轴承已在紊流工况下运转。王小静等[4-6]对复合型紊流润滑理论模式及其应用进行了深入研究。采用该复合型紊流润滑理论研究高速重载滑动轴承问题时，尤其能够适用其强轴向流的特点，能较准确地分析滑动轴承的紊流润滑性能。虽然该理论很先进，但求解十分复杂、费时，如果采用数据库的方法，虽然能使该理论的计算量大大缩减，但仍然无法得到近似解析解。Chang-Jian等[7]对紊流滑动轴承支承的转子系统的分岔和混沌等非线性行为进行了研究。通过采用长轴承假设模型(即忽略了沿轴向变化的压力流)，得到了紊流长轴承假设下的解析表达式。Lo[8]分析了具有耦合应力影响的紊流径向轴承支承的柔性转子系统的非线性动力学行为，采用了短轴承的假设(即忽略了沿周向变化的压力流)。无论是“无限短轴承模型”[8-9]或“无限长轴承模型”[7,10]，它们均是被广泛使用的假设，并且都是在Reynolds方程的基础上做了相应的简化后得到的。由于实际应用的轴承宽径比通常在0.8～1之间，无论是采用无限长或无限短轴承模型计算得到的结果均与其相差甚远。因此我们需要寻求对有限长轴承能够进行快速求解的方法。采用渐进法[11-13]求解流体润滑的Reynolds方程，可以近似分析流体膜的润滑问题，但通常在较小的偏心率和载荷范围内用来近似分析。Buckholz等[14]运用渐进法并结合Ocvirk的短轴承近似解，提出了一种提高无限短轴承假设解精度的方法。Hirani等[15]和Bastani等[16]分别将短轴承和长轴承解的不同组合用于有限长轴承的计算分析。这些研究都给寻求紊流有限长滑动轴承油膜承载力的近似解析方法提供了参考。

本文利用多参数摄动原理，采用零方程模式的Constantinescu理论即Prandtl混合长度润滑理论模式，对有限长紊流滑动轴承的Reynolds方程进行了求解，得到了紊流有限长轴承承载力的近似解析表达式，同时分析了偏心率、宽径比等参数对承载力及压力分布的影响。

1 紊流状态下的Reynolds方程

图1给出了紊流径向滑动轴承示意图及其计算坐标；图2为紊流动压轴承的剖面图。图1中，Ob为轴承中心，Oj为轴颈中心，φ是从y轴负方向顺时针转至油膜位置的角度，θ为偏位角，φ是从OjOb延长线顺时针方向转至油膜位置的角度，fr和ft分别为作用在轴颈上的非线性油膜力径向和切向分量，fx和fy分别为作用在轴颈上的非线性油膜力在x和y轴负方向的分量。h为油膜厚度，ω为转子角速度，R为轴承半径，r为轴颈半径，mg为轴承载荷。图2中，B为轴承宽度。

紊流滑动轴承有量纲Reynolds方程为：

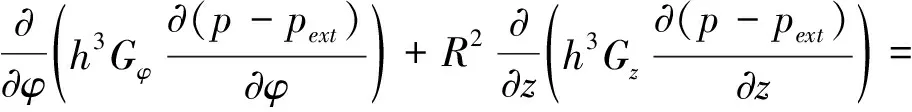
(1)

式中，Gφ和Gz为紊流因子[17]，

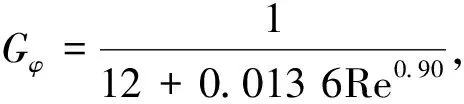
对式(1)进行无量纲化，为此引入以下无量纲变量：

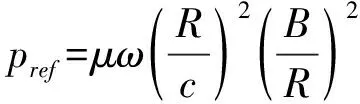
将上式代入式(1)可得无量纲Reynolds方程：

(2)

令：

(3)

式中，pp为平均压力。

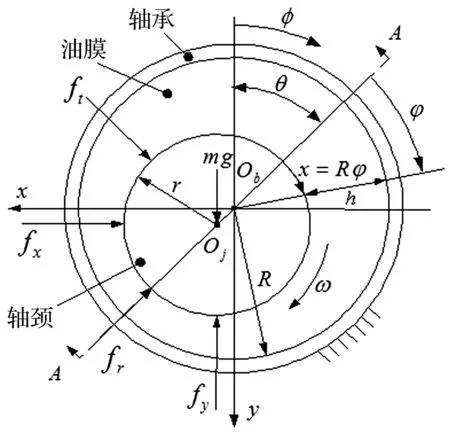
图1 紊流滑动轴承示意图及其计算坐标

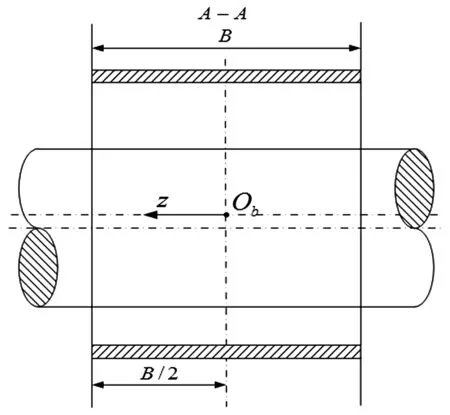
图2 紊流滑动轴承剖面图

引入Sommerfeld 和Ocvirk数：

(4)

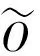
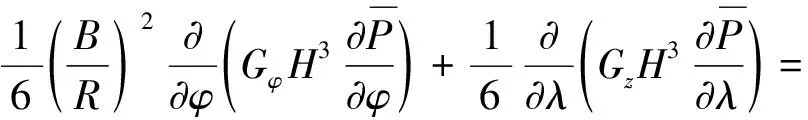
(5)

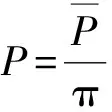
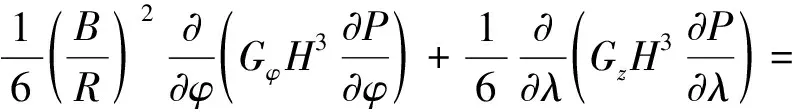
(6)

2 非线性油膜承载力的近似解

由于Reynolds方程求解出的油膜压力是一些独立变量(φ,λ, …)以及一些参变量 (ζ,B/d,… )的函数。为方便计算起见，令：

(7)

将P展开成ζ的幂级数：

P=P0+ζP1+ζ2P2+ζ3P3+…

(8)

因为Ocvirk数O是ζ的函数，所以也将O展开成ζ的幂级数：

O=O0+ζO1+ζ2O2+ζ3O3+…

(9)

由于所取项数的增加，使求解趋于繁琐，加大了计算的困难，所以这里取：

(10)

将式(10)代入式(6)可得：

(11)

对于上式，令ζ=0可得：

(12)

由边界条件：当λ=±1/2时，P0=0得到：

(13)

对P0求一次导数可得：

(14)

对式(14)两端同乘以H3得：

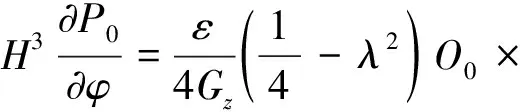
(15)

对式(15)求一次导数可得：

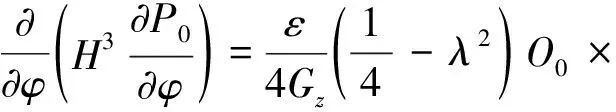
(16)

为计算方便起见令：

将上式代入式(16)可得：

(17)

所以有：

(18)

对式(13)求两次导数且两端同乘以H3/6可得：

(19)

将式(18)和式(19)代入式(11)可得：

对上式积分两次并代入边界条件可得：

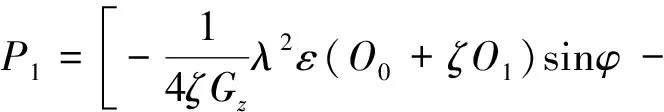
(21)

由于P0和P1中有未知量O0和O1，所以需要求解O0和O1。因为有：

(22)

式中，F=2ppπRB为承载力，有量纲Fx和Fy分别为承载力在x和y方向上的分量，且有：

(23)

将式(23)代入式(22)可得：

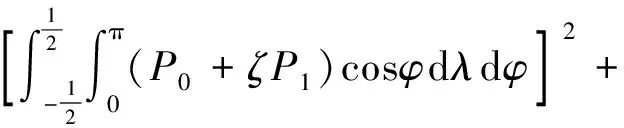
(24)

将式(13)代入式(24)并令ζ=0可得：

(25)

由上式计算可得：

(26)

将式(13)和式(21)代入式(24)，略去ζ的二阶小量可得：

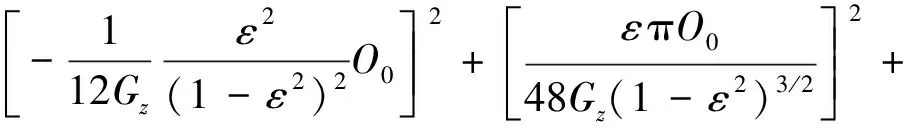
(27)

将式(13)代入式(27)可得：

(28)

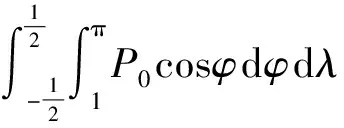
(29)

式中，

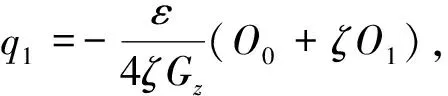
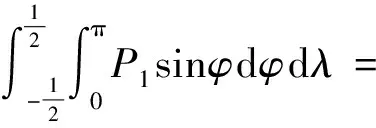
(30)

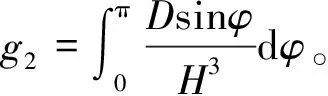
令：

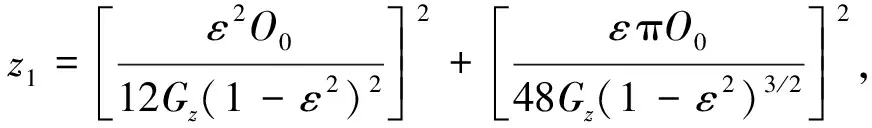
将上式及式(29)和式(30)代入式(28)可得：

(31)

将式(26)和式(31)代入式(10b)可得O，将式(13)和式(21)代入式(10a)可得油膜压力P。

3 计算结果分析

运用以上方法求得了Ocvirk数和油膜压力，从而求得了油膜承载力。当偏心率ε=0.5时，绘出了分别运用本文方法和有限元法[18]求得的油膜承载力随宽径比B/d变化的曲线对比图，如图3所示。从图3可以看出，当偏心率ε=0.5时，运用本文方法和有限元法解出的油膜承载力F随宽径比B/d变化的曲线比较接近，从而验证了本文方法求解的正确性。图中油膜承载力的差别主要源于两种求解方法所采用的边界条件的不同。有限元法采用的是下游Reynolds边界条件(即工程实际中油膜存在的破裂边界条件)，而本文提出的方法采用的是半Sommerfeld边界条件。如果有限元法采用半Sommerfeld边界条件，则本文方法得到的近似解将和有限元法的结果吻合得更好。图4为宽径比B/d=0.25时，0阶Ocvirk数O0随偏心率ε的变化曲线图。从图4可以看出，在宽径比B/d=0.25时，随着偏心率ε的增大，0阶Ocvirk数O0的值不断减小且接近于0，图中表明Ocvirk数的主要部分O0即0阶Ocvirk数O0在偏心率ε大于0.2时的变化比较缓慢。图5为宽径比B/d=0.5时，Ocvirk数O随偏心率ε的变化曲线图。图5示出当B/d=0.5时，Ocvirk数O随着偏心率ε的增大而逐渐减小。对比图4可知：Ocvirk数与0阶Ocvirk数O0相比受偏心率影响较明显。图6是在轴向位置λ=0处，宽径比B/d=0.5，ε=0.1和ε=0.8时，无量纲油膜压力P的主要部分P0即0阶无量纲油膜压力随轴承周向坐标φ的变化曲线图(图中示出了不同偏心率下的P0随φ的变化曲线图)。图6表明，偏心率较大时，压力P的主要部分P0即0阶无量纲油膜压力P0(当B/d→0时的无量纲油膜压力)随φ的增大呈现出剧烈变化，由图6中可以看出，在周向位置角较小时，随着周向位置角φ的增加0阶无量纲油膜压力P0增加；当周向位置角较大时，随着周向位置角φ的增加，P0减小。图7是在轴向位置λ=0处，当宽径比B/d=0.5和偏心率ε=0.8时，无量纲油膜压力P随周向坐标φ的变化曲线图。与图6类似，0阶无量纲油膜压力P0和无量纲油膜压力P随着周向坐标的变化先增大后减小；对比图6，无量纲油膜压力P的变化趋势与0阶无量纲油膜压力P0的变化趋势一致。

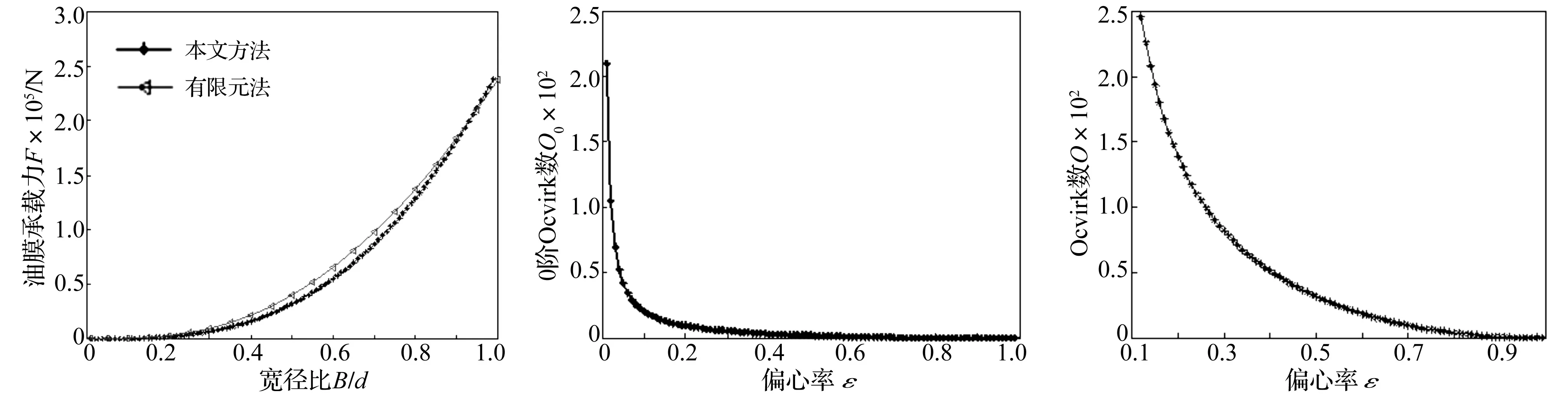
图3 偏心率ε=0.5时，油膜承载力F随宽径比B/d变化的曲线图

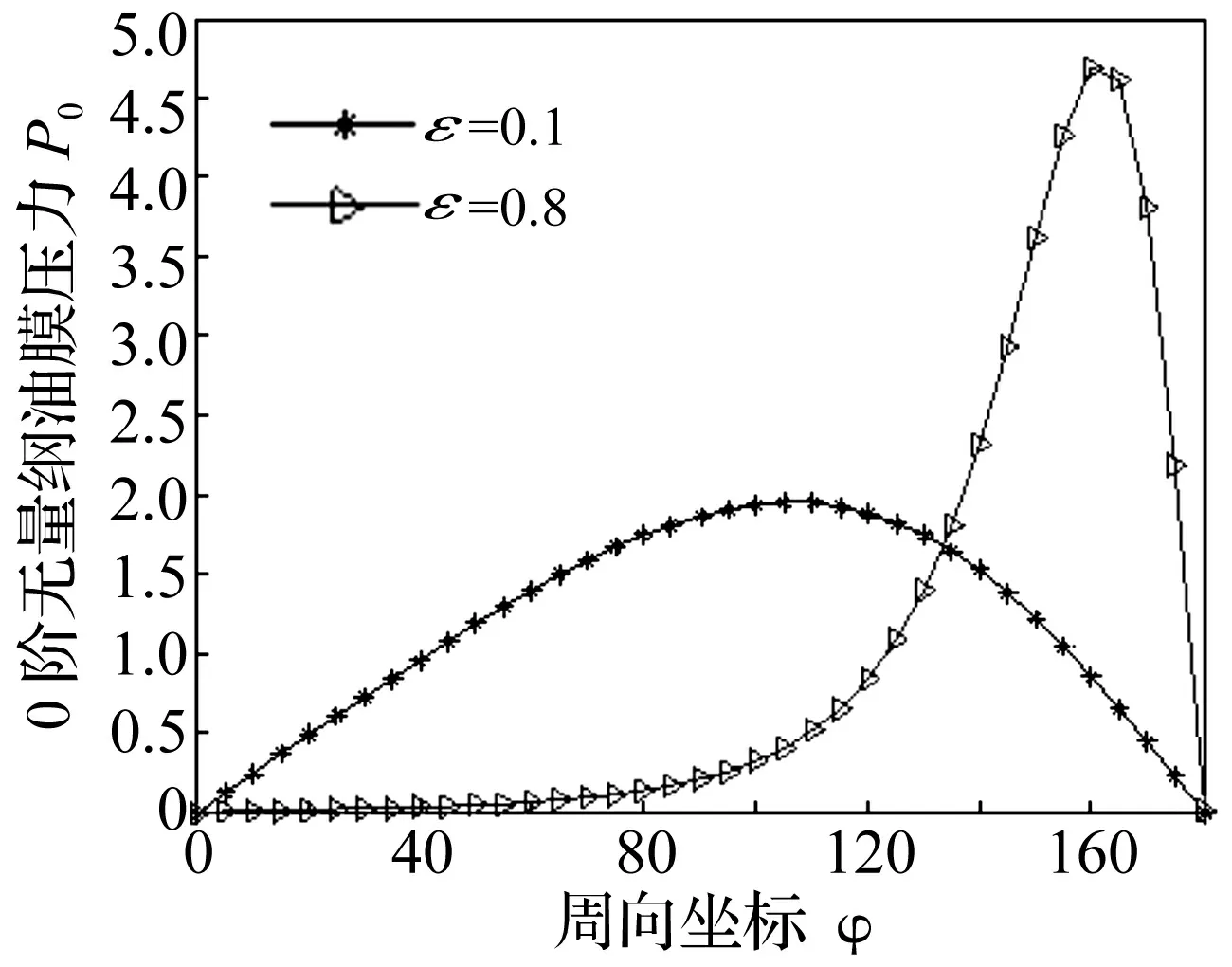
图6 宽径比B/d=0.5，λ=0处，偏心率ε=0.1和ε=0.8时0阶无量纲油膜压力P0随周向坐标φ的变化曲线图

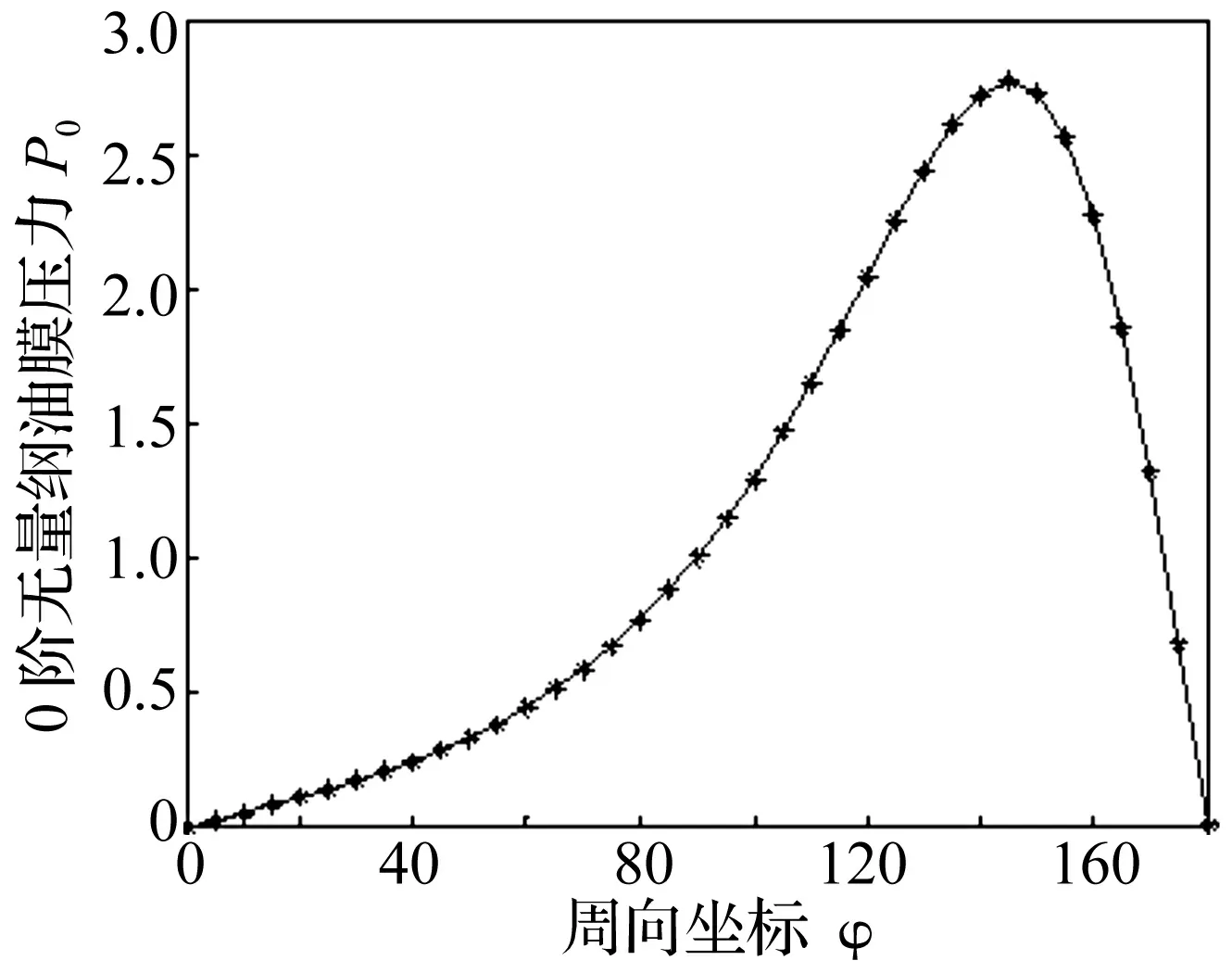
图7 宽径比B/d=0.5时，λ=0处，无量纲油膜压力P随周向坐标φ的变化曲线图

4 结 论

运用多参数原理，结合Sommerfeld和Ocvirk数，求解得到了有限长紊流滑动轴承非线性油膜承载力的近似解析解，在此基础上分析了油膜压力随偏心率、宽径比等参数的变化规律。本文的方法在较大的偏心率和载荷范围内适用，可为紊流滑动轴承支承转子系统的设计提供理论参考。

参 考 文 献

[1]Lu Y J, Ji L F, Zhang Y F, et al. Dynamic behaviours of the rotor non-linear system with fixed-tilting-pad journal bearings support[J]. Journal of Engineering Tribology, 2010, 224(10): 1037-1047.

[2]吕延军，张永芳，于扬冰，等.固定瓦-可倾瓦组合径向轴承-柔性转子系统非线性运动分析[J].振动与冲击，2011,30(5):257-262.

LÜ Yan-jun, ZHANG Yong-fang, YU Yang-bing, et al. Nonlinear dynamicanalysis of a flexible rotor system with combinedfixed-tilting pad journal bearing[J]. Journal of Vibration and Shock, 2011, 18(3): 257-262.

[3]Lu Y J, Zhang Y F, Shi X L, et al. Nonlinear dynamic analysis of a rotor system with fixed-tilting-pad self-acting gas-lubricated bearings support[J]. Nonlinear Dynamics, 2012, 69(3): 877-890.

[4]王小静, 张直明, 孙美丽. 复合型紊流润滑理论模式的研究[J]. 摩擦学学报, 2000, 20(2): 127-130.

WANG Xiao-jing, ZHANG Zhi-ming, SUN Mei-li. A combined theory for turbulence in lubricating films[J]. Tribology, 2000, 20(2): 127-130.

[5]王小静, 苏荭, 张直明, 基于复合型紊流润滑理论的径向滑动轴承紊流润滑性能的研究[J]. 机械工程学报, 2003, 39(3): 85-89.

WANG Xiao-jing, SU Hong, ZHANG Zhi-ming. Study on the performance of journal bearing in turbulent regime with the combined Reynolds stress model[J]. Chinese Journal of Mechanical Engineering, 2003, 39(3): 85-89.

[6]王小静, 张直明, 孙美丽. 复合型紊流润滑理论在周隙密封紊流润滑研究中的应用[J]. 摩擦学学报, 2002, 22(4s): 359-362.

WANG Xiao-jing, ZHANG Zhi-ming, SUN Mei-li. Application of combined Reynolds stress turbulent model to the study of plain seal[J]. Tribology, 2002, 22(4s): 359-362.

[7]Chang-Jian C W, Chen C K. Bifurcation and chaos analysis of a flexible rotor supported by turbulent long journal bearings[J]. Chaos, Solitons and Fractals, 2007, 34(4): 1160-1179.

[8]Lo C Y, Chang-Jian C W. Nonlinear dynamics of a flexible rotor supported by turbulent journal bearings with couple stress fluid[J]. Chaos, Solitons and Fractals, 2008, 37(4): 1002-1024.

[9]Sommerfeld A. Zur hydrodynamic theorie der Schmiermittelreibung[J]. Zeitschrift für Mathematik und Physik, 1904, 50(1-2): 97-155.

[10]DuBois G B, Ocvirk F W. Analytical derivation and experimental evaluation of short-bearing approximation for full journal bearings[J]. NACA Report, 1953, 1157:1199-1230.

[11]Nayfeh A H. Perturbation methods[M]. New York: John Wiley & Sons, 1973, 1-25.

[12]Ling F F. Asymptotic analyses in isothermal fluid film lubrication theories[J]. SIAM (Society for Industrial and Mathematics) Review, 1986, 28(3): 343-366.

[13]Capriz G, Cimatti G. On some singular perturbation problems in the theory of lubrication[J]. Applied Mathematics and Optimization, 1977, 4(1): 285-297.

[14]Buckholz R H, Hwang B. The accuracy of short bearing theory for Newtonian lubricants[J]. Journal of Tribology, 1986, 108(1): 73-79.

[15]Hirani H, Athre K, Biswas S. Dynamically loaded finite length journal bearings: analytical method of solution[J]. Journal of Tribology, 1999, 121(4): 844-852.

[16]Bastani Y, Queiroz M D. A new analytic approximation for the hydrodynamic forces in finite-length journal bearings[J]. Journal of Tribology, 2010, 132(1): 014502-1-9.

[17]张直明,张言羊, 谢友柏, 等.滑动轴承的流体动力润滑理论[M]. 北京: 高等教育出版社, 1986, 120-143.

[18]吕延军, 张永芳, 季丽芳, 等. 固定瓦-可倾瓦滑动(轴承转子非线性系统的动力特性分析[J]. 中国电机工程学报, 2010, 30(20): 79-87.

LÜ Yan-jun, ZHANG Yong-fang, JI Li-fang, et al. Analysis of dynamic characteristics of rotor nonlinear system supported by fixed-tilting pad journal bearings[J]. Proceedings of the CSEE, 2010, 30(20): 79-87.