串列布置受扰超高层建筑脉动风压谱特性研究

韩 宁， 顾 明

(同济大学 土木工程防灾国家重点实验室，上海 200092)

建筑结构上的脉动风压谱代表了来流湍流以及流体结构交互作用产生的湍流脉动对建筑表面风压脉动能量的贡献。已有针对高层建筑脉动风压谱的研究主要集中在单体建筑。文献[1-4]研究的是低矮和大跨屋盖表面脉动风压谱和特征湍流间的关系，并试图给出屋面典型区域的脉动风压谱模型。文献[5-7]则针对单体高层建筑典型测点的脉动风压谱进行了研究，指出迎风面脉动风压谱能量主要反映了来流湍流脉动特性，而侧风面脉动风压谱在由前缘过渡到后缘过程中，由于流体再附作用会导致其高频段能量显著增加。叶丰等[8]系统研究了超高层建筑风压的频域特性，通过对水平向和垂直向典型测点脉动风压谱的分析指出侧风面脉动风压能量要大于其他立面且主要集中在漩涡脱落处。然而针对高层建筑风压谱干扰特性的研究较少，kim等[9]研究了受扰建筑典型测点脉动风压功率谱特性，其主要研究的是中轴线处竖向3个典型测点在不同高度比和风向角下的风压谱特性，发现当施扰建筑高度较高时中轴线处的功率谱均向高频区域移动。

本文基于大规模刚性模型测压风洞试验数据，对串列布置受扰超高层建筑沿水平向典型测点风压谱进行了细致的研究，首先给出了单体方形超高层建筑风压谱的特征，然后研究了干扰状态下风压谱特性，主要分析了施扰位置和高度比的影响。

1 风洞试验介绍

试验在同济大学土木工程防灾国家重点实验室TJ-2风洞进行。TJ-2风洞为闭口回流式矩形接口风洞，试验段宽3 m、高2.5 m、长15 m。采用被动模拟方法在TJ-2风洞模拟了我国建筑结构荷载规范(GB50009-2001)[10]中的C类风场(风速剖面指数α=0.22)，几何缩尺比为1∶400。试验采用日本建筑荷载规范(AIJ2004)[11]建议的紊流度公式。详细的平均风速剖面和紊流度剖面的模拟结果与理论值的比较见文献[12]。

图1 串列布置模型示意图

图2 施扰建筑模型示意图

试验模型尺寸为900 mm×150 mm×150 mm的方柱，几何缩尺比为1∶400。在模型上共计布置496个测点，每个立面上均有124个测点，4个面测点布局相同，均在模型的最上部和棱边处布置较密的测点,具体的测点布置图见文献[12]。考虑施扰模型位置变化的影响时，串列布置选取6个典型位置，并列布置选取4个典型位置，斜列布置选取6个典型位置。详细的施扰位置见文献[13]。本文仅分析串列布置时受扰建筑风压谱特性，如图1所示。考虑施扰模型高度变化的影响时，施扰模型横截面均为150 mm×150 mm，高度分别为测试模型高度的0.7，1.0和1.3倍(即高度比ηh取0.7，1.0和1.3)。

2 单体典型测点脉动风压系数自功率谱特性

通过已有研究[14]发现，当两建筑串列布置时，受扰建筑迎风和侧风面测点的干扰效应显著，所以在对功率谱分析时，本文仅选取迎风面和侧风面上的典型测点进行研究。图3是单体建筑风压谱特性分析时选取的典型测点示意图。图中符号含义定义如下，以“N11-3”为例，其中N代表立面名称，11代表测点所在的层序号，3代表该层测点编号。这里测点11层对应于接近(2/3) H高度。

图3 单体分析时选用的典型测点示意图

测点风压系数由下式给出：

Cpi(t)=(Pi(t)-P∞)/(P0-P∞)

(1)

式中，Pi(t)为模型上第i测点处的表面风压值，P0和P∞则分别为参考点处的平均总压和平均静压。参考点高度取为屋顶高度。图4给出的是根据式(1)计算得到的单体建筑立面上的典型测点风压系数时程。

图4 典型测点风压系数时程曲线

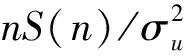
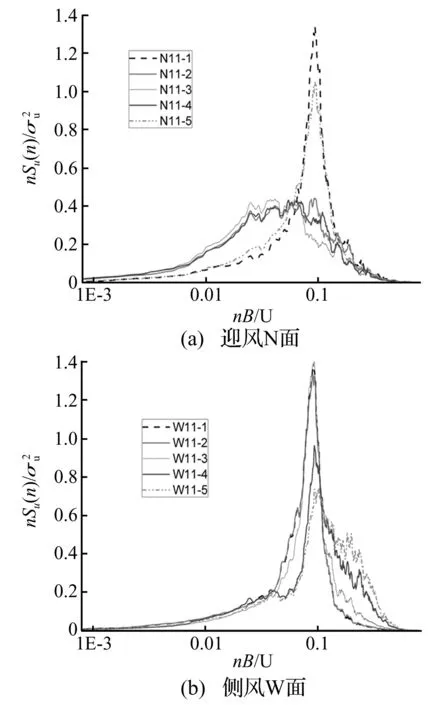
图5 单体建筑典型测点风压谱曲线

图5中给出了0°风向角下单体方形建筑同一高度处迎风N面和侧风W面10个典型测点的风压谱曲线。由图5(a)可见迎风N面测点风压谱形状随位置发生变化且主要分为两类：第一是靠近棱边处测点的谱曲线在折算频率0.09～0.1附近出现尖锐谱峰，这表明棱边处流体发生分离并且产生漩涡脱落。第二是中部测点的谱曲线均为宽频分布，没有尖锐谱峰出现，但低频段能量要远大于棱边附近测点风压谱在低频段的能量，说明迎风N面中间区域主要受来流湍流控制。在高频段迎风N面中轴线测点的谱值略小于棱边附近测点谱值，这或许是由于棱边区域受流体分离影响相比中轴线处要大的原因[2]。在图5(b)中，沿水平方向侧风W面由于受到来流分离、漩涡脱落和瞬态再附的影响，测点风压谱曲线均在折算频率为0.09～0.1附近出现尖锐谱峰，但中轴线前缘谱峰幅值显著大于后缘且谱峰对应的折算频率略有增加。侧风W面谱曲线的另一个显著特征是：在由前缘向后缘移动中，谱曲线高频段衰减斜率增大且高频段能量显著增大，这可能是前缘分离流在后缘发生瞬态再附所致[5-7]。

3 受扰建筑典型测点脉动风压系数自功率谱特性

根据前文中对单体建筑迎风面和侧风面上测点风压谱曲线特征的分析，这里选取更为典型的测点来分析干扰状态下的谱曲线特征。详细的测点选择如图6所示。

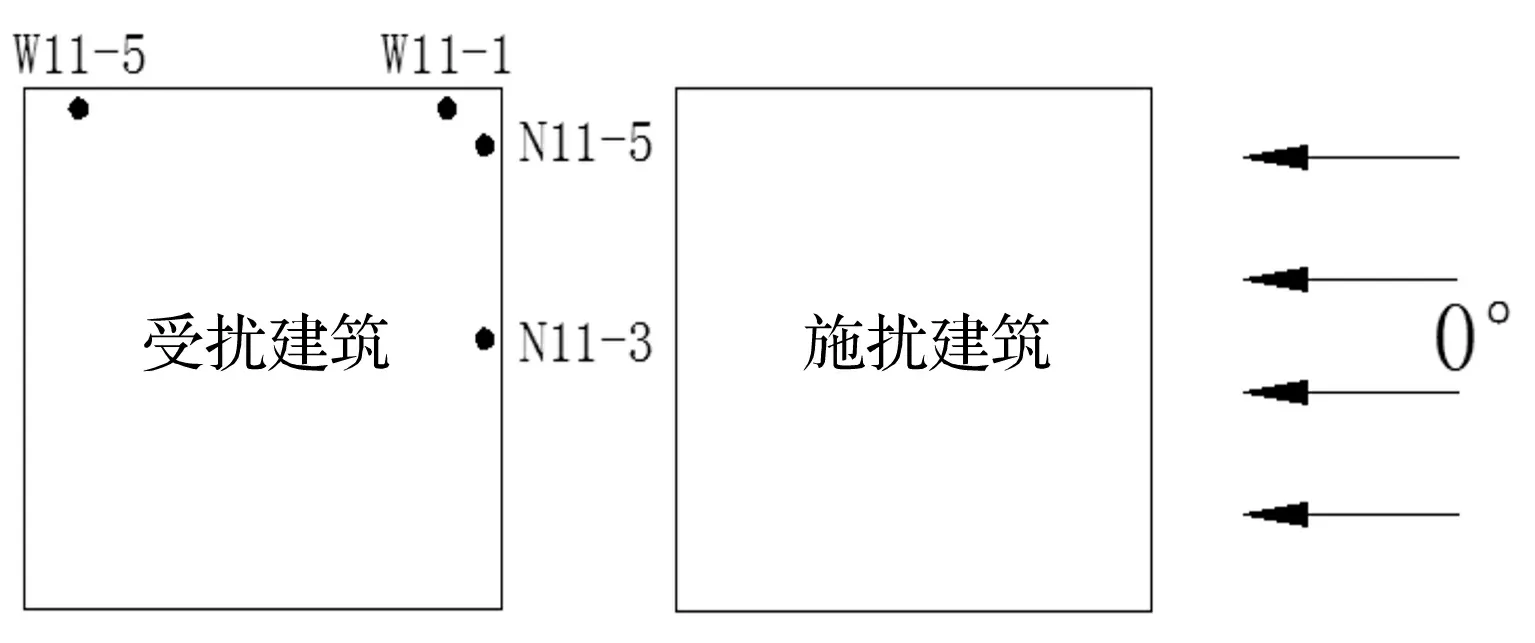
图6 受扰分析时选用的典型测点示意图

3.1 串列布置条件下间距比的影响

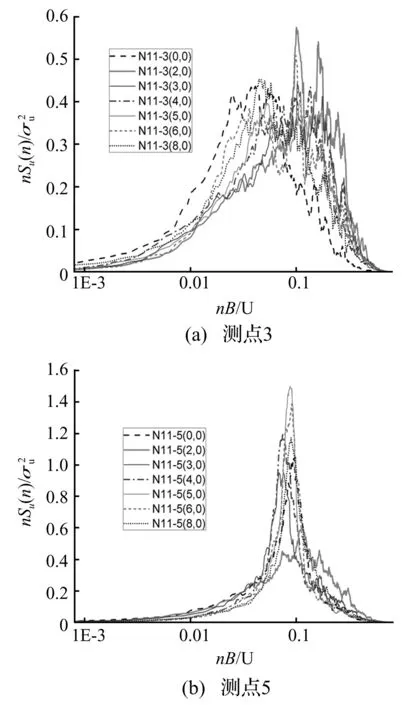
图7 串列布置迎风N面典型测点风压谱曲线

图7是0°风向角下串列布置时受扰建筑迎风N面上典型测点脉动风压谱曲线。图中括号内数字代表串列布置时的相对位置，为了分析方便用符号Sx代表[13]。由图可以看出，除Sx=2.0外，棱边处测点的谱值均大于中轴线处测点谱值。在图7(a)中，任意间距比Sx下中轴线测点3的谱曲线和单体建筑相比均显著向高频区域移动，高频段能量显著增加而低频段能量显著减小，这表明串列布置下干扰效应在迎风N面中轴线处产生的小尺度漩涡增多，减小了来流湍流脉动产生的大尺度漩涡。随间距比Sx增大，干扰效应减弱，谱曲线逐渐向单体状态时靠近。特殊的是，在Sx≤3.0时，测点3的谱曲线出现驼峰现象，但谱值要小于侧风面漩涡脱落引起的谱值，间接说明间距比较小时，两建筑间形成了回旋涡。在图7(b)中，迎风N面近棱边测点5的谱曲线形状相比单体建筑变化不大，任意间距比Sx下谱曲线均在折算频率0.07～0.1出现尖锐谱峰，但当Sx=2.0时，谱曲线仅出现弱谱峰，谱峰幅值相比单体显著减小且峰值频率由0.1右移到折算频率0.12附近，频率变得更丰富。和中轴线测点3相比，棱边测点5的高频段能量相比单体建筑增加程度较小，但Sx=2.0处却显著增大；其低频段能量相比单体均有减小，但Sx=2.0处减小程度最小。这说明，当间距比较小时，受扰建筑迎风面会处于上游施扰建筑后形成的分离剪切层当中，此时受扰建筑迎风面棱边附近的流体分离减弱，高频段能量增大。

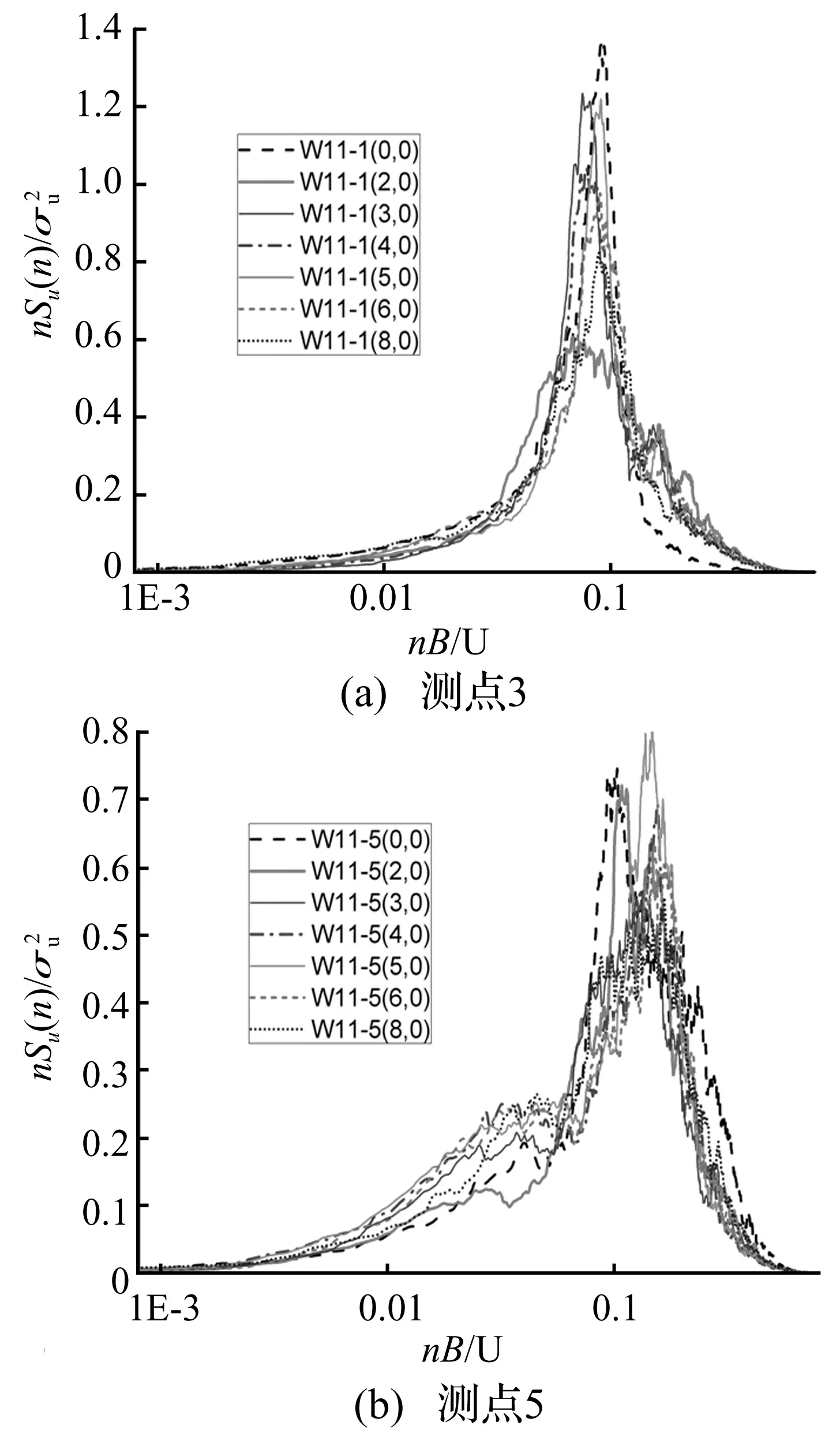
图8 串列布置侧风W面典型测点风压谱曲线

图8是0°风向角下串列布置时受扰建筑侧风W面上典型测点脉动风压谱曲线。由图可以看出，除Sx=2.0外，前缘棱边测点能量均大于后缘棱边测点。在图8(a)中，和单体建筑相比，谱曲线形状变化不大，任意间距比Sx下前缘棱边测点1的谱曲线均出现尖锐谱峰，但谱峰值相比单体建筑减小，说明施扰建筑存在时，该处漩涡脱落强度减弱，尤其是在Sx=2.0处，谱曲线的谱峰宽而平坦，峰值频率无法确定，说明间距比较小时，上游施扰建筑分离流产生的剪切层抑制了该点的漩涡脱落，导致谱峰消失而高频段能量显著增大。施扰建筑存在时，测点高频段能量均显著大于单体建筑且间距比Sx的影响不大；而低频段能量均略小于单体建筑且(3,0)处减小程度最大。据此可以推断，上游施扰建筑会在受扰建筑侧风面前缘区域发生再附，所以其小尺度漩涡数量相比单体建筑显著增加。由图8(b)可以看出，W立面后缘棱边测点5的谱曲线形状相对单体没有显著变化，仅在中频段存在弱谱峰，但峰值频率向高频区域移动，由单体建筑的0.1右移到0.12～0.2之间，也即施扰建筑存在时后缘处主导漩涡的尺度减小。但和单体建筑相比，高频段能量均略有减小且间距比Sx的影响不大；低频段能量除Sx=2.0外均大于单体建筑，说明施扰建筑存在时，再附区域向侧风面的前缘移动，而漩涡逐渐形成也即后缘区域小尺度漩涡相比单体减少，大尺度漩涡相比单体略有增多。

3.2 串列布置条件下高度比的影响

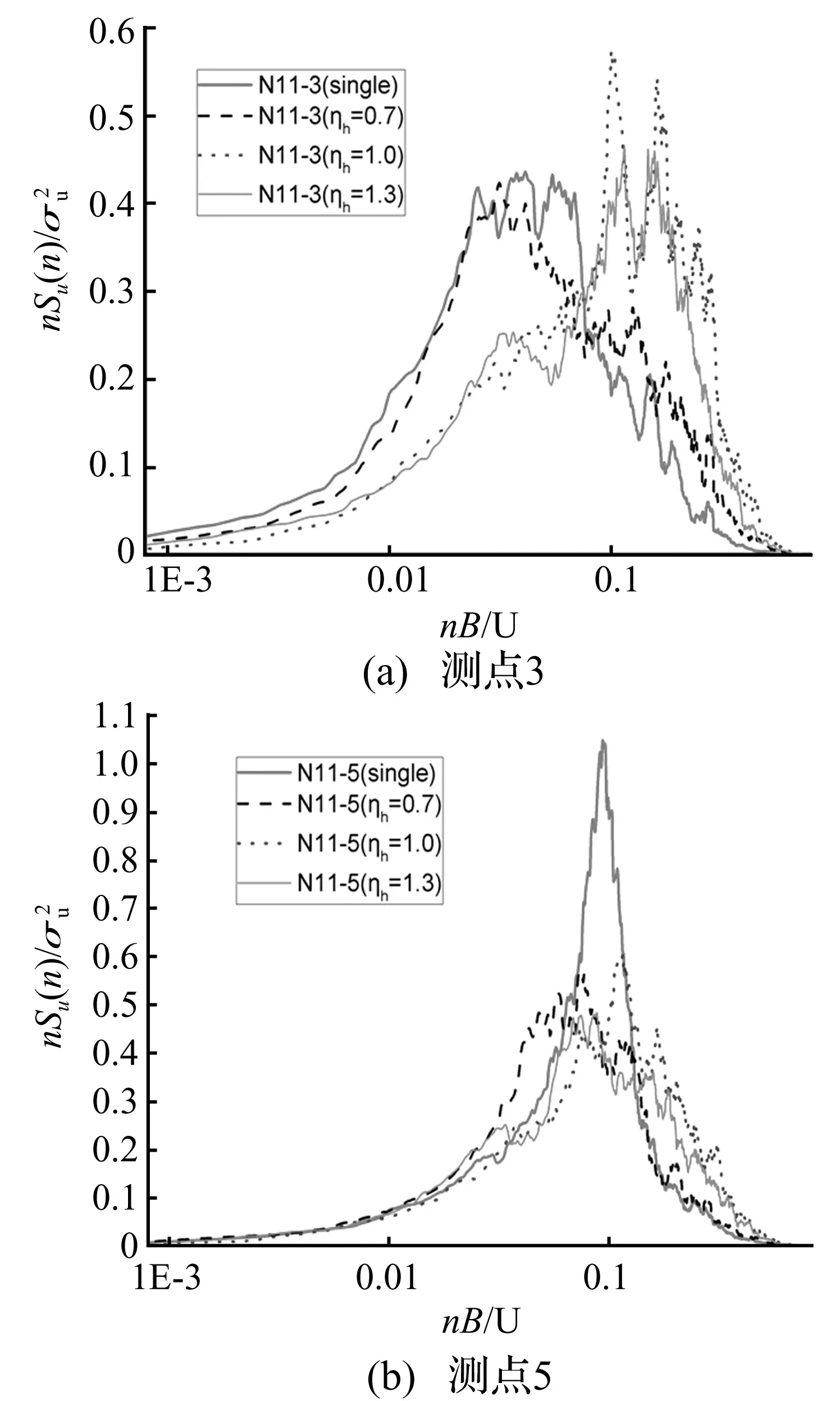
图9 典型串列位置处不同高度比迎风N面典型测点风压谱曲线

图9是0°风向角下典型串列位置(2,0)处受扰建筑迎风N面典型测点风压谱曲线随高度比变化的示意图。由图9(a)可以看出，中轴线测点3的谱曲线在ηh≥1.0时的功率谱曲线形状类似，和单体建筑相比，其整体向高频区域显著移动[9]；但ηh=0.7时该高度处测点3的功率谱曲线和单体建筑接近，仅在高频段谱值增大且没有出现驼峰现象，说明该串列布置间距比下回旋流对高度处的测点影响较小。两建筑高度越接近时，引起的特征湍流越大，而来流湍流影响越小，所以高频段能量在ηh=1.0取得最大值。在图9(b)中，和ηh=0.7时N立面近棱边测点5的谱曲线形状相比ηh≥1.0时的谱曲线整体向高频区域移动且ηh=1.0时的谱值略大，也即两建筑等高时对迎风2/3高度处棱边测点的流场影响显著。

图10 典型串列位置处不同高度比侧风W面典型测点风压谱曲线

图10是0°风向角下典型串列位置(2,0)处受扰建筑侧风W面典型测点风压谱曲线随高度比变化的示意图。由图10(a)可以看出，前缘棱边测点1的谱曲线在任意高度比ηh下均出现谱峰，但谱峰幅值相比单体建筑减小且ηh=1.0时的谱峰幅值最小。当间距比Sx较小时，两建筑等高会导致侧风W面2/3高度处漩涡脱落程度减弱最多。但此时高频段能量在ηh=1.0时最大，或许是由于上游施扰建筑分离剪切层中夹带的小尺度漩涡较多。在图10(b)中，W立面后缘测点5的谱曲线形状在ηh≥1.0时接近且谱峰值随高度比增大而增大；但ηh=0.7时的谱曲线谱峰消失，能量分布在较宽的频带上且频率丰富，低频段能量显著大于ηh≥1.0时的对应低频段能量。由此说明该高度处的再附区域在高度比ηh=0.7时受到的影响最显著。

4 结 论

基于刚性模型风洞测压试验，对0°风向角下方形受扰高层建筑迎风面和侧风面上典型测点的脉动风压谱特性进行了分析，得出如下结论：

(1) 单体方形高层建筑在迎风面中轴线区域的风压谱曲线均为宽频分布而在棱边区域则出现尖锐谱峰，说明迎风面中间区域主要受来流湍流控制而棱边处则受流动分离影响显著。侧风面的谱曲线均出现尖锐谱峰且自前缘向后缘过渡时，由于流体再附，高频段能量显著增大。

(2) 受扰建筑和施扰建筑串列布置时，任意间距比Sx下，靠近前缘棱边测点的风压谱曲线形状和单体建筑类似，谱曲线依然存在尖锐谱峰。Sx<3.0时受扰建筑处于上游施扰建筑形成的剪切层包围中，谱峰幅值相比单体建筑显著减小。但在迎风面中轴线处，功率谱曲线均向高频区域移动，值得注意的是Sx<3.0时，由于回旋流产生会出现驼峰现象，而在侧风面后缘测点，施扰建筑存在导致再附区域发生变化，所以低频段能量要大于单体建筑而高频段则相对减小。

(3) 串列布置间距比较小时，和ηh=0.7时相比，迎风面测点在2/3高度处的功率谱曲线在ηh≥1.0时均向高频区域移动且ηh=1.0的谱值最大，而ηh=1.3时在侧风面上的谱值最大。

(4) 通过对测点风压功率谱的分析，从频域角度更清晰得看出围护结构表面风压在不同干扰因素下的变化规律，最后得出了有意义的结论，从而对幕墙结构设计给出定性参考。

参 考 文 献

[1]Kumar K S, Stathopoulos T. Power spectra of wind pressures on low building roofs[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1998, (74-76):665-674.

[2]Kumar K S, Stathopoulos T. Wind loads on low building roofs: a stochastic perspective[J]. Journal of Structural Engineering, ASCE, 2000, 126(8):944-956.

[3]孙瑛,许楠,武岳.考虑特征湍流影响的体育场悬挑屋盖脉动风压谱模型[J].建筑结构学报,2010, 31(10):24-33.

SUN Ying, XU Nan, WU Yue. Spectral model of fluctuating wind pressure on grandstand roofs with consideration of signature turbulence[J]. Journal of Building Structures, 2010, 31(10):24-33.

[4]樊友川,黄鹏,顾明,等.工业厂房屋面脉动风荷载及干扰效应试验研究[J].土木工程学报,2010, 43:297-306.

FAN You-chuan, HUANG Peng, GU Ming et al. Experimental study on fluctuating wind loadings and the interference effects on industrial building roof[J]. China Civil Engineering Journal,2010, 43:297-306.

[5]Kareem A, Cermak J E. Pressure fluctuations on a square building model in boundary layer flows[J]. J. Wind Eng. Ind. Aerodyn., 1984, 16 (1): 17-24.

[6]Surry D, Djakovich D. Fluctuating pressures on tall buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1995, 58(1-2): 81-112.

[7]Kim Y M. Pressure fluctuations on a tall building with square cross section[J]. Proceedings of International Symposium on Wind and Structures (Cheju, Korea, 2000), Techno-Press, 2000:393-405.

[8]叶丰,顾明.超高层建筑风压的频域特性[J].同济大学学报(自然科学版) ,2006,3(34):285-292.

YE Feng, GU Ming. Frequency characteristics of wind pressure on super-tall buildings[J]. Journal of Tongji University(Natural Science) ,2006,3(34):285-292.

[9]Kim W, Tamura Y, Yoshida A. Interference effects of local peak pressures acting on walls of tall buildings[J]. Proceedings of 11th Americas Conference on Wind Engineering, San Juan, Puerto Rico, 2009.

[10]建筑结构荷载规范(GB 50009-2001)(2006版)[S]. 中国建筑工业出版社,2006.

[11]Architectural Institute of Japan, AIJ 2004. Recommendations for loads on buildings[S]. Tokyo: Architectural Institute of Japan, 2004.

[12]韩宁,顾明.两串列方柱局部脉动风压干扰研究: 第1部分 迎风面效应[J].振动与冲击,2009,28(12):188-192.

HAN Ning, GU Ming. Interference effects on local fluctuating pressure of two square tall buildings in tandem arrangement: Part 1 windward side effects[J]. Journal of Vibration and Shock,2009, 28(12):188-192.

[13]韩宁,顾明.两并列方形高层建筑局部风压干扰特性研究[J]. 同济大学学报(自然科学版),2011,10(39): 1441-1446.

HAN Ning, GU Ming. Interference effects on wind pressure of two square tall buildings in side-by-side arrangement [J]. Journal of Tongji University(Natural Science) , 2011,10(39): 1441-1446.

[14]韩宁,顾明.两串列方形高层建筑局部风压干扰特性分析[J].土木建筑与环境工程,2011,5(33):13-22.

HAN Ning, GU Ming. Characteristics of interference effects on local pressure of two square tall buildings in tandem arrangement [J]. Journal of Civil, Architectural & Environmental Engineering, 2011, 5 (33):13-22.