筒承式钢筋混凝土立筒群仓的自由振动分析
2014-09-05龚耀清李烨君王录民许启铿
龚耀清, 李烨君, 王录民, 许启铿, 揣 君
(1.河南理工大学 土木工程学院,河南 焦作 454000;2.河南工业大学 土木建筑学院,郑州 450007)
随着工农业生产的不断发展,钢筋混凝土立筒仓的应用日趋增多,其结构体系的力学特性与动力性能受到了诸多学者和工程技术人员的关注,有关规范[1-2]也有相应的计算方法和规定。
然而,现有的分析与研究成果基本上都是针对单个立筒仓[3-9],实际工程中的钢筋混凝土立筒仓大多数是以立筒群仓的形式出现[10-12]。钢筋混凝土立筒群仓是由单仓通过仓体连接,整体浇注而形成的一个整体,其结构性能完全不同于单仓。因此,对钢筋混凝土立筒群仓的动力特性进行研究有着十分重要的理论与实际意义。
钢筋混凝土立筒群仓按群仓仓下支承结构可分为筒承式、柱承式及筒柱承式三种,本文研究筒承式钢筋混凝土立筒群仓的自由振动问题。全文共分以下几个部分,首先讨论筒承式钢筋混凝土立筒群仓自由振动的分析模型,在建立计算模型时,将其简化为由n段竖向广义Timoshenko梁构成的组合体;然后利用能量原理,推导筒承式钢筋混凝土立筒群仓自由振动时的运动方程以及相应的边界条件;再利用高质高效的常微分方程求解器[13-14]求算例运动方程的数值解,得到其自振频率和振型,并将数值解与相应的试验数据[15]进行对比,以验证数值方法的有效性和精确性;最后根据数值计算结果、模型试验结果、实际工程背景推出结论。
1 分析模型
图1为文献[15]中筒承式钢筋混凝土立筒群仓结构的抗震试验模型。考虑到群仓是由单仓通过仓体连接,整体浇注在刚度比较大的一个基础之上的对称结构体系,且体系的高度与横向跨度几乎相等。因此,可以断定:在这种结构体系的位移(或运动)中,其水平方向的剪切变形和弯曲变形一样,都是主要的变形形式,必须同时考虑。

图1 试验模型
为此,通过权衡整个结构体系在其轴线x方向的刚度和质量变化规律,将其简化为由四段不同尺寸、不同刚度和不同质量的竖向广义Timoshenko梁(同时考虑弯曲和剪切变形)构成的组合体,如图2所示。
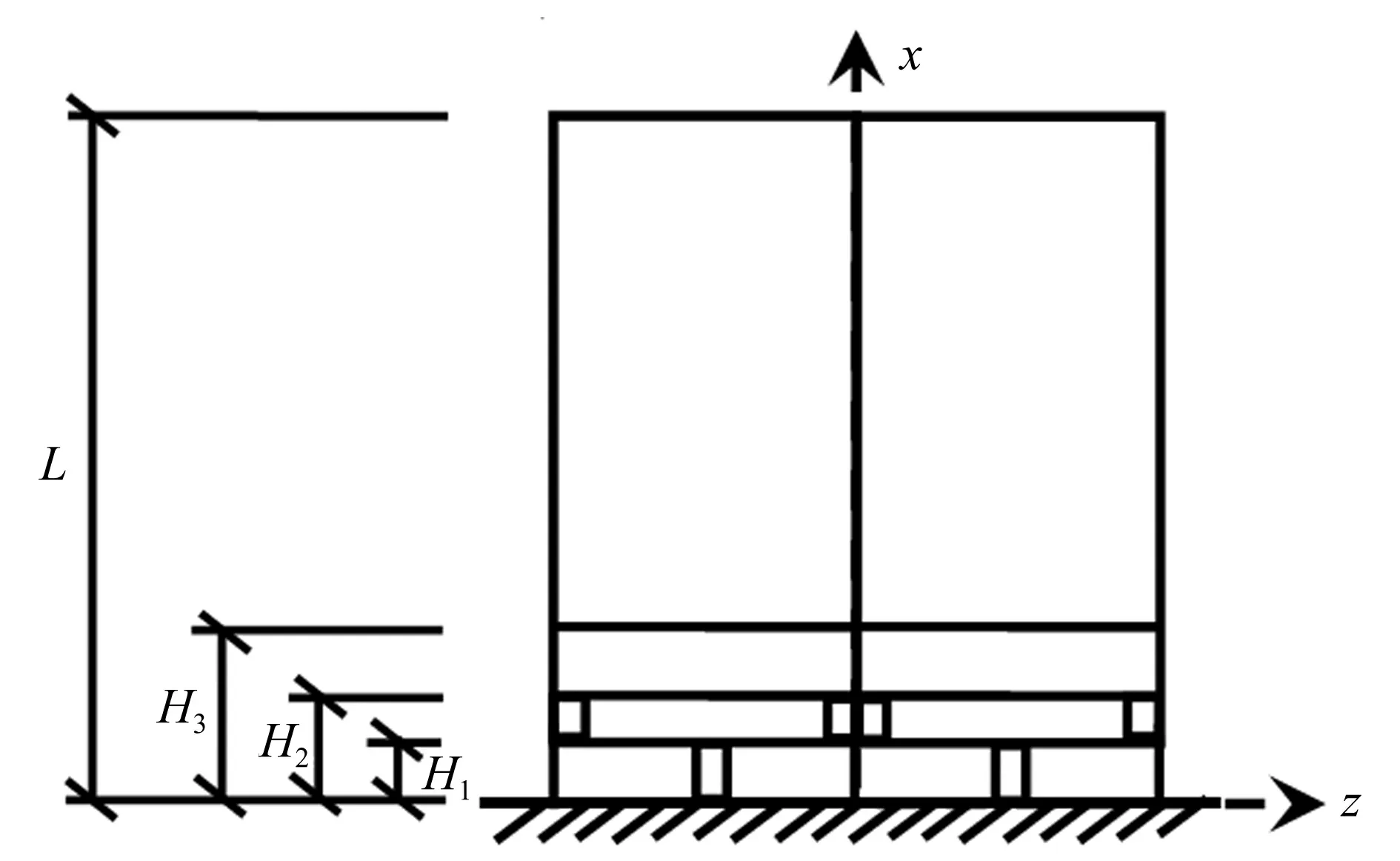
图2 群仓计算模型示意图

图3 群仓计算模型各段横截面示意图
组合体的最底端(第一段)是立筒群仓底部开门的部位,第二段是立筒群仓开窗部位与其对应的部分漏斗的组合,第三段是另一部分漏斗和与其对应的立筒群仓组合,最顶端(第四段)是立筒群仓主体部位,各段横截面如图3所示。
其中:x轴为竖向广义Timoshenko梁组合体的中性面与纵向对称面的交线,y轴为中性面与横截面(由多个单仓横截面组成)的交线,z轴为横截面与纵向对称面的交线。
2 运动方程
选取竖向广义Timoshenko梁组合体各段中性面的挠度Wj(x)和横截面绕中性轴的转角θj(x)为基本未知函数。
其中,j=1,2,…,n表示为群仓在x轴方向的分段数。
对于自由振动,中性面的水平运动W(x,t)和横截面绕中性轴的转动θ(x,t)可表示为:
(1)
其横截面的轴向位移可表示为:
u(z,x,t)=-zθ(x,t)
(2)
于是,结构系统的总势能∏、总动能T分别为:
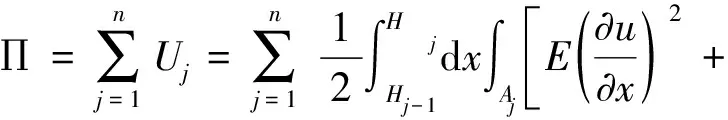
(3)

(4)
式中:ρ为质量密度,A为横截面面积,E为弹性模量,G为剪切模量。
利用哈密顿原理:

(5)
可推导出筒承式钢筋混凝土立筒群仓自由振动时的运动方程以及相应的边界条件如下:
运动方程:
(6)
群仓底部的边界条件(x=0):
(7)
群仓各段连接处(x=Hj,j=1,2,…,n-1)的连接条件:
(8)
群仓顶部的边界条件(x=L):
(9)
上述方程组构成了常微分方程组的特征值问题,其数值解可用常微分方程求解器(ODE solver—COLSYS)[13,14]进行求解。
3 算例与计算结果分析
文献[15]给出了筒承式钢筋混凝土立筒群仓的试验模型,其平面组合为2×3的群仓,几何尺寸和材料特性如下:群仓的总高度L为2.19 m,每个单仓的外直径为0.778 m,仓壁厚度均为0.014 m,弹性模量7.5 GPa,剪切模量为3.0 GPa,密度2 400 kg/m3,群空仓结构自重G1是贮料的三分之一,贮料分布在群仓的上部分(模型中第四段)。第一段的高度(H1)为0.169 m,第二段的高度(H2-H1)为0.094 m,第三段的高度(H3-H2)为0.237 m,第四段的高度(L-H3)为1.69 m。
按前述方法建模并导出运动方程后,可得到与式(6)~(9)相同的运动方程与相应的边界与连接条件(本例j取1~ 4),并考虑到工程实际中的贮料在振动时有减震作用,取贮料的自重G2=3kG1,k是反映谷物减震效果的系数,本文取K=0.85。
利用ODE求解器编程求解方程(6)后,可得出该立筒群仓的自振频率和振型如下:

表1 群空仓前五阶的自振频率(Hz)

图4 群空仓前三阶振型

图5 群满仓前三阶振型

表2 群满仓前五阶的自振频率(Hz)
4 结 论
(1) 如表1、表2所示,在空仓情况下,本文的数值解与试验结果吻合较好,但在满仓情况下,本文的数值解与试验结果相比,频率明显减小,其原因是谷物种类之间的差别、谷物的减震作用等实际因素很难定量确定,从而导致数值计算结果与试验结果有偏差。
(2) 从表1、2及图4、图5可以看出:本文所建模型可以真实地反映该结构体系的动力特性,由于结构体系纵向与横向的尺寸属于同一量级,所以其剪切振动与弯曲振动一样,都起主导作用,各阶振动均为弯、剪耦合振动,各阶振型均为弯曲和剪切的耦合振型。
参 考 文 献
[1]构筑物抗震设计规范 GB 50191-2012 [S]. 北京:中国计划出版社,2012.
[2]钢筋混凝土筒仓设计规范 GB 50077-2003[S]. 北京:中国计划出版社,2003.
[3]Dooms D, Degrande G, De Roeck G, et al. Finite element modelling of a silo based on experimental modal analysis [J]. Engineering Structures, 2006, 28(4): 532-542.
[4]Leszczynski J S, Blaszczyk T. Modeling the transition between stable and unstable operation while emptying a silo [J]. Granular Matter, 2011, 13(4): 429-438.
[5]赵衍刚,江近仁. 筒仓结构的自振特性与地震反应分析[J]. 地震工程与工程振动,1989,9(3):55-64.
ZHAO Yan-gang, JIANG Jin-ren. Vibration properties and earthquake responses of silo structures [J]. Journal of Earthquake Engineering and Engineering Vibration, 1989, 9(3): 55-64.
[6]刘增荣,黄义,邵江. 贮仓结构参数的频域识别[J]. 振动与冲击,2001,20(1):79-81.
LIU Zeng-rong, HUANG Yi, SHAO Jiang. Frequency domain identification of storehouse structure parameters [J]. Journal of Vibration and Shock, 2001, 20(1): 79-81.
[7]孙芳,王命平,耿树江,等. 柱承式筒仓的地震反应分析[J]. 特种结构,2005,22(4):4-9.
SUN Fang, WANG Ming-ping, GENG Shu-jiang, et al. The seismic response analysis of column-supported silos [J]. Special Structure, 2005, 22(4): 4-9.
[8]王命平,孙芳,刘伟,等. 筒仓与地基相互作用对支承柱端弯矩的影响[J]. 世界地震工程,2008,24(2):127-130.
WANG Ming-ping, SUN Fang, LIU Wei, et al. The effect of the silo-foundation interaction on the moment of supporting columns [J]. World Earthquake Engineering, 2008, 24(2): 127-130.
[9]蒋华,谢海舰,张薇. 某筒-柱支承式钢筋混凝土圆形筒仓结构动力特性研究[J]. 西华大学学报(自然科学版),2012,31(1):102-105.
JIANG Hua, Xie Hai-jian, ZHANG Wei, Analysis of dynamic characteristics for cylinder reinforced concrete silo supported by columns-cylinder [J]. Journal of Xihua University (Natural Science), 2012,31(1):102-105.
[10]Lapko A, Prusiel J A. Structural analysis of RC circular grouped silos under patch actions [J]. Granular Matter, 2004, 6(2-3): 185-190.
[11]王命平,孙芳,高立堂,等. 筒承式群仓的地震作用分析及试验研究[J]. 工业建筑,2005,35(10):29-32.
WANG Ming-ping, Sun Fang, Gao Li-tang, et al. Study of earthquake action and tests of multi-silo supported by cylinder [J]. Industrial Construction, 2005, 35(10): 29-32.
[12]王录民,张华,卢文胜,等. 柱承式群仓结构模型模拟地震振动台试验研究[J]. 建筑结构,2010,40(10):41-43.
WANG Lu-min, ZHANG Hua, LU Wen-sheng, et al. Study of shaking table tests on the model of group silos structures [J]. Building Structure, 2010, 40(10): 41-43.
[13]YUAN Si. ODE conversion techniques and their applications in computational mechanics[J]. Acta Mechanica Sinica, 1991, 7(3):283-288.
[14]叶康生,袁驷. 常微分方程特征值问题求解器解法的改进[J]. 工程力学,2004,21(3):33-35.
YE Kang-sheng, YUAN Si. The improvement of ODE solver method in the analysis of ODE eigenvalue problem[J]. Engineering Mechanics, 2004, 21(3):33-35.
[15]张逯见. 筒承式立筒群仓结构模型模拟地震振动台试验研究[D]. 郑州:河南工业大学,2010.
