嵌岩特性对嵌岩桩桩顶纵向振动阻抗的影响研究

吴文兵， 蒋国盛， 窦 斌， 王奎华， 黄生根

(1.中国地质大学 工程学院，武汉 430074；2.浙江大学 滨海和城市岩土工程研究中心，杭州 310058)

近年来，随着嵌岩桩在大型桥梁基础、港口工程、海洋石油钻采平台等工程中被广泛应用，众多国内外学者对嵌岩桩的承载和沉降特性进行了广泛研究[1-14]。黄求顺[2]在山区嵌岩桩试验的基础上，提出了最大嵌岩深度和最佳嵌岩深度的概念，并指出嵌岩深度对嵌岩桩桩端阻力的发挥有着显著的影响。刘树亚等[4]、宋仁乾等[7]、张建新等[10]通过现场试验和数值模拟等方法进一步证实了嵌岩桩的确存在最佳嵌岩深度，并分析了嵌岩深度对嵌岩桩承载特性的影响规律。同时，刘兴远等[5]基于BP网络模型，对表征嵌岩段特性的参数对嵌岩桩承载特性的影响进行了较为细致的讨论。纵观现有研究成果可以看出，嵌岩桩特性与其他类型桩基特性的根本差异来源于嵌岩桩嵌岩段特性的不同，且关于嵌岩特性对嵌岩桩承载及沉降特性的影响研究逐渐成为嵌岩桩研究的关键问题。

综上所述，关于嵌岩桩承载和沉降特性的研究已经相当广泛且深入，但关于动力荷载作用下嵌岩桩动力响应的研究仍较少。现有文献中，胡春林等[15]假定桩及其桩侧土为非线性弹性及线性粘弹性材料，对横向动荷载作用下嵌岩桩的动力特性进行了研究。李小彭等[16]借助ANSYS软件讨论了激振力幅值、频率以及土的刚度和阻尼对嵌岩桩沉桩速度和沉降量的影响。蔡邦国[17]结合现场试验，初步探讨了桩端沉渣对嵌岩桩动测信号的影响规律。进一步，王奎华等[18]采用虚土桩法模拟桩端沉渣对嵌岩桩的支承作用，得到了嵌岩桩桩顶速度频域响应解析解及相应的速度时域响应半解析解，并详细分析了沉渣特性对嵌岩桩桩顶动力响应的影响。尽管现有研究在嵌岩桩动力响应问题方面取得了一定成果，但总的说来仍没有完全揭示出嵌岩桩与土的动力相互作用机理。因此，为了提高嵌岩桩在受动荷载作用下的桥梁基础、海洋石油钻采平台基础及动力基础等工程中的设计水平，需进一步弄清动荷载作用下嵌岩桩的动力响应规律。

本文基于Novak等[19-20]、王奎华等[21]提出的平面应变振动模型来建立嵌岩桩桩侧土的控制方程，求得了考虑横向惯性效应时成层地基中嵌岩桩桩顶纵向振动阻抗在频域内的解析解，并详细讨论了嵌岩桩桩顶纵向振动阻抗的变化规律。

1 定解问题的建立

1.1 计算模型及假设条件

本文研究成层地基中任意纵向荷载作用下嵌岩桩的纵向振动问题，计算模型如图1所示。考虑桩侧土的成层性及嵌岩桩的变阻抗特性，将桩土系统从下至上划分为n个微元段，依次标识为1,2,…,j,…,n，各微元段的厚度依次为l1,l2,…,lj,…,ln，各微元段顶部深度分别为h1,h2,…,hj,…,hn，每一个微元段内桩材料和桩侧土为均质，桩段截面尺寸相同。H为嵌岩桩桩长，Hs为上覆土层厚度，Hb为嵌岩桩段的长度，rj为第j段桩身微元段截面半径。桩侧土采用平面应变模型，第j段桩侧土对该处桩身侧面单位面积作用力为fj(z,t)。

假设下列条件成立：

(1) 土层上表面为自由边界，无正应力和剪应力，嵌岩桩端部为刚性支承边界；

(2) 嵌岩桩为粘弹性、竖直的圆柱杆件，各桩段交界面之间完全连续接触；

(3) 桩土接触面上，土体动应力通过剪切复刚度传递给桩。

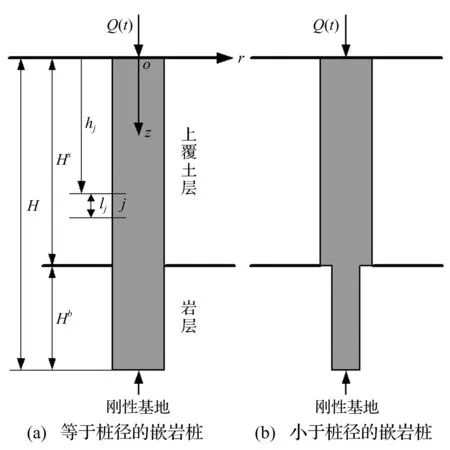
图1 计算模型

1.2 土体动力平衡方程

假设Wj=Wj(r)为第j层土体纵向振动的位移幅值，根据Novak等[19, 20]、王奎华等[21]提出的平面应变振动模型，土层的纵向振动平衡方程为：

(1)

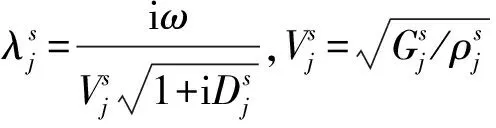
1.3 嵌岩桩纵向振动控制方程

黎正根等[22]、陈凡等[23]指出，应力波在大直径桩中传播时会因为频散效应而产生振荡现象，表现出显著的尺寸效应。而工程中的嵌岩桩通常长径比较小，采用传统的一维杆件振动模型来建立其纵向振动控制方程会存在一定的偏差。因此，为了考虑嵌岩桩的尺寸效应，同时也便于求解，本文采用Rayleigh-Love杆模型，即通过考虑嵌岩桩的横向惯性效应来近似考虑其尺寸效应。假设uj(z,t)为第j桩身微元段纵向振动的位移幅值，可建立基于Rayleigh-Love杆模型的嵌岩桩纵向振动控制方程如下：

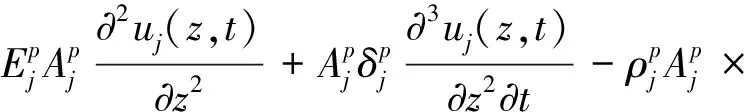
(2)

桩土系统振动过程中应满足如下边界条件和初始条件：

(1) 相邻嵌岩桩微元段分界面两侧的桩身位移和界面力满足连续条件，即：

uj(z,t)|z=hj=uj+1(z,t)|z=hj

(3)

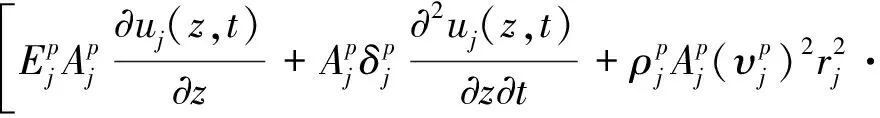
(4)

(2) 嵌岩桩桩顶及桩端处的边界条件：

(5)

u1(z,t)|z=H=0

(6)

(3) 振动开始时桩土系统满足的初始条件为：

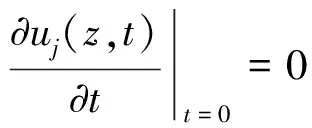
(7)

2 定解问题的求解

根据式(1)，结合Bessel函数理论，很容易得到第j层土体内任意一点土体的位移为：

(8)

式中：I0(λjr)和K0(λjr)分别为零阶第一类和第二类虚宗量Bessel函数，aj和bj为由边界条件确定的待定常数。根据平面应变模型的假设可知，土体水平无穷远处位移应力均衰减为0，结合Bessel函数性质可得bj=0。

根据弹性理论，可得土体内任意一点的纵向剪切应力为：

(9)

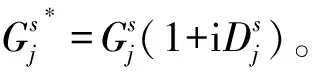
进一步，可以得第j微元段桩土接触面上单位长度方向的桩侧土作用在桩身的剪切复刚度为：

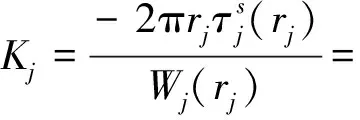
(10)

式中：K1(λjrj)为一阶第二类修正Bessel函数。

将式(10)代入式(2)，结合初始条件(7)，对嵌岩桩纵向振动控制方程两边进行Laplace变换并化简，可得：

(11)

由偏微分方程理论可得式(11)的解为：

(12)

(13)

根据阻抗函数的定义，可得第j微元段顶部(z=hj)界面处位移阻抗函数的解析表达式：

(14)

利用阻抗函数递推特性，通过式(14)进一步递推得到第n微元段顶部(即嵌岩桩桩顶)的位移阻抗函数：

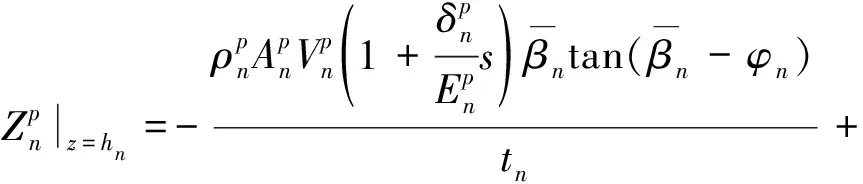
(15)

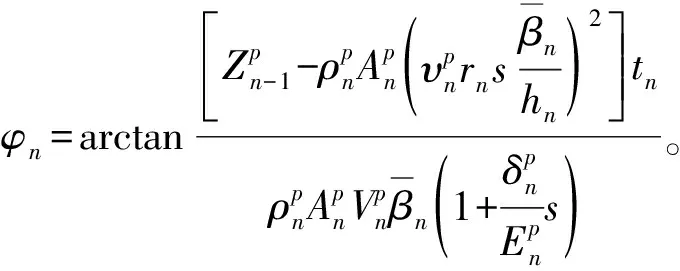
桩顶位移阻抗函数即桩顶复阻抗，实部代表了真实的动刚度，反映在弹性系统下，桩土系统抵抗纵向变形的能力，虚部代表动阻尼，反映了能量的耗散，将复阻抗表示成复数表达式如下：

(16)

3 嵌岩桩桩顶纵向振动阻抗分析

在文献[18]中，笔者通过将基于本文假设得到的桩顶时域曲线与现场采用低应变反射波法得到的实测曲线进行对比，验证了本文假设的合理性，因此，在此不对本文解的合理性做过多论述。刘兴远等[5]通过系统研究指出，嵌岩深度、桩径、岩层强度等参数对嵌岩桩承载特性具有重要影响。基于此，结合本文给出的解析解，详细讨论嵌岩深度、桩径、岩层强度等嵌岩特性对嵌岩桩桩顶纵向振动阻抗的影响。

3.1 嵌岩深度对桩顶纵向振动阻抗的影响分析

分2种情况讨论嵌岩深度对桩顶纵向振动阻抗的影响：① 上覆土层厚度不同时，通过逐步增大嵌岩深度来分析桩顶纵向振动阻抗的变化规律，并且随着嵌岩深度的增大，桩长不断增大；② 保持桩长不变，通过改变上覆土层厚度和嵌岩深度的值来分析桩顶纵向振动阻抗的变化规律。对于第一种工况，用于计算的参数为：上覆土层密度为2 000 kg/m3，剪切波速为150 m/s，厚度分别为Hs=10 m和Hs=20 m；岩层密度为2 100 kg/m3，剪切波速为280 m/s；桩身混凝土密度2 500 kg/m3，弹性纵波波速为4 000 m/s，桩身材料黏性阻尼系数为0，泊松比为0.25，嵌岩深度分别为Hb=0 m,1 m,3 m,5 m。

图2反映了在桩基础动力设计关注的低频范围内，不同上覆土层厚度时嵌岩深度对桩顶复阻抗的影响。由图2(a)可以看出，动刚度随着频率的增大先增大再减小。在同一频率处，动刚度随着嵌岩深度的增大而逐渐减小，且减小的幅度随着上覆土层厚度的增大而减小。对于同一嵌岩深度，上覆土层厚度越大，动刚度越小。由图2(b)可以看出，当频率超过5 Hz以后，动阻尼随着频率的增大基本呈现线性增大的趋势。随着嵌岩深度的增大，同一频率处的动阻尼也逐渐增大，但增大的幅度随着上覆土层厚度的增大而减小。对于同一嵌岩深度，上覆土层厚度越大，动阻尼也越大。这说明，对同一上覆土层厚度，嵌岩深度越大，在桩内传播的应力波的能量衰减越快。

图2 不同上覆土层厚度时嵌岩深度对桩顶复阻抗的影响

对于第二种工况，用于计算的参数为：桩长为20 m，上覆土层厚度分别为Hs=20 m,19 m,17 m,15 m，对应的嵌岩深度分别为Hb=0 m,1 m,3 m,5 m，其余参数与第一种工况的相应参数一致。

图3 桩长不变时嵌岩深度对桩顶复阻抗的影响

图3反映了在桩基础动力设计关注的低频范围内，桩长不变时嵌岩深度对桩顶复阻抗的影响。由图3(a)可以看出，在同一频率处，动刚度随着嵌岩深度的增大而增大。这说明，当桩长不变时，嵌岩深度越大，基桩抵抗纵向变形的能力越强。由图3(b)可以看出，当桩长不变时，嵌岩深度的变化对动阻尼的影响较小，基本可忽略。

3.2 桩半径对桩顶纵向振动阻抗的影响分析

分2种情况讨论桩径对桩顶纵向振动阻抗的影响：① 对于嵌岩桩段半径等于桩半径的嵌岩桩，分析不同嵌岩深度时桩半径对桩顶纵向振动阻抗的影响；② 对于嵌岩桩段半径小于桩半径的嵌岩桩，分析不同嵌岩深度时嵌岩桩段半径变化对桩顶纵向振动阻抗的影响。对于第一种工况，用于计算的参数为：上覆土层厚度为15 m，嵌岩深度分别为Hb=1 m和Hb=3 m，桩半径分别为rp=0.4 m,0.5 m,0.6 m,0.7 m，其余参数与4.1节第一种工况相应的参数一致。

图4 不同嵌岩深度时桩半径对桩顶复阻抗的影响

图4反映了在桩基础动力设计关注的低频范围内，不同嵌岩深度时桩半径对桩顶复阻抗的影响。由图4(a)可以看出，随着频率的增大，动刚度先增大再减小。在同一频率处，动刚度随着桩半径的增大而逐渐增大。对于同一桩半径，动刚度随着嵌岩深度的增大而逐渐减小，但减小的幅度随着桩半径的增大而增大。图4(b)可以看出，当频率超过5 Hz以后，动阻尼随着频率的增大基本呈现线性增大的趋势。在同一频率处，动阻尼随着桩半径的增大逐渐增大。这说明随着桩半径的增大，在桩内传播的应力波的能量衰减越快。由图4(b)还可以看出，对于同一桩半径，动阻尼随着嵌岩深度的增大而增大，且增大的幅度随着桩半径的增大而增大。

对于第二种工况，用于计算的参数为：定义嵌岩桩段与上覆土层桩段的半径比值为αr，通过αr的变化来反映嵌岩桩段半径的变化，αr越小，表示嵌岩桩段半径越小，其余参数与第一种工况相应的参数一致。

图5 不同嵌岩深度时嵌岩桩段半径对桩顶复阻抗的影响

图5反映了在桩基础动力设计关注的低频范围内，不同嵌岩深度时嵌岩桩段半径对桩顶复阻抗的影响。由图5(a)可以看出，在同一频率处，动刚度随着嵌岩桩段半径的增大而逐渐增大。对于同一嵌岩桩段半径，动刚度随着嵌岩深度的增大而逐渐减小，但减小的幅度随着嵌岩桩段半径的增大而增大。图5(b)可以看出，在同一频率处，动阻尼随着嵌岩桩段半径的增大逐渐减小，这是因为当嵌岩桩段半径较小时，相当于岩层填充了嵌岩桩段半径的减小部分，从而导致应力波的能量衰减加快。由图5(b)还可以看出，对于同一嵌岩桩段半径，动阻尼随着嵌岩深度的增大而增大，但增大的幅度随着嵌岩桩段半径的减小而增大。

3.3 岩层特性对桩顶纵向振动阻抗的影响分析

图6 岩层剪切波速对桩顶复阻抗的影响

图6反映了在桩基础动力设计关注的低频范围内，不同嵌岩深度时岩层剪切波速对桩顶复阻抗的影响。由图6(a)可以看出，在同一频率处，动刚度随着岩层剪切波速的增大而逐渐增大。对于同一岩层剪切波速，动刚度随着嵌岩深度的增大而逐渐减小，但减小的幅度随着岩层剪切波速的增大而减小。图6(b)可以看出，在同一频率处，动阻尼随着岩层剪切波速的增大逐渐减小，这表明随着岩层剪切波速的增大，桩内应力波能量衰减越慢。

4 结 论

本文通过综合分析嵌岩特性对桩顶复阻抗的影响，在桩基础动力设计关注的低频范围内得到如下结论：

(1) 对于同一上覆土层厚度，随着嵌岩深度的增大，同一频率处的动刚度逐渐减小，而动阻尼则逐渐增大，且动刚度和动阻尼变化的幅度均随着上覆土层厚度的增大而减小。当桩长不变时，增大嵌岩深度，可以增大动刚度，但对动阻尼的影响却较小。

(2) 对于嵌岩桩段半径等于桩半径的嵌岩桩，可以通过增大桩身截面半径来提高桩顶动刚度和动阻尼，但设计时要考虑嵌岩深度的影响。对于嵌岩桩段半径小于桩半径的嵌岩桩，桩顶动刚度随着嵌岩桩段半径的减小而减小，而动阻尼随着嵌岩桩段半径的减小而增大。

(3) 随着岩层特性变好，同一频率处的动刚度逐渐增大，但动阻尼逐渐减小。这说明，岩层特性越好，弹性条件下基桩抵抗动荷载引起的纵向变形的能力越强，而此时动荷载引起的应力波的能量衰减的越慢。

参 考 文 献

[1]Jonston I W, Lam T S K, Williams A F. Constant normal stiffness direct shear testing for socketed pile design in weak rock[J]. Geotechnique, 1987, 37(1): 83-89.

[2]黄求顺. 嵌岩桩承载力的研究[A]. 中国建筑学会地基基础学术委员会论文集[C]. 西安：陕西高校联合出版社，1992, 47-52.

[3]Zhang L Y, Herbert H E. End bearing capacity of drilled shafts in rock[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1998, 124(7): 547-584.

[4]刘树亚，刘祖德. 嵌岩桩理论研究和设计中的几个问题[J]. 岩土力学, 1999, 20(4): 86-92.

LIU Shu-ya, LIU Zu-de. Some problems on the research and design of rock-socketed piles[J]. Rock and Soil Mechanics, 1999, 20(4): 86-92.

[5]刘兴远，郑颖人. 影响嵌岩桩嵌岩段特性的特征参数分析[J]. 岩石力学与工程学报, 2000, 19(3): 383-386.

LIU Xing-yuan, ZHENG Ying-ren. Analysis on the parameters to affect behavior of rock-socketed segment of piles[J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(3): 383-386.

[6]邱钰，刘松玉，韦杰. 深长大直径嵌岩桩单桩沉降的简化计算[J]. 岩土工程学报, 2002, 24(4): 535-537.

QIU Yu, LIU Song-yu, WEI Jie. The simplified calculation of rock-socketed cast-in-site long piles with large diameter[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(4): 535-537.

[7]宋仁乾，张忠苗. 软土地基中嵌岩桩嵌岩深度的研究[J]. 岩土力学, 2003, 24(6): 1053-1056.

SONG Ren-qian, ZHANG Zhong-miao. Study on socket length length of rock-socketed piles in soft soil ground[J]. Rock and Soil Mechanics, 2003, 24(6): 1053-1056.

[8]董平，秦然，陈乾，等. 大直径人工挖孔嵌岩桩的承载特性[J]. 岩石力学与工程学报, 2003, 22(12): 2099-2103.

DONG Ping, QIN Ran, CHEN Qian, et al. Bearing behavior of large-diameter rock-socket piles[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(12): 2099-2103.

[9]赵明华，曹文贵，刘齐建，等. 按桩顶沉降控制嵌岩桩竖向承载力的方法[J]. 岩土工程学报, 2004, 26(1): 67-71.

ZHAO Ming-hua, CAO Wen-gui, LIU Qi-jian, et al. Method of determination of vertical bearing capacity of rock-socketed pile by the settlement of pile top[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(1): 67-71.

[10]张建新，吴东云，张淑朝. 嵌岩桩尺寸效应的有限元分析[J]. 岩土力学, 2007, 28(6): 1221-1224.

ZHANG Jian-xin, WU Dong-yun, ZHANG Shu-chao. Finite element analysis of size effect of rock-socketed piles[J]. Rock and Soil Mechanics, 2007, 28(6): 1221-1224.

[11]何思明，卢国胜. 嵌岩桩荷载传递特性研究[J]. 岩土力学, 2007, 28(12): 2599-2602.

HE Si-ming, LU Guo-sheng. Study on load transfer characteristic of rock-socketed pile[J]. Rock and Soil Mechanics, 2007, 28(12): 2599-2602.

[12]印长俊，王星华，夏力农. 大直径嵌岩桩残余应变状态分析[J]. 岩土力学, 2008, 29(11): 3095-3098.

YIN Chang-jun, WANG Xing-hua, XIA Li-nong. Analysis of residual strain state of large-diameter rock-socketed piles[J]. Rock and Soil Mechanics, 2008, 29(11): 3095-3098.

[13]赵明华，雷勇，刘晓明. 基于桩-岩结构面特性的嵌岩桩荷载传递分析[J]. 岩石力学与工程学报, 2009, 28(1): 103-110.

ZHAO Ming-hua, LEI Yong, LIU Xiao-ming. Analysis of load transfer of rock-socketed piles based on characteristics of pile-rock structural plane[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(1): 103-110.

[14]龚成中，龚维明，何春林，等. 孔壁粗糙度对嵌岩桩承载特性的影响[J]. 中国公路学报, 2011, 24(2): 56-61.

GONG Cheng-zhong, GONG Wei-ming, HE Chun-lin, et al. Influence of hole side roughness on bearing characteristic of deep rock-socketed pile[J]. Chinese Journal of Highway and Transport, 2011, 24(2): 56-61.

[15]HU Chun-lin, CHENG Chang-jun, HU Sheng-gang. Nonlinear dynamic characteristics of piles embedded in rock[J]. Journal of Shanghai University (English Edition), 2007, 11(3): 213-217.

[16]李小彭, 段泽亮, 李涛, 等.振动沉桩过程的动力学仿真分析[J]. 振动与冲击, 2012, 31(7): 24-26.

LI Xiao-peng, DUAN Ze-liang, LI Tao, et al. Dynamic simulation of a vibratory pile driving process[J]. Journal of Vibration and Shock, 2012, 31(7):24-26.

[17]蔡邦国，陈德银. 嵌岩桩桩底沉渣在桩基检测信号中的反映[J]. 土工基础, 2005, 19(5): 89-90.

CAI Bang-guo, CHEN De-yin. Reflection of residence around inserted pile bottom in pile foundation checking signals[J]. Soil Engineering and Foundation, 2005, 19(5): 89-90.

[18]王奎华，吴文兵，马少俊，等. 嵌岩桩沉渣特性对桩顶动力响应的影响[J]. 浙江大学学报(工学版), 2012, 46(3): 402-408.

WANG Kui-hua, WU Wen-bing, MA Shao-jun, et al. Influence of sediment characteristics on dynamic response at top of rock-socketed pile[J]. Journal of Zhejiang University (Engineering Science) , 2012, 46(3): 402-408.

[19]Novak M, Aboul-Ella F. Impedance functions of piles in layered media[J]. Journal of the Engineering Mechanical Division, ASCE, 1978, 104(EM3): 643-661.

[20]Novak M, Nogami T, Aboul-Ella F. Dynamic soil reaction for plane strain case[J]. Journal of the Engineering Mechanical Division, ASCE, 1978, 104(EM4): 953-959.

[21]吴文兵，王奎华，窦斌.任意层地基中粘弹性楔形桩纵向振动响应研究[J].振动与冲击, 2013, 32(8):120-127.

WU Wen-bing, WANG Kui-hua, DOU Bin. Vertical dynamic response of a viscoelastic tapered pile embedded in layered foundation[J]. Journal of Vibration and Shock, 2013, 32(8):120-127.

[22]黎正根, 龚育龄. 波在大直径桩中传播的三维效应现象[J]. 岩石力学与工程学报，1998，17(4)：434-439.

LI Zheng-gen, GONG Yu-ling. Discussion on three mensional effect of wave propagating in the pile with large diameter[J]. Chinese Journal of Rock Mechanics and Engineering, 1998, 17(4): 434-439.

[23]陈凡, 王仁军. 尺寸效应对基桩低应变完整性检测的影响[J]. 岩土工程学报，1998，20(5)：92-96.

CHEN Fan, WANG Ren-jun. Dimension effect on low strain integrity testing of piles[J]. Chinese Journal of Geotechnical Engineering, 1998, 20(5): 92-96.