基于波动法的复合材料圆柱壳阻尼特性分析

白宇杰，张小章

(清华大学 工程物理系，北京 100084)

复合材料具有比强度高、比刚度高和可设计性等优异性能，已经受到广泛应用，比如纤维缠绕成型的复合材料圆柱壳在高速旋转机械上的应用[1]。关于复合材料阻尼的研究进展，任勇生等[2]在2004年进行了总结，并用变分渐进法(Variational Asymptotical Method)对复合材料悬臂梁阻尼进行了分析[3]。Berthelot等[4-7]在2002年后针对复合材料单向板的阻尼做了系统的理论计算和实验验证。但关于复合材料圆柱壳的阻尼分析相对较少，阻尼分析在动力学研究的基础上进行，而这方面已经做了大量工作，如Lam等[8-10]采用四种不同的壳体理论比较了层合圆柱壳的固有频率，并研究了不同边界条件和铺层方式对振动的影响。Liew等[11]运用能量Ritz法研究了轴向加载旋转正交铺层圆柱壳的振动特性。很多研究者运用波动法对圆柱壳的动力学性能进行了研究，如Wang等[12]和Zhang等[13]采用波动法研究了有限长圆柱壳的共振频率，并与有限元方法的结果进行了比较。基于动力学研究，Alam等[14]用变分方法研究了径向简支复合材料圆柱壳的阻尼特性，Hufenbach等[15]用能量Ritz法进行了简支复合材料圆柱壳的阻尼分析。Saravanos等[16]开发了阻尼单元对悬臂情况下的复合材料圆柱壳阻尼进行了有限元分析。

由此可以看出，目前关于复合材料圆柱壳的阻尼分析，理论上仅限于简支边界条件，对于其余边界条件需要重新推导计算，过程冗繁，而有限元方法作为一种数值近似，计算成本较高，且对于阻尼预测缺乏实用性[3]。

本文运用波动法求解根据Love’s一阶壳理论得到的复合材料圆柱壳动力学方程，在振动分析的结果上建立了结构阻尼模型并进行了阻尼特性分析。波动法是求解圆柱壳动力学方程的一种计算方法[13]，可以方便地得到不同边界条件下的结果。与有限元方法相比，理论方法可以更方便地进行参数分析。本文针对简支(SS-SS)，悬臂(C-F)和固支(C-C)三种边界条件，从铺层角度和几何参数对复合材料圆柱壳的阻尼特性进行了分析研究。

1 振动方程

图1 复合材料层合圆柱壳动力学模型

复合材料层合圆柱壳模型示意图见图1，圆柱壳的厚度为h，半径为r，长度为L。采用曲面坐标系oxθz描述圆柱壳系统：u，v与w分别为圆柱壳在x，θ与z方向上的位移。基于Love’s理论，采用Hamilton原理建立复合材料层合圆柱壳的动力学方程[8]

(1)

其中Lij(i,j=1,2,3)是微分算子。壳体的位移函数可以表示为波动的形式：

(2)

式中:Umn，Vmn，Wmn分别为3个坐标方向上的波幅；ω为角频率；t为时间；km为轴向波数，n为环向波数。将式(2)代入式(1)得

(3)

其中Cij(i,j=1,2,3)是系数。式(3)有非零解的条件是系数矩阵的行列式为0，即

(4)

将式(4)展开，得到关于圆柱壳周向波数、环向波数和频率的特征方程

f(km,n,ω)=0

(5)

利用该方程就可以分析复合材料圆柱壳的振动特性，其中关键一步就是根据壳体的边界条件选取相同边界条件下梁的波数作为壳体的轴向波数[7]，环向波数根据分析的振型进行选取，然后就可以得到关于频率ω的6次方程

ω6+b4ω4+b2ω2+b0=0

(6)

其中bi(i=4,2,0)是方程系数。求解式(6)得到3个根，分别对应于壳体在3个方向上的振动频率，其中最低频率对应弯曲振动，另外的频率对应壳体的面内振动。得到相应轴向波数和环向波数下的振动频率后，代入式(3)可以求解振幅之间的关系，进一步得到相应的位移函数。本文讨论最低频率即一阶弯曲振动的情况。

2 阻尼模型

图2 复合材料层合圆柱壳截面模型

复合材料层合圆柱壳的截面模型如图2所示。假设各层复合材料都是正交各向异性，则考虑第k层的应变能为[7]

(7)

其中:

(8)

根据复合材料本构关系可得主轴方向应力应变为

(9)

其中各折减刚度系数为

Q12=Q21=νLTQ22,Q66=GLT

利用式(9)将式(8)改写为

柳含烟认为萧飞羽不仅搞错了当初在马车上露脸的是谁，从那“傲慢得要命的丫头”该是唤起的模糊印象也是她多么年幼无知，以致错上加错搞混了她和白雪，又由于为她解穴时发现她非处子才说：“如果你不是名花有主我一定不会放过你。”也因为他认为她稚气无知才会有意外的言词，并把她如此模样摆在腿上欣赏。她温顺地道：“含烟满足您心疼含烟，也会努力使您信任含烟。”萧飞羽凝视柳含烟，目光渐渐深邃，以致柳含烟觉得那目光透过她的双眸看到了她的心扉，心也紧张得像小鹿一样“砰砰”乱跳，因为她认为她真的唤起了他疼爱她，所以他正在思索如何犒赏年幼无知的她。也非常担心她“名花有主”也不放过她。

(10)

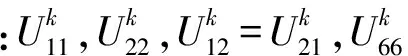
实际计算得到的应变在偏轴方向，将主轴方向上的应变转换为偏轴方向上得

(11)

其中l=cosθ,m=sinθ。将式(11)中的主轴应变代入式(10)中可得应变能与相应振型的应变之间的关系。

式(11)中的偏轴应变可以根据Love’s假设得到

(12)

其中:ε1,ε2,ε12是参考面应变，k1,k2,τ是参考面曲率的变化，它们的定义如下:

将振型函数式(2)代入其中即可得偏轴应变，进一步可得主轴应变，进而得到应变能。

则有

第k层的应变能为

(13)

于是得到第k层由于阻尼耗散的能量为

(14)

其中:η11,η22分别是纤维纵向和横向上面的拉压阻尼损耗因子，η12是面内耦合损耗因子，η66是面内剪切损耗因子，进一步可以求得整体的损耗因子为

η=∑ΔUk/∑Uk

(15)

3 结果讨论

为了检验本文建立的阻尼模型及其近似计算方法的正确性，表1给出了两种CUS构型，即沿薄壁圆柱壳轴线的铺层方式分别为[0]16和[90]16，的复合材料圆柱壳在悬臂梁边界条件下的一阶弯曲模态频率和阻尼计算结果，并且与文献[16]中的剪切梁阻尼的有限元结果进行了比较，结构的几何参数和材料参数均取自文献[16]。表1中文献[16]的结果中左边表示Beam FE结果，右边表示Damped shell FE结果。可以看出，本文结果和文献中符合得很好。

基于上述分析，本文针对简支(SS-SS)，悬臂(C-F)和固支(C-C)三种边界条件，探讨[0/θ2/90]和[±θ]2铺层下铺层角度和几何参数对复合材料圆柱壳的阻尼特性的影响，以下是各边界条件对应的轴向波数：

简支-简支(SS-SS)：sin(kmL)=-1；

固定-自由(C-F)：cosh(kmL)=cos(kmL)=-1；

固定-固定(C-C)：cosh(kmL)=cos(kmL)=1。

圆柱壳的几何参数如下：圆柱壳中面直径为d=352 mm，壁面厚度h与圆柱壳长度L是与d成比例的参数。复合材料的材料参数如表2所示。

表1 复合材料圆柱壳的模态阻尼和频率中面半径d=352 mm，壳体厚度h=10.16 mm

表2 复合材料性能参数

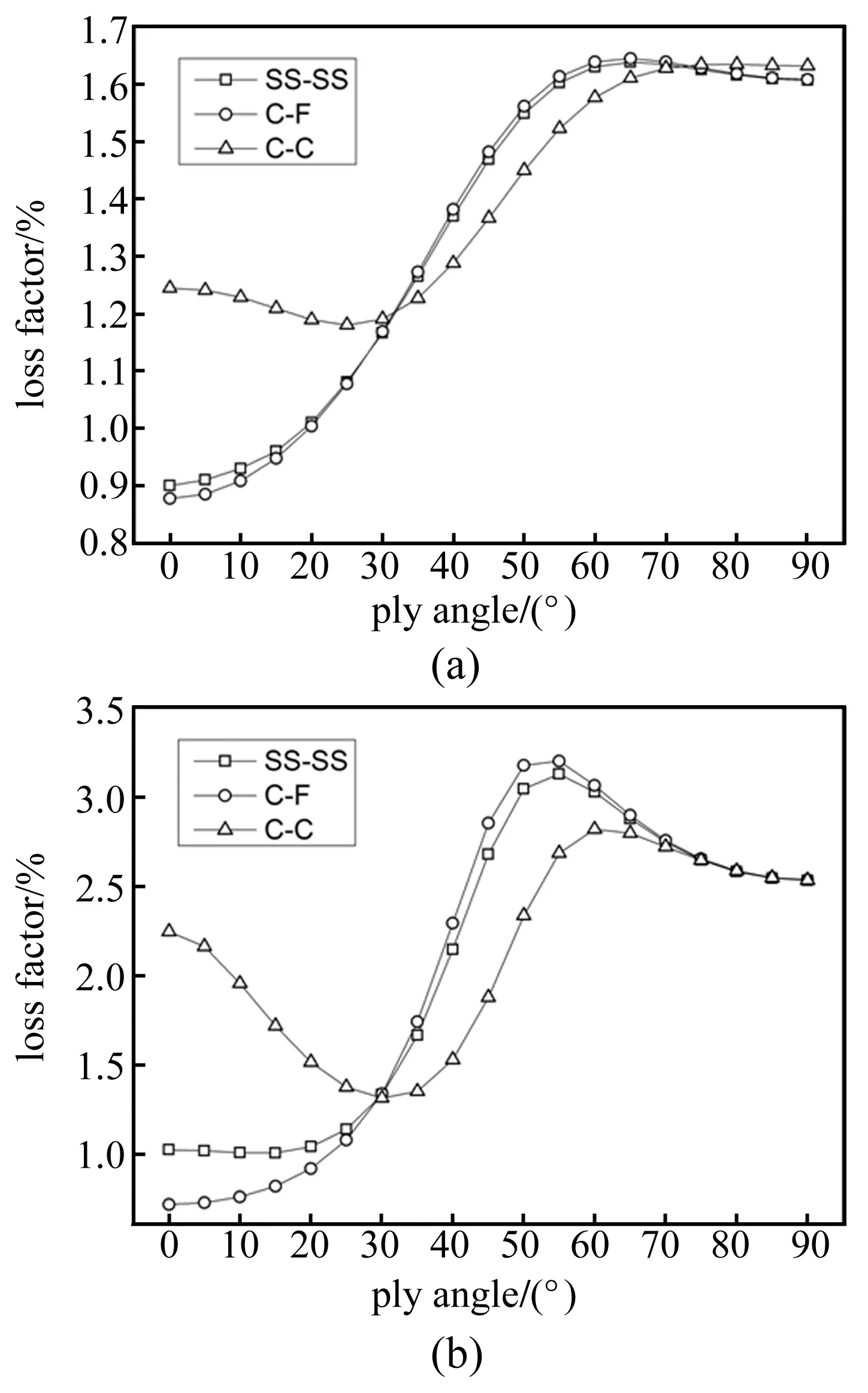
图3 不同边界条件下[0/θ2/90](a)和[±θ]2(b)铺层圆柱壳第一阶弯曲模态阻尼随铺层角度的变化曲线(L/d=10，h/d=0.01)

图3表示复合材料圆柱壳在不同边界条件下的第一阶弯曲模态阻尼随铺层角度的变化曲线。结果(a)和(b)表明，对于简支和悬臂边界条件，第一阶弯曲模态的阻尼在铺层角度为0°～30°时平缓增加，在30°～60°时剧烈增加，在60°～90°时有一定下降，最大的阻尼发生在铺层角度为50°～60°的区间，最大的阻尼是最小阻尼的2～3倍；对于固支边界条件，唯一不同是第一阶弯曲模态的阻尼在0°～30°之间减少，直至三条线交于30°。由于面内剪切损耗因子和横向拉压损耗因子的影响较大，因此当模态中剪切和横向拉压作用较大时，相应的模态损耗因子就会较大，因此图中最大损耗因子出现在60°左右，这也解释了(b)的损耗因子大于(a)的原因。根据图3，在相同的几何及[0/θ2/90]和[±θ]2的铺层条件下，约束较弱的边界条件对应的模态阻尼在不同的角度下表现不同，如0°～30°和60°～90°范围内约束越弱则损耗因子越小，30°～60°范围内约束越弱则损耗因子越大。

图4 不同边界条件下铺层圆柱壳第一阶弯曲模态阻尼随长径比的变化曲线([0/452/90](a)[±45]2(b)，h/d=0.01)

图4表示复合材料圆柱壳在不同边界条件下的第一阶弯曲模态阻尼随长径比L/d的变化曲线。结果(a)和(b)表明，对于图中所示的边界条件，第一阶弯曲模态的阻尼随着长径比L/d的增大而增大，最终趋于一致。在长径比1

图5表示复合材料圆柱壳在不同边界条件下的第一阶弯曲模态阻尼随厚径比h/d的变化曲线。结果(a)表明，对于图中所示的边界条件，第一阶弯曲模态的阻尼随着厚径比h/d的增大而增大；与(a)相比，(b)中模态阻尼随着厚度的增加并不明显。由于厚度增加引起了剪切作用的增加，因此模态损耗因子自然增加。根据图5，在相同的几何及铺层条件下，约束较弱的边界条件对应的模态阻尼较大，这是因为铺层角度[0/452/90]和±45]2以及长径比L/d=20的选择都在约束越弱则损耗因子越大的范围内。

图5 不同边界条件下铺层圆柱壳第一阶弯曲模态阻尼随厚径比的变化曲线([0/452/90](a),[±45]2(b),L/d=20)

4 结 论

本文基于Love’s一阶壳理论，运用波动法建立了复合材料圆柱壳结构阻尼分析模型。研究表明，采用本文建立的解析模型和计算方法所获得的复合材料圆柱壳模态阻尼和固有频率数值解，与已有的有限元结果基本一致。针对简支(SS-SS)，悬臂(C-F)和固支(C-C)三种边界条件，对[0/θ2/90]和[±θ]2铺层复合材料圆柱壳的阻尼特性的分析表明：

(1)根据本文模型能够对复合材料圆柱壳的结构阻尼性能进行参数分析，确定影响圆柱壳阻尼特性的主要因素，为进一步改善圆柱壳的阻尼耗散性能提供有用的信息。

(2)纤维铺层角度，长径比和厚径比对圆柱壳的结构阻尼能够产生显著的影响。对于本文中的弯曲模态，结构阻尼基本随着角度的增大先增大后减小，在60°左右达到最大；随着长径比的增大而增大，在30°左右趋于一致；随着厚径比的增大一直增大。

(3)边界条件对复合材料圆柱壳的阻尼特性有一定的影响。在相同的铺层角度和几何条件下，约束的强弱对结构阻尼也会产生影响。如在铺层角度为30°～60°，长径比1～30范围内，约束越弱则阻尼越大。

[1]Werner S.Vibrations of shells and Plates [M].2 ed.CRC Press,1993.

[2]任勇生,刘立厚.纤维增强复合材料结构阻尼研究进展[J].力学与实践，2004，26(1):9-16.

REN Yong-sheng，LIU Li-hou.Advances in damping analysis and design of fibre reinforced composite material structures [J].Mechanics in Engineering，2004，26(1):9-16.

[3]任勇生,杜向红,孙双双,等.单闭室复合材料薄壁梁的结构阻尼[J].振动与冲击，2012，31(3):141-146.

REN Yong-sheng，DU Xiang-hong，SUN Shuang-shuang，et al .Structural damping of thin-walled composite one-cell beam [J].Journal of Vibration and Shock，2012，31(3):141-146.

[4]Berthelot J M，Sefrani Y.Damping analysis of unidirectional glass and Kevlar fibre composites[J].Composites Science and Technology，2004(64):1261-1278.

[5]Berthelot J M.Damping analysis of laminated beams and plates using the Ritz method[J].Composite Structures，2006(74):186-201.

[6]Berthelot J M，Sefrani Y.Longitudinal and transverse damping of unidirectional fibre composites[J].Composite Structures，2007(79):423-431.

[7]Berthelot J M，Assarar M，Sefrani Y，et al.Damping analysis of composite materials and structures[J].Composite Structures，2008(85):189-204.

[8]Lam K Y，Loy C T.Analysis of rotating laminated cylindrical shells by different thin shell theories [J].Journal of Sound and Vibration,1995,186(1):23-35.

[9]Lam K Y，Loy C T.Influence of boundary conditions and fibre orientation on the natural frequencies of thin orthotropic laminated cylindrical shells[J].Composite Structures,1995,31: 21-30.

[10]Lam K Y，Loy C T.Influence of boundary conditions for a thin laminated rotating cylindrical shell [J].Composite Structures,1998,41:215-228.

[11]Liew K M，Ng T Y，Zhao X.Vibration of axially loaded rotating cross-ply laminated cylindrical shells via ritz method [J].J.Eng.Mech，2002,128:1001-1007.

[12]Wang C，Lai J C S.Prediction of natural frequencies of finite length circular cylindrical shells [J].Applied Acoustics,2000，59:385-400.

[13]Zhang X M，Liu G R，Lam K Y.Vibration analysis of thin cylindrical shells using wave propagation approach [J].Journal of Sound and Vibration，2001，239 (3):397-403.

[14]Alam N，Asnani N T.Vibration and damping analysis of a multilayered cylindrical shell，Part I theorical results[J].AIAA Journal，1984，22(6):803-810.

[15]Hufenbach W，Holste C，Kroll L.Vibration and damping behaviour of multi-layered composite cylindrical shells[J].Composite Structures,2002,58:165-174.

[16]Saravanos D A，Varelis D，Plagianakos T S，et al.A shear beam finite element for the damping analysis of tubular laminated composite beams[J].Journal of Sound and Vibration，2006，291:802-823.