一维嵌套结构声子晶体透射特性

胡家光， 徐 文， 邱学云

(1.文山学院 数理系，云南 文山 663000； 2.云南大学 物理科学技术学院，昆明 650091)

周期性功能材料作为感兴趣的研究对象， 由半导体材料器件到光子晶体均已取得巨大成就。近年来又提出声子晶体概念。与光子晶体结构类似，声子晶体为由不同弹性材料周期性排列而成的复合功能材料，理论、实验均证明，在适当条件下，弹性波在声子晶体中传播时会产生与光子晶体相似的禁带[1-3]。声子晶体中存在缺陷时带隙内产生局域模，带隙内弹性波只能被局限在缺陷处或沿缺陷传播[4]。声子晶体禁带特性及局域模使其在减振降噪及声学功能器件领域应用前景广阔[5]。与光子晶体不同，电磁波只有横波，而弹性波在不同介质中传播时偏振状态会不同，在流体中传播时只有纵波，而在固体中传播时有横波亦有纵波，亦可能存在纵波与横波耦合，故声子晶体带隙的获取及计算更复杂，尤其超低频带隙的获取更具挑战性。

在声子晶体研究中，一维声子晶体因其制作简单，体积小，带隙易控制备受关注[6-7]。一般情况下声子晶体带隙越宽，应用价值越高。为获得更理想带隙特性，在简单晶格基础上，将Fibonacci、Thue-Morse、功能梯度及无序等结构引入一维声子晶体中[8-12]。而该新型结构拓宽声子晶体带隙效果并不显明，且局域模调控性亦不理想。因此，探索拓宽一维声子晶体带隙方法及研究调控局域模手段尤其重要。本文进行过大量探索研究，发现可大幅拓宽一维声子晶体带隙的周期嵌套结构，并借助掺杂作用，可较好实现局域模的调控，并对其中机理进行详细阐述。

1 模型及计算方法

设计多种类型一维周期嵌套结构，最佳组合形式见图1，结构共j层。将一个周期称复周期，由A、B、C、D四部分组成，晶格常数为a。图1中黑色部分A及C表示同一种材料，灰色部分B及D表示另一种材料，四部分厚度分别为d1、d2、d3、d4，整结构由N个复周期排列而成，入射、出射端材料相同用E表示。若d1=d3及d2=d4，则变为晶格常数为a/2的简单晶格结构。研究重点为d1≠d3及d2≠d4情形，该声子晶体也可视为由周期单元A+B及C+D的两套声子晶体嵌套而成，在此结构中已发现非常有价值结果。为便于计算，令L1=d1+d2、L2=d3+d4、T1=d1/d2、T2=d3/d4、T3=L2/L1。

图1 一维复周期声子晶体结构模型

为准确研究此类结构声子晶体带隙特性，本文用传递矩阵法计算[13-14]，研究纵波及横波垂直入射时的透射率。在此条件下，不存在横波与纵波的转型问题。据纵波及横波在晶体中传播时边界条件，可得纵横波位移波矢在两种介质界面处共同的传递矩阵Mpq=M-1PM-1q。其中Mp及Mq为相邻第p、第q层介质系数矩阵，可统一下标p定义为：

(1)

式中：kL=ω/cL；kT=ω/cT；cL，cT分别为纵波波速及横波波速；ω为圆频率；λ，μ为拉密常数。弹性波经厚度dp的介质p时传递矩阵为：

(2)

弹性波通过整个声子晶体时，总传递矩阵为：

W=M01N1M12N2…Mj0

(3)

由此可得纵波透射率TL及横波透射率TT为：

(4)

选常用材料钢与环氧树脂构成声子晶体,入射及出射端材料选有机玻璃,材料参数见表1,复周期数为10,缺陷层材料铅后续。

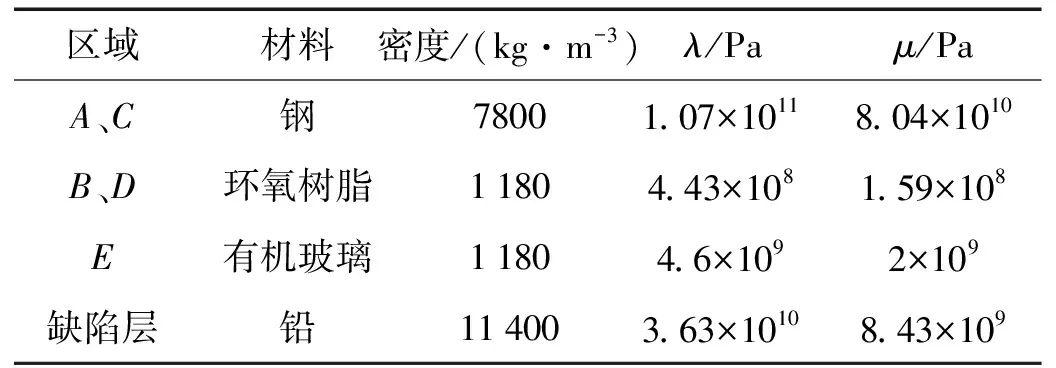
表1 材料物理参数

2 结果与讨论

计算复周期结构与简单晶格结构带隙差异，选复周期结构参数a=3 cm，T1=T2=1，T3=2。为使比较具合理性，简单晶格结构由相同材料钢及环氧树脂组成，厚度比取1，晶格常数a取3 cm。结果见图2，纵坐标为波透射率，相邻透射谱线间空白区域为带隙；横坐标为波频率f。为能更全面反映带隙情况，频率f取值范围较宽。

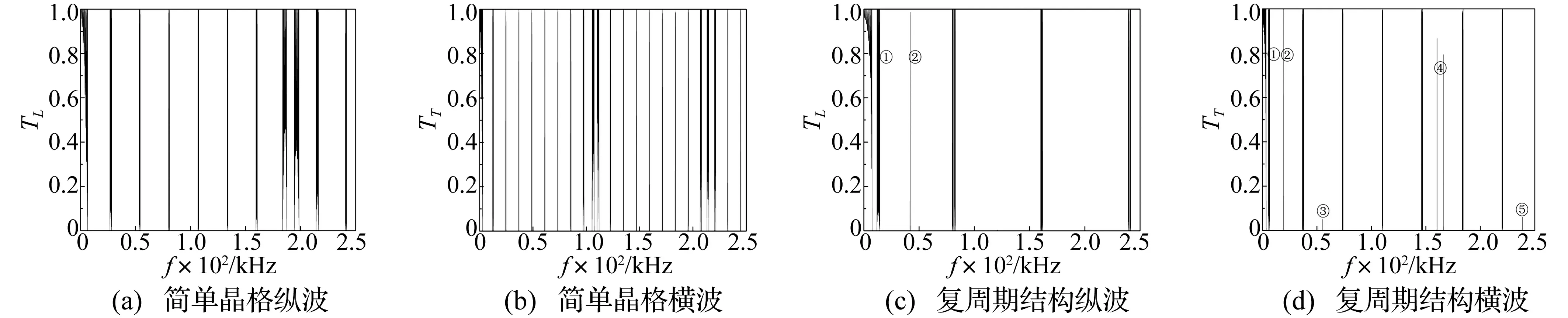
图2 透射率谱图(a=3 cm, T1= T2=1, T3=2)

对比图2(a)、图2(c)看出，简单晶格透射谱线较密集，带隙宽度较小，从左至右，前6个带隙宽度近似相等，约25 kHz。而复周期结构透射谱线较稀疏，故带隙被极大拓宽，第二、三带隙宽度达80 kHz，为简单晶格结构的3.2倍，称为巨带隙，在更高频率区亦有类似现象。其机理可解释为，相比简单周期，波在一个复周期内传播时受到更复杂周期内部调制，该调制在多层复周期结构中均有作用，但否能产生宽带隙，与材料弹性常数、层数及各层厚度密切相关，见式(2)、式(3)。而用复周期结构，调整适当参数，确可获得较简单周期宽数倍的巨带隙，此为声子晶体应用提供了新设计思路。此外，该结构可视为由两套晶格常数不同的简单晶格声子晶体嵌套而成，晶格常数不同的声子晶体带隙结构差异较大，在某些参数下，不同晶格引起的布拉格反射效应发生作用会增大带隙。该嵌套叠加结构与将多组声子晶体按顺序复合效果[15]不同，按顺序复合时波总的传递矩阵可视为各组声子晶体传递矩阵顺序叠加。而本文结构中波总的传递矩阵可视为两套声子晶体各层传递矩阵元的嵌套叠加，数学上获得两种不同的传递矩阵值，导致不同带隙结构。对比图2(b)、图2(d)，复周期结构中横波带隙远宽于简单晶格结构横波带隙，但横波带隙较结构中纵波带隙小很多，主要因为横波波长较短，满足布拉格带隙弹性波频率下降所致。 除带隙变宽外，图2(c)、图2(d)中亦出现类似缺陷体的局域模，图2(c)中仅在第一带隙内出现两个局域模。将其放大发现，局域模①较宽，频率范围10.5～14.3 kHz，呈类周期振荡形态，其透射率峰值为1，表明该频率范围内波较容沿此局域模透过整个声子晶体。而局域模②较陡峭，透射率峰值为0.98。图2(d)中，除①、②两局域模与图2(c)类似外，在第二、五、七个带隙内均出现局域模，但③、⑤两模的透射峰极小，意义不大。复周期结构出现局域模原因可解释为两套周期间互为准缺陷，将此种作用称准缺陷耦合。准缺陷耦合不但产生传统缺陷的局域模，亦放大(在某些参数条件下也可能缩小)纵波及横波中局域模①的范围，且可获得较高透射率。

晶格常数a及T1，T2，T3与带隙关系见表2。巨带隙易出现在T1>1时，T2及T3主要影响缺陷模的位置与数量，而a对带隙宽度、位置及局域模均有影响。图3为T1>1时，T2=0.5<1及T2=2>1两种情况纵波透射率谱图。与图2(c)对比，图3(a)、图3(b)中纵波带隙范围进一步拓宽，但T2<1时，第一带隙内局域模数量增加；T2>1时，第一带隙内除局域模①外，其余局域模消失，转而出现在第二带隙内。横波变化亦相似。由此可见，复周期结构可提供更多可调节结构参数，更易实现对带隙及局域模调控。

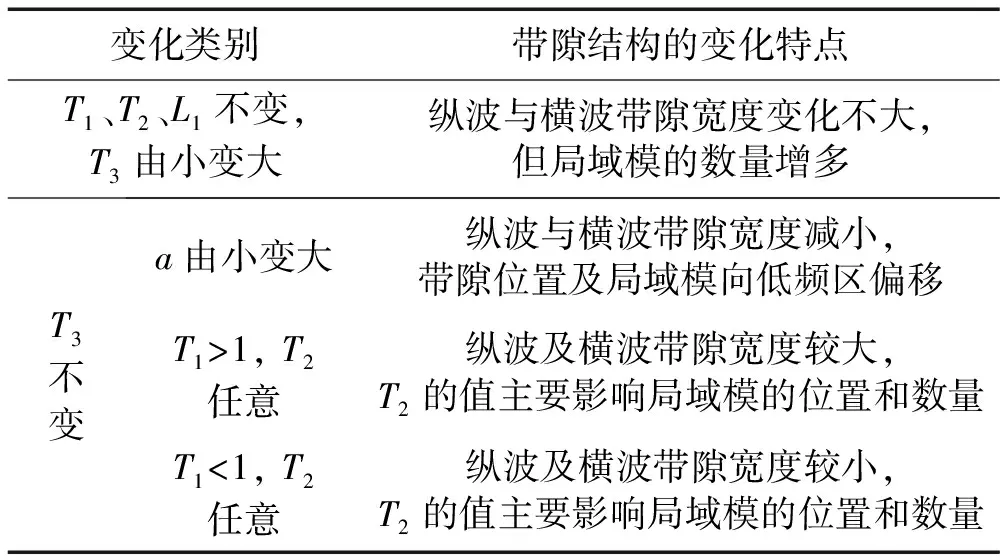
表2 结构参数对带隙影响

局域模始终伴随各结构参数变化出现，为声子晶体在波导领域的应用提供了可能。但局域模也会对声子晶体滤波效应产生干扰，尤其低频区局域模①因其宽度较大，且始终存在，会严重影响声子晶体低频滤波效应，若能针对性控制局域模，会更有利于声子晶体在器件中应用。因此本文探讨多种方法调控局域模，发现在复周期间插入另一缺陷层方法最有效，缺陷层位置及厚度对局域模会产生极大影响。选择高密度铅材料为缺陷层，物理参数见表1，缺陷层位于第一～第九个复周期后某位置。局域模①透射率极值与缺陷层位置及厚度关系见图4，横坐标为缺陷层厚度D与d1的比值，d1及其它结构参数值同图2。很明显，纵波与横波局域模①的透射率极值均随缺陷层厚度的增加而减小，尤其缺陷层位于1、3、7、9复周期后时，透射率极值远小于其它位置。D/d1=3时，在四位置上纵波与横波局域模①的透射率极值约0.02，基本可忽略局域模①的影响，对扩大声子晶体在低频范围内的应用具有重要意义。

在第一复周期后插入缺陷层时纵波及横波第一带隙谱见图5，D/d1=3，与图2(c)、图2(d)相比，缺陷层引入最明显为基本消除了纵波及横波中局域模①、②，带隙变宽及更连续。第一带通区随频率的增大，透射率振荡呈较大衰减，第二带通区透射峰值有一定程度下降，横波变化较纵波更显著。更高频率局域模及带通区变化亦相似。研究结果表明，通过改变缺陷层位置及厚度可有效控制局域模的产生及消失。其机理可从两方面解释，由数学角度，引入缺陷层可通过缺陷矩阵实现，缺陷层位置或厚度不同时，缺陷矩阵在总传递矩阵中位置或数值亦不同。由于矩阵运算不满足交换律，故所得结果不同。由物理角度分析，缺陷层的引入会产生自己局域模，新局域模与原准缺陷耦合产生的局域模相互作用降低(在某些参数条件下可能增强)某些局域模透射率，将此作用称缺陷共振，缺陷共振的强弱与新局域模位置及强度密切相关，而新局域模主要由缺陷层厚度及位置决定，故得出上述结果。

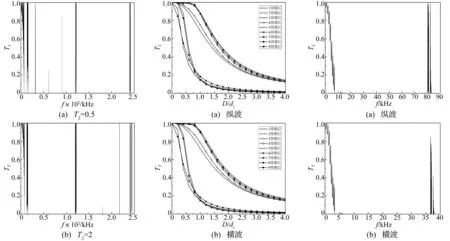
图3 纵波透射率谱图(a=3 cm, T3=T1=2)

3 结 论

(1) 本文通过将周期嵌套结构引入一维声子晶体中,推导出该结构的传递矩阵、计算其带隙特性,获得透射率谱图。

(2) 通过内周期对波的调制作用,获得较传统简单晶格结构宽数倍的巨带隙,且同时存在于纵波及横波中。带隙中横波局域模多于纵波局域模。巨带隙易在T1>1时出现,而T2、T3主要影响缺陷模位置及数量, 而a对带隙宽度、位置及局域模均有影响。

(3) 通过在复周期间掺入缺陷层铅,发现纵波与横波局域模透射率极值均随缺陷层厚度的增加而减小，并提出缺陷共振机理,将有助于增强声子晶体低频滤波效应。

(4) 本文一维周期嵌套结构无论在宽带隙获取,或局域模及调控性均优于已有研究结论。此类声子晶体应用前景会更好。

参 考 文 献

[1]Lu M H, Liang F, Chen Y F. Phononic crystals and acoustic metamaterials[J]. Materials Today, 2009, 12(12): 34-42.

[2]Merkel A, Tournat V, Gusev V. Experimental evidence of rotational elastic waves in granular phononic crystals[J]. Physical Review Letters, 2011, 107(22):225502-1-225502-5.

[3]Wang Y F, Wang Y S, Su X X. Large bandgaps of two-dimensional phononic crystals with cross-like holes [J]. Journal of Applied Physics, 2011, 110(11): 113520-1-113520-13.

[4]Su X X, Wang Y F, Wang Y S. Effects of Poisson's ratio on the band gaps and defect states in two-dimensional vacuum/solid porous phononic crystals [J]. Ultrasonics, 2012, 52(2): 255-265.

[5]Pennec Y, Vasseur J O, Djafari-Rouhani B, et al. Two-dimensionalphononic crystals:examples and applications[J]. Surface Science Reports, 2010, 65(8): 229-291.

[6]舒海生, 刘少刚, 王威远, 等. 集中质量边界条件下声子晶体杆的纵向振动传递特性研究[J]. 振动与冲击, 2012, 31(19): 113-117.

SHU Hai-sheng, LIU Shao-gang, WANG Wei-yuan, et al. Transmission characteristics of longitudinal vibration of a phononic crystal rod with concentrated mass boundary condition [J]. Journal of Vibration and Shock, 2012, 31(19): 113-117.

[7]迟乾坤, 温激鸿, 郁殿龙. 弹性地基上具有轴向载荷的充液周期管弯曲振动带隙研究[J]. 振动与冲击, 2012, 31(18): 128-131.

CHI Qian-kun, WEN Ji-hong, YU Dian-long. Band gap of flexural vibration of a periodic pipe conveying fluid with axial forces on an elastic foundation [J]. Journal of Vibration and Shock, 2012, 31(18): 128-131.

[8]曹永军, 董纯红, 周培勤. 一维准周期结构声子晶体透射性质的研究[J]. 物理学报, 2006, 55(12): 6470-6475.

CAO Yong-jun,DONG Chun-hong,ZHOU Pei-qin. Transmission properties of one-di-mensional qusi-periodical phononic crystal[J]. Acta Physica Sinica,2006,55(12):6470-6475.

[9]杨立峰, 王亚非, 周 鹰. 一维压电Fibonacci类准周期声子晶体传输特性[J]. 物理学报, 2012, 61(10): 107702-1-107702-6.

YANG Li-feng, WANG Ya-fei, ZHOU Ying. The transmission properties in one-dimensional piezoelectric fibonacci-class quasi-periodical phononic crystals [J]. Acta Physica Sinic, 2012, 61(10): 107702-1-107702-6.

[10]曹永军, 杨 旭, 姜自磊. 弹性波通过一维复合材料系统的透射性质[J]. 物理学报, 2009, 58(11): 7735-7740.

CAO Yong-jun, YANG Xu, JIANG Zi-lei. Transmission property of elastic wave through one-dimensional compound materials [J]. Acta Physica Sinica, 2009, 58(11): 7735-7740.

[11]Wu M L, Wu L Y, Yang W P, et al. Elastic wave band gaps of one-dimensional phononic crystals with functionally graded materials[J]. Smart Materials and Structures, 2009, 18(11): 115013-1-11513-8.

[12]Chen A L, Wang Y S. Study on band gaps of elastic waves propagating in one-dimensional disordered phononic crystals [J]. Physica B, 2007, 392(1-2): 369-378.

[13]Luan P G, Ye Z. Acoustic wave propagation in a one-dimensional layered system [J]. Physical Review E, 2001, 63(6): 066611-1-066611-8.

[14]刘启能. 弹性波斜入射声子晶体的传输特性[J]. 应用力学学报, 2009, 26(2): 397-400.

LIU Qi-neng. Transfer characteristic of phononic crystal during elastic wave oblique incidence [J]. Chinese Journal of Applied Mechanics, 2009, 26(2): 397-400.

[15]曾广武, 肖 伟, 程远胜. 多组声子晶体复合结构的隔声性能[J]. 振动与冲击, 2007, 26(1): 80-83.

ZENG Guang-wu, XIAO Wei, CHENG Yuan-sheng. Sound isolation of composite structure consisting of multiphononic crystals [J]. Journal of Vibration and Shock, 2007, 26(1): 80-83.