Q345等边角钢腐蚀疲劳性能试验研究

张春涛， 范文亮， 李正良

(1 西南科技大学 土木工程与建筑学院，四川 绵阳 621010；2 重庆大学 土木工程学院，重庆 400045)

由于疲劳损伤的随机性，传统疲劳试验研究中需据大子样试验数据推断试件的疲劳统计特性。文献[1]建议测定材料疲劳性能时用成组法及升降法，成组法测定P-S-N曲线时至少需测试3级疲劳应力水平共计24个试件，测试疲劳极限或条件疲劳极限的升降法则需用30个试件。成组法不仅需试件数量多，且测量精度低，尤其在测定高可靠度、高置信水平的P-S-N曲线时耗时久、耗费大，工程上难以接受。为减少试件、缩短时间，文献[2-3]结合极大似然法推荐仅需14个试件即能测定S-N曲线的单点-成组法；Ling等[4]在三参数幂函数基础上结合极大似然法提出更实用的测定P-S-N曲线的改进单点-成组法；但单点-成组法所需试件仍较多，且仅少量试件用于测定曲线。为克服此不足，傅惠民[5-7]通过对a-N曲线及ε-N曲线三参数幂函数拟合方法研究，给出既节省试件又具较高精度的回归分析法；熊俊江等[8-9]据定量方程随机化方法建立只需单点试验而无需成组试验即能测定P-S-N曲线的单点-似然法；但该方法在确定系数数值求解过程中，每次迭代计算均需假定其它各参数值并参与计算，计算量大、过程繁琐。由于试验条件及经费等限制，与试验理论快速发展相比，对构件疲劳性能试验研究匮乏，而与材料疲劳性能相比，构件疲劳性能受截面形式、应力分布、边界条件等影响存在较大差异。结构体系中构件长期受环境、大气等腐蚀介质浸蚀致使构件截面尺寸减小、疲劳性能退化，使构件腐蚀疲劳性能研究更复杂。为此本文在引入相关系数优化法改进单点-似然法基础上建立腐蚀疲劳t-P-S-N曲面模型；通过三组不同腐蚀时间18根足尺试件研究Q345等边角钢构件的腐蚀疲劳破坏特征，并由试验结果建立Q345等边角钢试件的t-P-S-N曲面模型。

1 腐蚀疲劳t-P-S-N曲面方程式建立

1.1 基于单点-似然法参数回归分析

中长寿命区S-N曲线常用三参数幂函数表示：

(S-S0)mN=C

(1)

式中：S0，m，C均为材料常数。相同腐蚀条件下材料疲劳性能随腐蚀时间t出现退化，式(1)可表示为：

[S-S0]m(t)N=C(t)

(2)

由式(2)看出，材料常数S0(t)，m(t)，C(t)均随腐蚀时间变化，但当腐蚀时间为ti(i=1,2,…,n)时，参数S0(ti)，m(ti)，C(ti) 则均为常数。若各应力水平Sj(j=1,2,…,n)仅做一个试件测试，可采用单点-似然法[8]确定式(2)中各参数。令：

(3)

式(2)可表示为：

y=βi,0+βi,1x

(4)

据一元线性回归数学模型[11]，式(4)可表示为：

y=βi,0+βi,1x+ε(S)

(5)

式中：βi,0+βi,1x为y随x线性变化部分；ε(S)为随机误差项，某一特定腐蚀环境下设其为仅依赖于应力水平Sj(j=1,2,…,n)的随机变量，且ε(S)服从标准正态分布，标准差为ε(S)。不难发现，n对测点(xj,yj)，y可视为两部分叠加：x的线性函数βi,0+βi,1x及由应力水平Sj产生的随机因素影响。因此，式(5)可认为xi，yi之间存在关系：

yj=βi,0+βi,1xj+ε(Sj)

(6)

式中：ε(Sj)～N[0，ε2(Sj)]，且各ε(Sj)相互独立。yj～N[βi,0+βi,1x，ε2(Sj)]，通常假定ε(Sj)与lnSj成线性关系[4]，若假定x0=∑(lnSj)/n对应的标准差为σ0(ti)，则σ(Sj)可表示为：

σ(Sj)=σ0(ti)(1+βi,2(lnSj-x0))=σ0(ti)I(Sj,βi,2)

(7)

因此，yj的概率密度函数可表示为：

(8)

据最大似然性原理[10]，对yj的似然性函数取自然对数，并令F=lnL，有：

(9)

由极大似然性原理，分别对F求变量βi,0，βi,1，βi,2，σ0，S0(ti)的偏导，并令其为0，有：

(10)

由式(10)得：

(11)

(12)

(13)

(14)

式中：

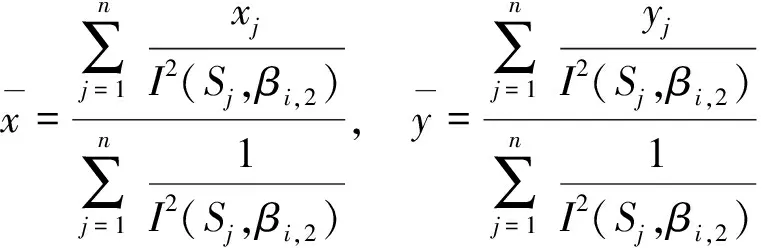
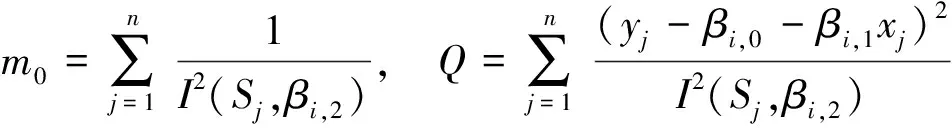
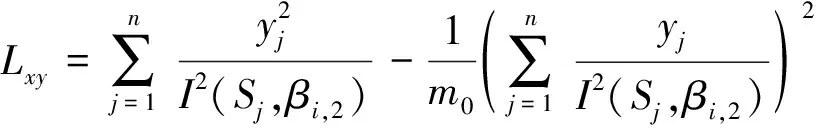
式(11)～式(14)均为S0(ti)，βi,2的二元函数。为精确求得βi,0，βi,1，σ0(ti)值，由相关系数优化法[10]，可使相关系数绝对值|r|最大，即：

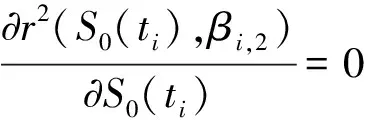
(15)

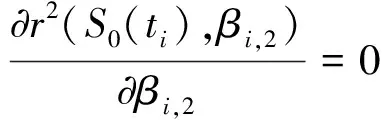
(16)

式中：

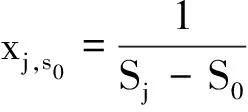
据文献[9]，由式(10)数值解即可获得各系数，但该方法每次迭代求解过程中均需将假定的S0(ti)，βi,2值代入式中计算βi,0，βi,1，σ0(ti)的假定值，再将各系数值代入式(10)进行循环往复数值计算，确定各系数取值。每次假设S0(ti)，βi,2值后，再重新计算βi,0，βi,1，σ0(ti)值，不仅计算量大、计算过程繁琐，在迭代循环计算过程中亦会引入βi,0，βi,1，σ0(ti)的不确定因素。为此，本文基于回归分析方法[7]，将单点-极大似然法与相关系数优化法结合，提出计算步骤为：

(3) 将各系数值代入式(10)、式(14),验证各系数取值的精确性。若式(10)计算值不为0或与0相差较大则调整步骤(1)中S0(ti)，βi,2的取值，再重复上述步骤，但S0(ti)，βi,2的取值需使式(14)绝对值接近1。

1.2 腐蚀疲劳t-P-S-N曲面估计式

用上述计算步骤，据试验数据分别计算出腐蚀时间ti(i=1,2,…,n)系数βi,0，βi,1，βi,2，σ0(ti)，S0(ti)。由各数据随腐蚀时间t的变化规律，获得S0(t)，m(t)，C(t)，σ0(t) 表达式。由于Y～N[β+βx1，σ2(Sj)]，故当可靠度为p时，有：

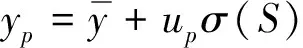
⟺lnNp=lnN+upσ0(t)×

(17)

将式(2)代入式(17)，即可确定任意腐蚀时间t时P-S-N曲线三参数幂函数估计式为：

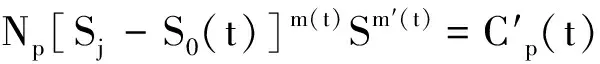
(18)

2 腐蚀疲劳试验

2.1 试验概况

本试验通过MTS电液伺服加载系统对70×5 mm的Q345等边角钢进行腐蚀疲劳试验，加载频率4 Hz,见图1。据角钢构件在输电塔体中的连接构造要求对试件加工开孔，孔直径20 mm；为避免腐蚀削弱试件连接部位材料性能及真实反映试件中部构造部位疲劳性能，试验中对试件端部进行防腐处理，试件最终加工状态见图2。

利用浓硫酸、硝酸、盐酸及蒸馏水按一定比例配置成PH=2的酸性溶液[12]。并用“浸泡-晾置”腐蚀方式对试件进行腐蚀，即将试件在酸性溶液中浸泡2 h，取出后在空气中晾置2 h，如此往复循环3次，共12 h为一次完整腐蚀。腐蚀疲劳试验中采用“腐蚀-疲劳”交替循环加载方式，即将试件腐蚀12 h后再进行疲劳振动。为研究Q345等边角钢疲劳性能随腐蚀时间变化规律，分别对三组试件进行“腐蚀-疲劳”交替循环2次、3次、4次，腐蚀时间t1，t2，t3分别为24 h，36 h，48 h。各组试件等幅疲劳荷载水平相同，共6级。每级荷载水平均采用一个角钢构件进行单点试验。

图1 MTS电液伺服加载系统

2.2 试验现象

试件浸泡于酸性溶液中会缓慢产生大量气泡附着容器壁，浸泡2 h后试件表面及容器底壁均有灰黑色反应产物，见图3(a)。试件浸泡后置于空气中，表面的腐蚀液与氧气接触致腐蚀速率加快，随腐蚀液蒸发腐蚀速度逐渐减慢，因在空气中晾置时间较短，且无风自然蒸发，致试件表面产生一层较厚的红褐色铁锈，见图3(b)。不同腐蚀时间内，同一荷载水平作用下试件疲劳破坏模式见图4。三组试件破坏模式基本相同，断口较整齐，均呈现脆性破坏典型特征。但试验过程中三组试件存在差异，振动荷载较大时试件受腐蚀时间影响不明显，有塑性破坏特征；随振动荷载减小，试件腐蚀时间越长，振动疲劳次数越少，腐蚀致疲劳性能退化越显著。

图3 试件“浸泡-晾置”后状态

2.3 试验结果

2.3.1 不同腐蚀时间内P-S-N曲线估计式建立

各级荷载水平作用下，三组试件经不同“腐蚀-疲劳”循环次数后疲劳寿命见表1。对比分析知，各级荷载水平作用下试件疲劳寿命随腐蚀时间增加而减小；荷载水平较高时，试件疲劳寿命受腐蚀时间影响较小，但随荷载水平降低，腐蚀时间对试件疲劳寿命影响逐渐显著。如，Smax为156.22 MPa时，试件由2次“腐蚀-疲劳”循环增加到3、4次时，腐蚀时间均增加12 h，但疲劳寿命却依次降低18%，10%。据表1，用1.1节系数求解步骤分别确定三组Q345等边角钢构件经不同腐蚀时间后S-N曲线各系数见表2。

表1 不同腐蚀时间疲劳寿命试验结果

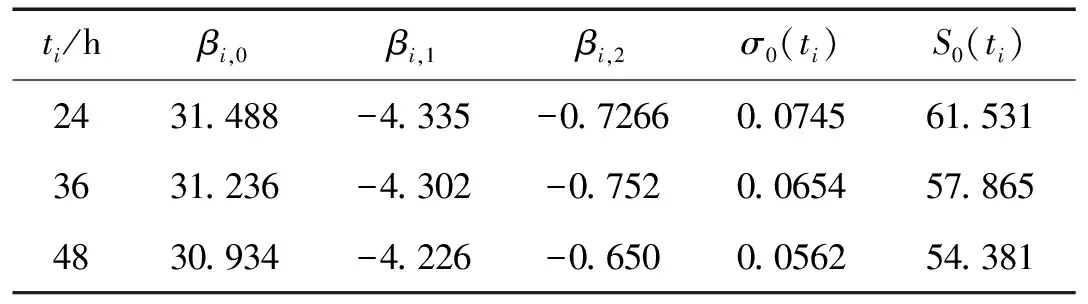
表2 不同腐蚀时间内S-N曲线参数

由统计表[11]查得可靠度为50%、99%时up分别为0，-2.326，将up值与表2参数值代入式(3)、式(18)计算可靠度为50%、99%时不同腐蚀时间对应的P-S-N曲线方程各参数见表3；将表3参数代入式(18)确定三组腐蚀时间对应的P-S-N曲线方程；据表1试验结果及腐蚀时间P-S-N曲线方程绘制试验数据分布与P-S-N曲线变化，见图5，从而可直观形象验证方程参数的精确程度。

表3P=50%，99%时腐蚀疲劳P-S-N曲线参数随时间变化规律

Tab.3Thevariationtrendofmaterialparameterswiththereliabilitylevelsof50%and99%withindifferentcorrosiontime

ti/hm(ti)S0(ti)P=50%P=99%C′0.5(ti)C′0.99(ti)m′(ti)244.33561.5314.732 10132.024 1013-0.126364.30257.8653.677 10131.889 1013-0.100484.22654.3812.719 10131.511 1013-0.085

2.3.2 不同腐蚀时间P-S-N曲面估计式建立

本文的可靠度P为50%、99%时各参数随腐蚀时间变化关系式为：

(19)

(20)

(21)

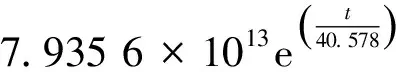
(22)

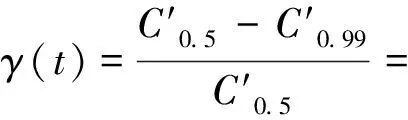
(23)

(24)

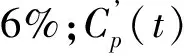
图5 P=50%、99%时不同腐蚀时间P-S-N曲线

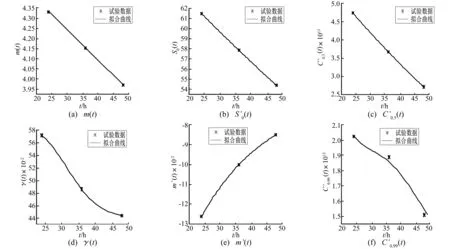
图6 各参数随腐蚀时间变化规律

将式(19)～式(24)代入式(18)，确定P为50%、99%时70×5 mm的Q345等边角钢腐蚀疲劳寿命随腐蚀时间变化曲面方程为：

Np=f(Smax,t)

(25)

式中：若t=0～50 h，Smax=100～500 MPa及P= 99%时疲劳寿命变化曲面见图7。曲面随t，Smax的变化趋势形象反映出角钢构件疲劳寿命变化规律。相同Smax作用下曲面翻卷最大高度随t急剧下降反映出相同Smax作用下试件疲劳振动次数随t增加而显著减少；相同腐蚀时间内疲劳寿命随t的变化规律与图5相似，随Smax值的增加腐蚀时间对疲劳寿命影响逐渐减弱，曲面趋于平坦。

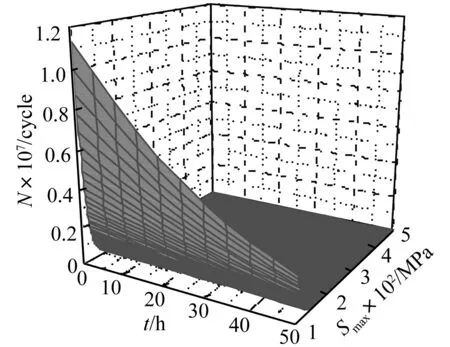
图7 P=99%时不同腐蚀时间S-N曲面

3 结 论

(1) 通过将单点-似然法与相关系数优化法结合，提出确定某腐蚀时间内S-N曲线表达式各参数的改进回归分析方法，并给出实现算法。

(2) 通过回归分析方法结合概率分析建立随腐蚀时间变化的t-P-S-N曲面表达式。通过三组不同腐蚀时间的18根足尺Q345等边角钢试件疲劳试验结果，分析P-S-N曲面方程中各参数随腐蚀时间的变化规律，并给出相应表达式。

(3) 综合各参数随腐蚀时间变化规律，建立反映Q345等边角钢试件t-P-S-N曲面模型。通过该模型计算结果发现，相同疲劳荷载水平作用下试件疲劳寿命随腐蚀时间急剧减小；同一腐蚀时间内疲劳寿命受腐蚀因素影响程度随荷载减小而增加。

参 考 文 献

[1]ASTM E468-76, American society for testing and materials[R]. Philadelphia, 1976.

[2]Nakazawa H, Kodama S S.StatisticalS-Ntesting method with 14 specimens: JSME standard method for determination ofS-Ncurves[C]. In: Statistical research on fatigue and fracture. New York: Elsevier Applied Science, 1987: 59-69.

[3]Nishijima S. Statistical analysis of small sample fatigue data [C]. In: Statistical research on fatigue and fracture. New York: Elsevier Applied Science, 1987:1-19.

[4]Ling J, Pan J. A maximum likelihood method for estimatingP-S-Ncurves[J]. International Journal of Fatigue, 1997, 19(5): 59-69.

[5]傅惠民.a-N(a-t)曲线三参数幂函数拟合法[J]. 航空学报, 1989, 10(12): 666-670.

FU Hui-min. A method of three-parameter power function for fittinga-N(a-t) curve[J]. Acta Aeronautica et Astronautica Sinica, 1989, 10(12): 666-670.

[6]傅惠民.ε-N曲线三参数幂函数公式[J]. 航空学报, 1993,14(3):173-176.

FU Hui-min. A formula of three-parameter power function forε-Ncurves[J]. Acta Aeronautica et Astronautica Sinica, 1993, 14(3): 173-176.

[7]傅惠民. 三参数幂函数回归分析[J]. 航空学报, 1994, 9(2):186-190.

FU Hui-min. Regression analysis of three-parameter power functions [J]. Acta Aeronautica et Astronautica Sinica, 1994, 9(2):186-190.

[8]熊俊江, 黄新宇, 高镇同. 极大似然法对比试验研究及其试验数据处理[J]. 航空学报,1996,17(5):539-542.

XIONG Jun-jiang, HUANG Xin-yu,GAO Zhen-tong. Comparative test study for the maximum likelihood principle and the treatment of its fatigue test data [J]. Acta Aeronautica et Astronautica Sinica,1996,17(5): 539 -542.

[9]熊俊江. 疲劳断裂可靠性工程学[M]. 北京：国防工业出版社, 2008.

[10]高镇同, 熊俊江. 疲劳应用统计学[M]. 北京：国防工业出版社,1986.

[11]张春涛. 腐蚀环境和风振疲劳耦合作用下输电塔线体系疲劳性能研究[D]. 重庆:重庆大学, 2012.

[12]陈晓龙, 施庆生, 邓晓卫. 概率论与数理统计[M]. 南京:东南大学出版社,2011.