基于波函数法的结构振动功率流研究

杨 念， 陈炉云， 张裕芳

(上海交通大学 海洋工程重点实验室，上海 200240)

现代工业愈发展，人对舒适度要求愈高，结构振动噪声愈受关注。结构振动按频段可分为低、中、高三频段。低频段，常用确定性方法如有限元法(FEM)[1-2]分析结构。但随频率增高，有限元法需大幅提高自由度方能获得较准确结果[3]，且仍存在计算发散问题。而高频振动模态密度高，不确定性对响应影响大，常用概率性方法分析：即统计能量法(SEA)[4]、功率流有限元法(EFEM)[5]等。处于高、低频之间的中频段，其模态密度既未达统计能量法对模态重叠因子大于1要求，而结构细节对响应尚有一定影响。因此，在该频段用有限元法、统计能量法效果均不理想。目前主要处理方法采用混合有限元法及统计能量分析法(混合FE-SEA法)[6]，该方法核心为直混场互惠定理。虽混合FE-SEA法对中频问题预测取得一定成果，但理论、计算精度尚存一定问题。Desmet[7]采用基于波理论的新型确定性方法-波函数法(WBM)。该方法基于间接Trefftz法[8]，具有自由度少、收敛快、精度高等优点，在解决中频振动问题时能克服有限元法等确定性方法存在的不足[9-11]。

据WBM理论可快速计算出中频段结构动力响应参数。在结构动力响应中，振动传递主要是能量的传递，由能量角度研究振动响应更能反映问题的本质[12]。通过引入能量流动概念，可得关于结构动力响应功率流分布特性，并可用于结构在中频域的减振降噪评价。功率流作为能同时表征振动水平与振动传递的参数，既包含力、速度幅值大小也包括两者间相位关系，给出的结构振动绝对度量物理量，可清楚描述结构动力响应特性。此外，用波函数法(WBM)求解功率流问题，既能利用方法自身自由度少、收敛快的优势，又能避免求解力、速度等二级参量过程中精度损失问题。因此，WBM法在中频功率流领域潜力巨大。

本文用WBM法对结构功率流进行研究。以求解四周简支平板振动功率流为例，验证该方法的有效性与优势。

1 WBM基本理论

WBM法为间接Trefftz方法，将结构分成少量子域，按Trefftz准则，每个子域的振动参量由一组波函数表示，该波函数严格满足振动控制方程，因此整个控制域内的参量足够精确，只在边界上产生误差。边界误差通过加辽金加权残值法计算消除[9]，求出位移场。

1.1 薄板弯曲振动理论

本文主要研究板的弯曲振动问题。该问题的理论主要有Kirchhoff[13]及Reissner-Mindlin[14-15]平板理论。对薄板(弯曲波波长不小于板厚的6倍)，Kirchhoff 理论计算结果较准确[16]。而WBM法基于该理论。据Kirchhoff 理论，均匀各向同性平板受法向作用力时，决定其稳态法向位移场方程为：

(1)

式中：w(x,y)为法向位移场；为作用力；(xF,yF)为作用力坐标；为板抗弯刚度；为板弯曲波数；t,E,μ,η,ω,ρ分别为板厚、弹性模量、泊松比、材料损失系数、激振圆频率及材料密度；

由于Kirchhoff 理论中的控制方程为四阶微分方程，因此须在板边界添加两边界条件以确定弯曲振动位移场w(x,y)。边界条件主要有3种：

(1)力边界条件ΓmQ(已知弯矩、剪力，如自由边界)：

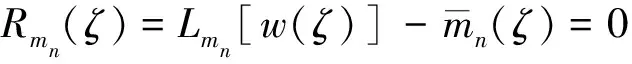
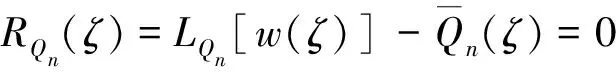
(2)位移边界条件Γwθ(已知线位移、转角，如固支边界)：

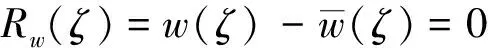
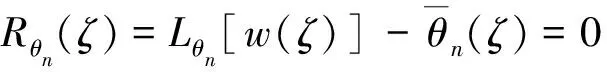
(3)混合边界条件Γwm(已知线位移、弯矩，如简支边界)：

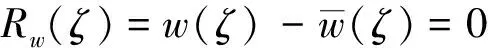
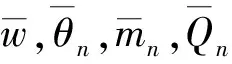
1.2 位移参量w展开

在WBM中弯曲振动稳态位移场w展开形式[11,15]为：

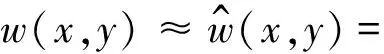
(2)

(3)

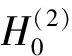
WBM中的波函数ψs(x,y)均为满足控制方程(1)的齐次解，其两组形式[9]为：

第一组：

(4)

第二组：

(5)

其中：

式中，s1=0,1,2,…,ns1;s2=0,1,2,…,ns2；ns=4(ns1+1)+4(ns2+1)为波模型自由度。

现已证明，用第一组波函数求解任意凸域问题时，计算均能收敛。第二组波函数收敛性尚未得到证明，且在求解某些特殊凸域问题时收敛较慢[7]。本文采用第一组波函数求解。理论上只有在取无限个波函数时，计算结果才为精确解，但实际计算中只能取有限个波函数。因此，须对波函数个数进行截断，截断法则[10]为：

(6)

式中：T为截断系数；Lx，Ly分别为包围板轮廓的最小矩形尺寸。

1.3 加辽金加权残值公式

WBM法在边界上会产生误差，可用加辽金加权残值公式消除[7]：

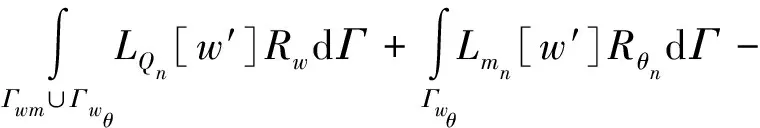
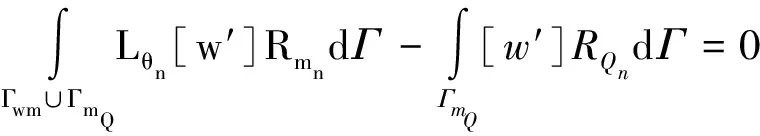
(7)

[A]{ws}={f}

(8)

式中：

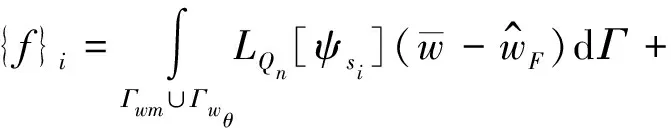
(10)

求解式(7)可得贡献系数ws，从而求出位移场w。

2 WBM计算功率流

2.1 功率流基本理论

记F(ω)为作用于结构某点的外力瞬时值；V(ω)为该点速度响应瞬时值，则输入该结构功率瞬时值[17]为：

P=F(ω)V(ω)

(11)

用复数形式表示为：

(12)

式中：*为取共轭复数。

功率流过某板截面时，可将其视为能量强度，反映该截面振动程度的强弱。研究实际振动结构时，往往取一段时间(周期振动的最小正周期)内的平均功率，其较瞬时功率更能反映外部激励注入结构的能量强度。该时均功率即为稳态功率流强度[18]：

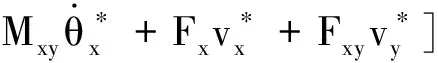
(13)

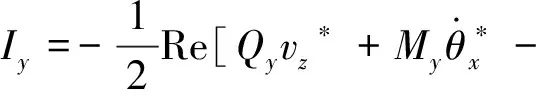
(14)

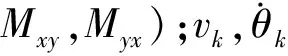
基于Kirchhoff理论，式(13)、(14)可化简为：

(15)

(16)

式中：Qx,Qy,Mx,My,Mxy可通过对位移函数求偏导获得[2]。将其代入式(15)、(16)，可得平板振动功率流。

2.2 功率流计算

由式(15)、(16)可知，计算功率流需已知剪力、弯矩等数值，将1.3节中所得位移场代入计算式中得：

(17)

(18)

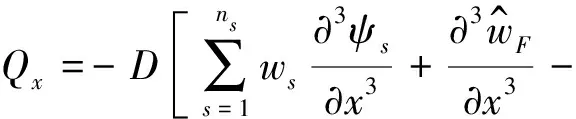
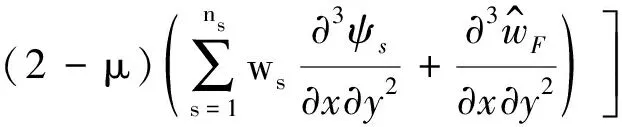
(19)

(20)

将以上数值代入式(15)、(16)即得板的振动功率流。由以上推导看出，功率流仅与贡献系数ws有关，不存在有限元法中求解力、速度等二级参量时精度损失问题。因此，运用WBM法求解功率流理论上是解析解，无精度损失。

3 算例

本文以矩形简支平板为例，用WBM法求解其功率流场，并与有限元法结果对比，验证WBM法的有效性、优势。矩形板见图1，板长Lx=1.0 m，宽Ly=0.5 m，弹性模量E=210 GN，泊松比μ=0.3,密度ρ=7 800 kg/m3，板厚t=0.001 m。为简化，算例中取耗损系数η=0。将单位法向力作用于点rF(xF,yF)=(0.2 m,0.1 m)处。

图1 简支矩形板

3.1 WBM功率流计算

受简谐集中力作用的简支矩形平板，其法向位移场有解析解。本文以通过该解析解求出的功率流场为计算参考值。在集中力F作用下矩形板位移场解析解[19]为：

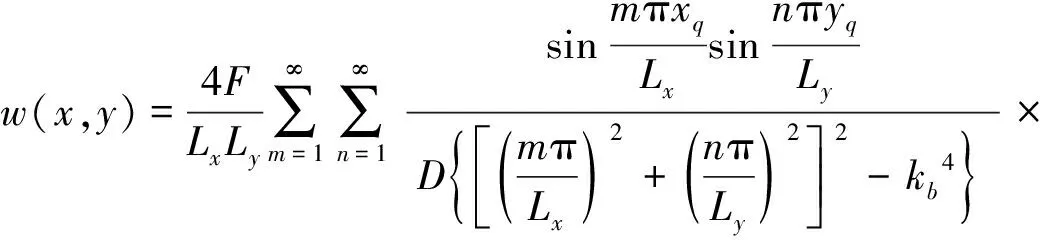
(21)

激振力频率为60 Hz，WBM计算软件用MatlabR2011b，波函数个数为180，即自由度DOF=180。图2(a)为用WBM计算所得位移场等高线图，该位移场与解析解间相对误差见图2(b)，相对误差ε1=|(w-w0)/w0|中w0为理论值。可以看出，除边界附近与位移值近于0区域外，板上大部分响应点位移与理论值接近，相对误差不超1%。

对所求位移场进行相关后处理，得板在该激振频率下功率流场等高线图见图3(a)， 与解析解相对误差见图3(b)，相对误差ε=|(P-P0)/P0|中P0为理论值。可以看出，除边界附近及位移值近于0区域外，板上大部分响应点功率流与理论值接近，相对误差不超过5%。

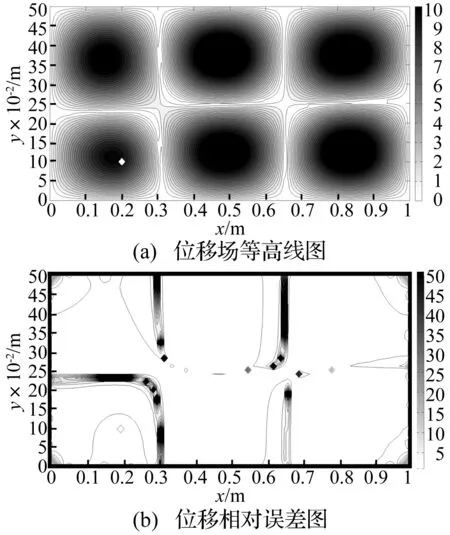
图2 位移场等高线及相对误差图

图3 功率流等高线及相对误差图

3.2 与有限元法(FEM)对比

选100～500 Hz为分析频段，分别用WBM法及有限元法求解响应点rr(xr,yr)=(0.6 m,0.4 m)处功率流。WBM法计算软件用Matlab R2011b， DOF=180；有限元软件选Nastran2010，自由度数DOF=24 855。将两种方法所得结果分别与理论值比较，计算得功率流谱见图4。由图4看出，低频时，WBM法及有限元法所得结果与理论值较吻合。随频率增高，有限元法与理论值误差增大；用WBM法所求功率流与理论值较吻合，计算精确性仍可得到保证，求解频段可由低频一直扩展至中频，表明WBM法对解决中频功率流问题具有优势。

4 结 论

本文通过对板结构振动的研究， 使WBM法获得有效性验证；通过与有限元法比较，体现出WBM法在求解中频振动功率流时自由度少、收敛快、精度高等优势。后续会采用更复杂模型进行分析与控制研究，力求将该方法用于实际结构振动分析中。

参 考 文 献

[1]Gavric L, Pavic G. A finite element method for computation of structural intensity by the normal mode approach[J].Journal of Sound and Vibration,1993,164(1):29-43.

[2]Hambric S. Power flow and mechanical intensity calculations in structural finite element analysis[J].Journal of Vibration and Acoustics,1990,112(4):542-549.

[3]Cabos C, Jokat J. Computation of structure-borne noise propagation in ship structures using noise-FEM[C]//Proce-eding of the Seventh International Symposium on Practical Design of Ships and Mobile Units, Netherlands, New York:Hague Elsevier,1998:927-934.

[4]Lyon R, DeJong R. Theory and application of statistical energy analysis (2nd ed)[M]. Butterworth:Heinemann,1995.

[5]Woblever J C. Vibrational power flow analysis of rods and beams[D].Lafayette,Indiana:Mechanical Engineering Depa-rtment,Purdue University,1988.

[6]陈书明，王登峰，宋学伟,等.基于FE-SEA混合方法的声腔内部噪声预测[J].振动与冲击,2010,29(10):236-238.

CHEN Shu-ming, WANG Deng-feng, SONG Xue-wei, et al.Interior noise prediction of a sound cavity based on hybrid FE-SEA method[J]. Journal of Vibration and Shock, 2010, 29(10):236-238.

[7]Desmet W. A wave based prediction technique for couple-dvibro-acoustic analysis[D]. Leuven:Katholieke Universite-it Leuven, Departement Werktuigkunde,1998.

[8]Trefftz E.Eingegenstuck zum ritzschen verfahren[C]//Proce-edings of the Second International Congress on Applied Mechanics,Zurich,Switserland,1926:131-137.

[9]Vanmaele C. Development of a wave based prediction technique for the efficient analysis of low and mid-frequencystructural vibrations[D]. Leuven:Katholieke Universiteit Leuven, Departement Werktuigkunde, 2007.

[10]Vanmaele C, Vandepitte D, Desmet W. An efficient wav-e based prediction technique for plate bending vibrations[J]. Computer Methods in Applied Mechanics and Engineering,2007,196(33-34):3178-3189.

[11]何雪松，黄其柏，胡 溧.WBM法在薄板弯曲振动分析中的应用[J].华中科技大学学报(自然科学版),2008,36(7):97-99.

HE Xue-song, HUANG Qi-bai, HU Li.Application of wave based method to plate bending vibration analysis[J]. Huangzhong Univ. of Sci. &Tech. (Natural Science Edition), 2008, 36(7):97-99.

[12]严济宽，柴 敏，陈小琳.振动隔离效果的评定[J].噪声与振动控制,1997,6:22-30.

YAN Ji-kuan, CHAI Min, CHEN Xiao-lin.The evaluateion of vibration isolation performance[J]. Noise and Vibration Control,1997,6:22-30.

[13]Leissa A.Vibration of plates[M]. Woodbury:Acoustical Society of America,1993.

[14]Mindlin R.Influence of rotary inertia and shear on flexural motions of isotropicelastic plates[J].Journalof Applied Mechanics ASME, 1951, 18:31-38.

[15]Reissner E.The effect of transverse shear deformation on the bending of elastic plates[J].Journal of Applied Mechanics ASME, 1969,3(3):534-547.

[16]Cremer L, Heckl M, Ungar E.Structure-borne sound:structural vibrations and sound radiation ataudio frequencies[M].Verlag: Springer, 1973.

[17]杨德庆，罗 放，陈 静.有限元功率流落差计算方法研究[J]. 噪声与振动控制,2009,6:127-131.

YANG De-qing, LUO Fang, CHEN Jing. Power flow level difference finite element analysis[J]. Noise and Vibration Control,2009, 6:127-131.

[18]Junger M, Feit D. Sound, structures, and their interactions[M]. Woodbury: AcousticalSociety of America,1993.

[19]曹国雄. 弹性矩形薄板振动[M]. 北京:中国建筑工业出版社,1983.