密闭空间内爆炸缩比相似模型研究

杨亚东， 李向东， 王晓鸣， 张刘成， 张马莉

(1.南京理工大学 智能弹药技术国防重点学科实验室，南京 210094；2中国工程物理研究院 化工材料研究所，四川 绵阳 621900；3.北方华安工业集团有限公司，黑龙江 齐齐哈尔 161046)

发生在有限定边界条件的密闭或半密闭结构内部的爆炸称内爆炸。与自由场爆炸不同，内爆炸产生的高温、高压产物无法及时向外扩散，冲击波在结构壁面来回反射，反射波之间相互叠加作用使超压峰值增大，作用时间加长，对结构内人员、设备等毁伤更大。精确制导武器攻击地下掩体及弹药库、反舰导弹攻击舰船、公共场所发生恐怖袭击等均可归为内爆炸。近年来探索内爆炸对结构冲击作用机理、对内爆炸进行危害评估、预测结构破坏程度已成研究热点。Baker等[1]所提内爆炸荷载简化模型认为反射波逐次减弱，且以前三个脉冲为主，为目前常用模型；Beshara[2]通过对地表建筑结构发生内部爆炸现象研究，认为结构内爆炸荷载由动态压力及爆轰产物膨胀产生的准静态压力所组成；Remennikov[3]采用多种数值仿真方法预测密闭结构内恐怖袭击的破坏效应；Lu等[4]对发生在混凝土结构弹药库内的爆炸现象进行研究，用理论与实验相结合方法提出有开口的混凝土结构内爆炸时碎片飞散速度预测公式；杨科之等[5]用等效单自由度法推导出内爆荷载作用下结构等效静载的动效系数解析式的简化表达式，便于结构抗内爆炸设计。郭志昆等[6]进行扁平箱形密闭结构内爆炸试验研究，发现作用于结构内表面的压力呈非线性下降，且压力时程曲线主要由一个初始主脉冲与几个较大后续脉冲组成。

受试验技术、科研经费及试验周期等条件制约，对大型建筑结构进行原尺寸内爆炸试验难度较大，而用缩比模拟技术[7]可实现之。为使缩小后内爆炸试验能真实反映全尺寸内爆炸试验的毁伤特性，确定完整的内爆炸毁伤特性影响因素，需建立正确的缩比试验相似准则。目前对密闭结构内爆炸现象是否满足相似规律、密闭结构内爆炸缩比模型试验是否受尺寸效应影响等研究较少，尚需相关研究验证。

本文运用量纲理论导出典型建筑结构内爆炸的相似规律，建立密闭空间内爆炸相似理论模型。在理论分析基础上对原模型进行药量递增直至结构破坏的仿真计算，研究药量变化对结构毁伤影响，并以原模型结构产生裂纹的临界装药量为依据进行缩比模型计算，研究缩比模型壁面典型位置处冲击波反射超压变化规律，揭示缩比系数对内爆炸毁伤参量影响，验证缩比模型毁伤形态是否相同，为内爆炸相关研究提供参考。

1 密闭空间内爆炸相似模型

1.1 密闭空间内爆炸毁伤参数影响因素

爆炸冲击波对结构的破坏作用主要由两特征量度量：① 作用于结构壁面的冲击波超压Δp；② 冲击波冲量i。两特征量的影响因素有：

(1) 炸药参数：炸药质量Q；炸药密度ρe；单位质量炸药释放的化学能e；爆炸产物膨胀指数γe。

(2) 空气参数：初始状态压力p0；空气密度ρa；空气绝热指数γa。忽略如空气粘性、传热性及空气温度等次要因素。

(3) 结构参数：长l，宽b，高h；强度σ；杨氏模量E；材料密度ρs。

(4) 壁面与爆心距离R。

1.2 密闭空间内爆炸量纲分析

以长度、质量、时间量纲M，L，T为基本量纲，各物理量量纲见表1。

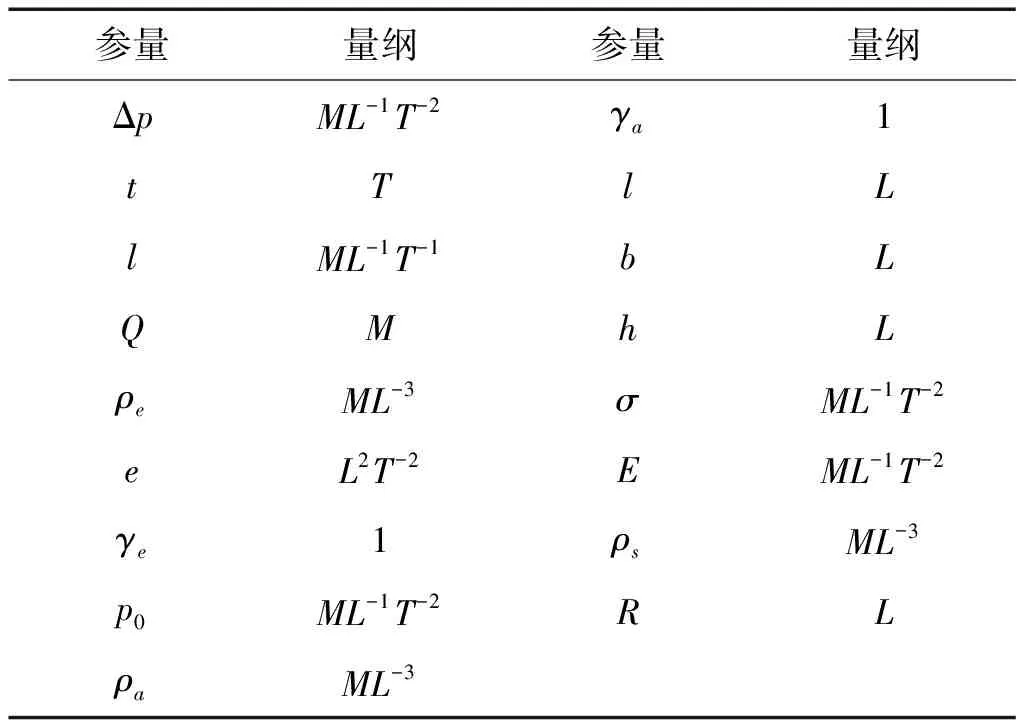
表1 内爆炸相关参量及其量纲

据相似第二定律(∏定理)，内爆炸壁面冲击波超压与影响因素的函数关系为：

Δp=f(Q,ρe,e,γe,p0,ρa,γa,l,b,h,σ,E,ρs,R)

(1)

对缩比模型而言，若结构材料与原型相同，则杨氏模量E不是独立量可略去；γe，γa为无量纲量，符合相似定律无量纲原则，亦可省略。故式(1)简化为：

Δp=f(Q,ρe,e,p0,ρa,l,b,h,σ,ρs,R)

(2)

以Q，ρe，e为基本量，式(2)可写成无量纲形式：

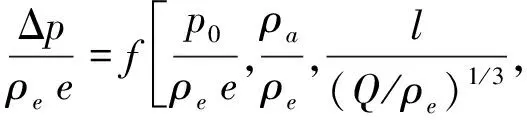
(3)

同理，仍以Q，ρe，e为基本量，由量纲分析可得装药在密闭空间内爆炸时，作用于结构壁面的冲量i满足的相似规律为：

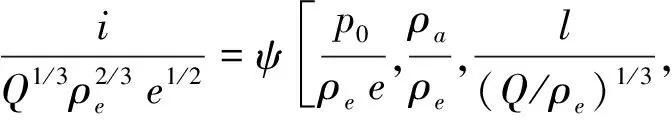
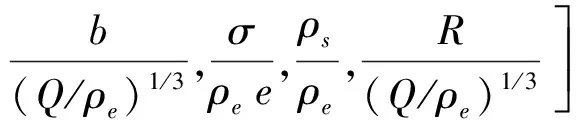
(4)

2 计算模型及材料参数

2.1 有限元模型及算法

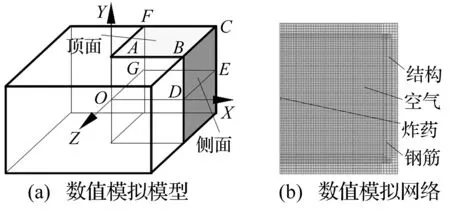
图1 数值模拟模型及网格

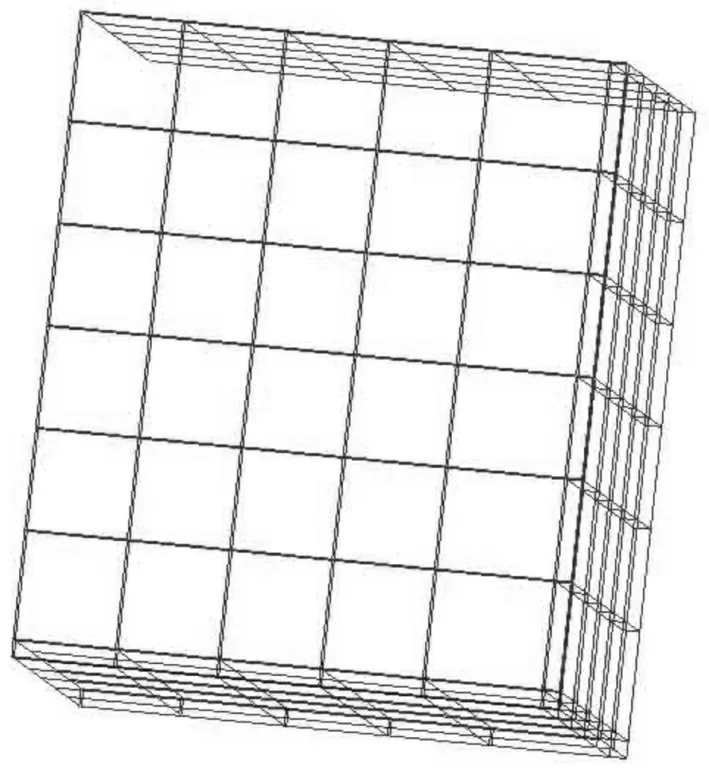
图2 钢筋框架结构

有限元模型见图1(a)，密闭结构为长600 cm×宽600 cm×高350 cm的钢筋混凝土建筑，底板、侧墙厚30 cm，顶板厚18 cm，墙体配筋率0.5%，用C30混凝土浇筑钢筋框架，见图2。钢筋型号HRB335，直径22 mm，在底板、侧墙厚度方向布两层，顶板厚度方向布一层。装药位于密闭空间中心，装药用TNT炸药。考虑结构对称性，取1/4模型建模分析。结构用单点积分Lagrange六面体网格，炸药、空气用Euler六面体网格。钢筋以梁单元形式嵌于混凝土中，两种单元以共节点进行藕合，用流-固耦合方法求解Lagrange单元与Euler单元之间的相互作用。

2.2 材料模型及参数

TNT炸药采用High_Explosive_Burn材料模型与JWL状态方程描述，状态方程为：

(5)

式中：V为相对体积；E为初始内能；A，B，R1,R2，ω为常数。TNT参数见表2。

表2 TNT参数

用Plastic_Kinematic模型模拟钢筋在冲击载荷作用下受力情况。钢筋参数：密度ρ=7.85×103kg/m3；弹性模量E=2.1 GPa；泊松比ν=0.22；屈服强度σs=335 MPa；失效塑性应变εp=0.8。混凝土采用的HJC模型[8-9]考虑动载下混凝土本构特征，可模拟混凝土材料破碎及崩落现象，参数为：最大抗压强度fc=48 MPa；弹性模量Ec=20.68 GPa；泊松比ν=0.2；密度ρ=2.44 g/cm3；抗拉强度ft=4 MPa。

3 密闭空间内爆炸相似规律数值模拟

利用LS-DYNA对原模型进行药量逐次增加直至结构破坏的仿真计算，研究结构尺寸不变而药量变化时内爆炸现象是否具有相似规律，并以原模型结构产生裂纹的临界装药量为依据进行缩比模型计算，验证临界药量在缩比模型中是否服从相似的毁伤形态，为能否以缩比模型试验验证原模型试验提供理论依据。

3.1 结构毁伤分级及易损面分布特性

图3为不同质量装药对钢筋混凝土结构毁伤情况，Pi为壁面入射超压。计算表明，装药质量小于1.1 kg时结构不发生破坏；大于1.1 kg时，结构较薄弱的顶板角点出现裂纹，直至装药小于1.4 kg区域顶板主要以剪切破坏裂纹为主，且无通透裂纹出现，该段区域定义为裂纹区；装药质量大于1.4 kg时，顶板与侧墙交接处、顶板角点出现剪切通透破坏裂纹，顶板正中出现冲切破坏裂纹[10]，此区域定义为破损区。在破损区内，前期小装药量只会使内部钢筋产生变形而不会断裂。装药量继续增大时，顶板内部位于侧墙交接处的钢筋在墙体剪切作用超过钢筋抗剪强度时出现剪切断裂。

由于结构底面为正方形，且装药位于结构几何中心，由图1(a)知，每个面以爆心投影点为中心呈对称分布特性，结构四个侧面分布特性应相同，顶板较薄为易损壁面，取顶板及侧壁冲击波超压与冲量进行对比，找出结构较大受力位置作为测试点，分析结构的冲击波分布特性。

图3 不同质量装药条件下结构毁伤情况

图4为1.1 kg装药作用下顶板、侧面冲击波超压及冲量分布。由图4(a)看出，顶板正对爆心的A点处冲击波超压最大为0.656 MPa，原因为A点离爆心最近；随与A点距离的增加，压力峰值逐渐减小，但在边界BC，FC处压力峰值明显增大，为0.468 MPa，原因为BC，FC为顶板与侧面的交线，在BC，FC处，顶板及侧面的反射冲击波汇聚叠加，造成边界线冲击波超压增大；而两相邻侧面与顶板共同交点C点处冲击波超压增加较明显，其超压值达到0.572 MPa，虽C点为顶板离爆心最远点，但该处受三个面的反射冲击波相互汇聚叠加作用，导致压力增大明显。由此可知，壁面的冲击波超压随测试点与爆心间距离增加而减小，在边界附近因受边界面影响而加强；在C点附近区域内，与BC，FC成45°夹角线冲击波超压较明显，由于两侧面反射冲击波在45°夹角线上汇聚作用最强。因此，当顶板角点在剪力、弯矩作用下超过钢筋混凝土抗拉强度时，顶板会以角点为起点，产生与两边线成45°方向向内生长的弯剪裂纹[10]。图4(b)为顶板超压冲量分布图。顶板的冲量仍为离爆心最近的A点处最大，为3.496 MPa.ms，其次为边界线C点、B点，分别为3.388 MPa·ms，2.708 MPa.ms。侧面的冲击波超压与冲量分布见图4(c)、(d)。由于侧面与爆心距离大于顶板与爆心距离，故侧面中心D点的冲击波超压低于顶板中心A点的冲击波超压，其超压峰值为0.333 MPa。侧面边界BC，FC线的冲击波叠加作用较顶面更明显，使侧面边界中点B、E，三面交点C处冲击波超压大于侧面中心D点处冲击波超压。C点超压峰值最大为0.572 MPa。由此推断，壁面的冲击波超压由测点与爆心距离及测点与相邻壁面的距离共同起作用。壁面离爆心较近时，爆心距离起主导作用；壁面离爆心较远时，与相邻壁面的距离起主导作用。由图4(d)看出，侧面中心E点处冲量最大为4.981 MPa.ms。超压最大的C点冲量反而小于E点，原因为冲量由超压与作用时间共同决定。由顶板、侧面分析结果看出，壁面出现较大冲击波超压及冲量位置分别为：顶板正对爆心的A点、顶板与侧面的交线中心B点(或F点)、两侧面与底面的交点C点、侧面正对爆心的D点、侧面与侧面的交线中心E点，这些点均为结构易损点。

图4 顶板和侧墙上的超压与冲量分布

图5为文献[6]中实验所得墙体破坏形态，由实验获得结构主要破坏形式为：顶板爆心投影点处向外鼓胀，按塑性铰线形破坏；结构顶板角点沿45°线向内开裂；两墙交线中点处出现通长裂缝。该破坏现象与本文计算的破坏形式较相似。

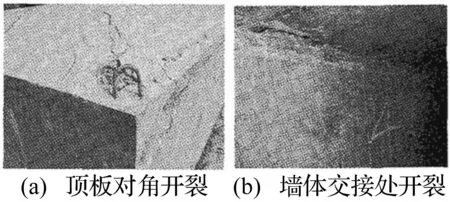
图5 墙体局部破坏情况

3.2 装药质量变化相似性分析

以图4中顶板及侧壁受力较大的A、B、C、D、E点作为典型测量点，研究药量变化、结构尺寸不变时内爆炸现象能否满足相似规律。

由图6看出，药量变化时反射超压总体上不服从相似规律，但仅受单面墙影响的A点、D点及受两面墙影响B点、E点与受三面墙影响的C点分开考虑时却服从相似规律较好(图1(a))。将文献[11]中受单面墙影响的第1、2、4测点试验数据与文献[6]中受双面墙影响的第P2、P4、P5测点试验数据按比例距离换算后与本文计算结果对比看出,文献数据与计算结果吻合较好，说明本文计算结果较合理。在双对数坐标中，反射超压与比例距离呈线性关系。受单面墙影响的A、D点拟合公式为：

ΔP1=1.422r-1.449

(6)

受双面墙影响的B、E点拟合公式为：

ΔP2=3.531r-1.616

(7)

受三面墙影响的C点拟合公式为：

ΔP3=20.072r-2.374

(8)

式中：ΔPi为反射超压(MPa)；i为受影响墙面数；r为比例距离(m/kg1/3)。

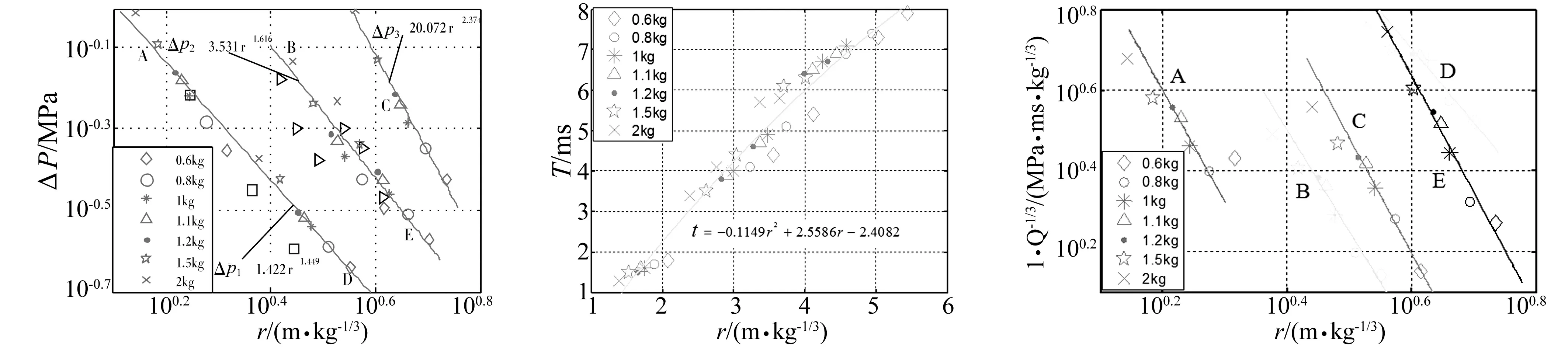
图6 典型位置反射超压与比例距离关系

由图7可见，药量变化时测点冲击波到达时间总体上服从相似规律，其拟合公式为：

t=-0.114 9r2+2.558 6r-2.408 2

(9)

由图8看出，装药量不超过使结构破损的质量时(图3)，各测点比例比冲量按各自位置服从相似规律，在双对数坐标中比例比冲量与比例距离呈线性关系；装药量大于使结构破损的质量时，比例比冲量值低于拟合曲线，不服从相似规律，主要因结构破损导致内部压力减小，作用时间减短。反射超压及冲击波不受结构破损影响主要因结构破损时间落后于该两特征量的提取时间。

3.3 缩比模型相似性验证

以原模型结构产生裂纹的临界装药量为依据进行缩比系数分别为0.8、0.6、0.4、0.2、0.1的缩比模型计算，以此验证临界装药量在缩比模型中是否服从相似规律。

图9为不同缩比模型典型位置反射压力时程曲线。由图9看出，原型与缩比模型各测点压力变化曲线变化趋势较一致，各脉冲峰值变化不大；随缩比系数的减小，缩比模型脉冲宽度逐渐减小。据图9所得典型位置冲击波超压、脉冲宽度及比冲量见表4。

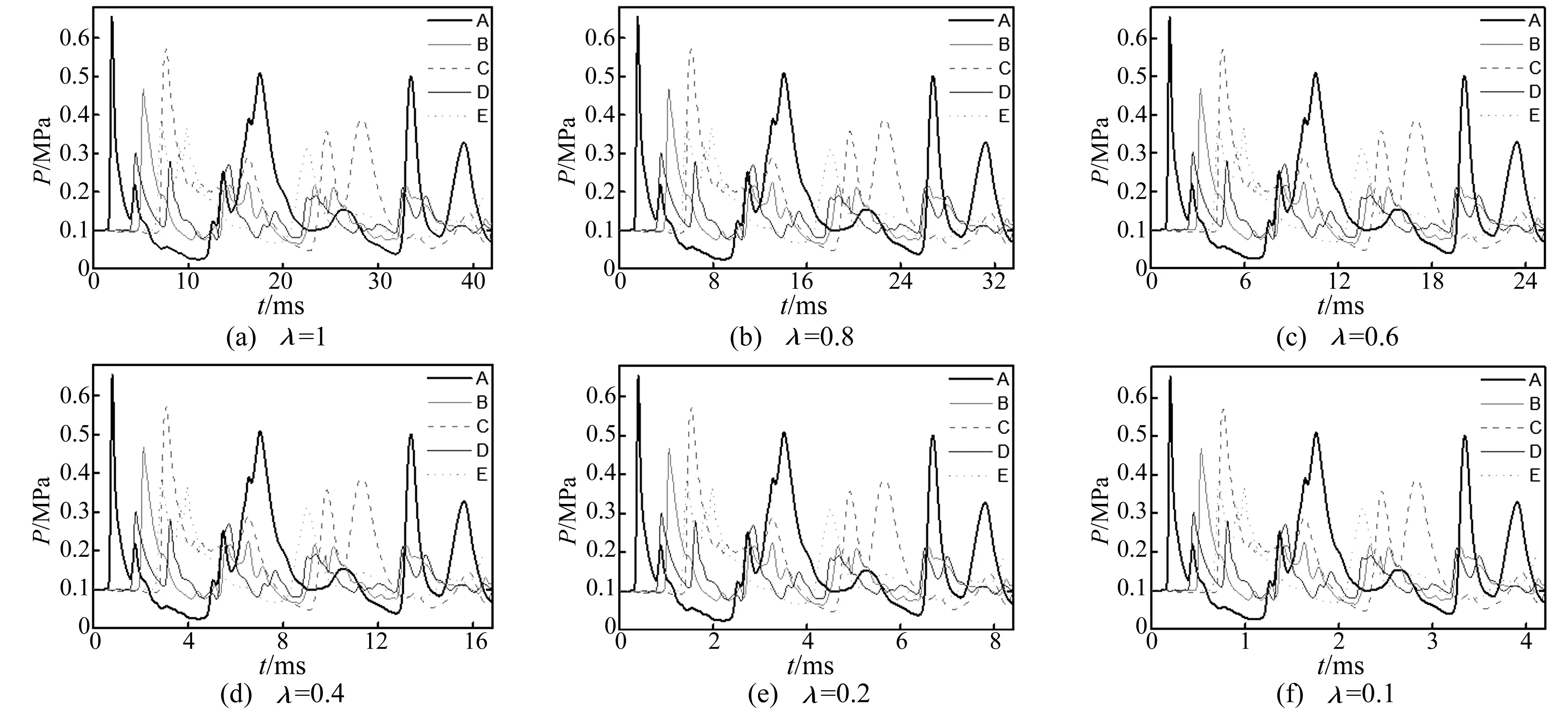
图9 不同缩比模型典型位置反射压力时程曲线

表4 测点冲击波超压、脉冲宽度及比冲量

图10为缩比系数与冲击波超压、脉冲宽度及冲量关系图。由图10看出，随缩比系数的减小，各缩比模型冲击波超压、比例脉冲宽度T/Q-1/3及比例冲量i/Q-1/3与原模型值偏离程度逐渐增大，最大相对误差分别为3.3%、4.96%、5.1%。比例脉冲宽度T/Q-1/3及比例冲量i/Q-1/3偏离程度大于冲击波超压偏离程度。主要原因可能为：① 随缩比系数的减小，脉冲宽度、冲量的取值误差逐渐增大，不及超压峰值计数精确；② 随模型的逐渐减小，边界效应对系统影响逐渐增大。

图10 缩比系数对冲击波超压、比例脉冲宽度、比例冲量影响

图11为缩比模型与原型的顶板裂纹形态，由于计算缩比模型较多，仅给出两种缩比模型与原模型的对比，其余缩比模型裂纹形态相似。由图11看出，结构产生裂纹的时间与裂纹形态均服从相似规律，缩比系数不小于0.1时，各缩比模型与原模型毁伤形态相似。

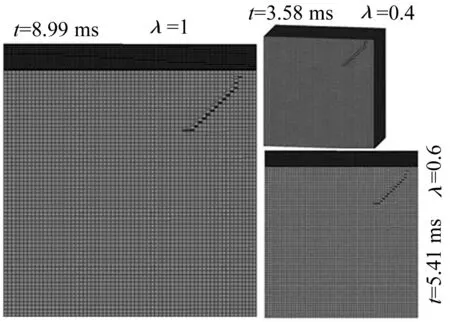
图11 顶板裂纹形态

4 结 论

通过对原模型装药量递增直至结构破坏与以原模型结构产生裂纹的临界装药量为依据的缩比模型内爆炸仿真计算，结论如下：

(1) 结构尺寸不变、药量变化时冲击波服从相似规律；典型位置反射超压以受单、双、三面墙影响分开考虑时服从相似规律；结构不破损时冲量按各自位置分开考虑时服从相似规律；结构发生破损时，冲量不服从相似规律。

(2) 以原模型结构产生裂纹的临界装药量为依据进行缩比模型计算时，缩比模型与原模型壁面的冲击波超压、比例脉冲宽度及比例冲量服从相似规律。计算结果与理论推导吻合性较好，各缩比模型与原模型毁伤形态相似。工程上可采用缩比系数不小于0.1的缩比模型试验结果预测原结构尺寸模型内爆炸毁伤效应。

(3) 随缩比系数的减小，各缩比模型冲击波超压、比例脉冲宽度及比例冲量与原模型值的偏离程度逐渐增大，相似程度呈下降趋势。

参 考 文 献

[1]Baker W E,Cox P A. Explosion hazards and evaluation[M].New York: Elsevier Publishing Company, 1983.

[2]Beshara F B A. Modeling of blast loading on aboveground structures Ⅱ. internal blast and ground shock[J]. Computers and Structures, 1994, 5(51):597-606.

[3]Remennikov A M. A review of methods for predicting bomb blast effects on buildings[J]. Journal of Battlefield Technology, 2003,6(3):5-10.

[4]Lu Y, Xu K. Prediction of debris launch velocity of vented concrete structures unde rinternal blast[J]. International Journal of Impact Engineering, 2007,34(11):1753-1767.

[5]杨科之, 杨秀敏, 王年桥.内爆荷载作用下结构等效静载计算方法[J].解放军理工大学学报,2002,3(4): 31-33.

YANG Ke-zhi, YANG Xiu-min, WANG Nian-qiao. Equivalent static load calculation method of structure subjected to internal explosion[J]. Journal of PLA University of Science and Technology, 2002,3(4): 31-33.

[6]郭志昆,宋锋良,刘 峰,等.扁平箱形密闭结构内爆炸的模型试验[J].解放军理工大学学报,2008,9(4): 345-350.

GOU Zhi-kun, SONG Feng-liang, LIU Feng, et al. Experiment of closed flat box structure subjected to internal detonation[J]. Journal of PLA University of Science and Technology, 2008,9(4): 345-350.

[7]武海军,黄风雷,陈 利,等.动能弹侵彻钢筋混凝土相似性分析[J].兵工学报,2007,28(3): 276-280.

WU Hai-jun, HUANG Feng-lei,CHEN Li,et al. Similarity law analyses of penetration behavior in reinforced concrete [J].Acta Armamentar,2007,28(3): 276-280.

[8]张凤国,李恩征.大应变、高应变率及高压强条件下混凝土的计算模型[J].爆炸与冲击,2002,22(3): 198-202.

ZHANG Feng-guo, LI En-zheng. A computational model for concrete subjected to large strains,high strain rates,and high pressures[J].Explosion and Shock Waves, 2002,22(3): 198-202.

[9]张 舵,卢芳云.混凝土板模爆方法数值模拟研究[J].国防科技大学学报,2007,29(2): 34-38.

ZHANG Duo, LU Fang-yun. A numerical study of scaling modeling method of concrete slab subjected to blast loading[J]. Journal of National University of Defense Technology,2007,29(2): 34-38.

[10]杨 芸.钢筋混凝土平板结构冲切破坏与剪切破坏的研究[D].淮南:安徽理工大学,2009.

[11]陈 昊,陶 钢.温压弹在有限空间内爆炸的超压测试和分析[J].爆破器材,2009,38(5):4-7.

CHEN Hao, TAO Gang. The test and analysis on overpressure generated by thermo-baric grenade explosion in limited space[J].Explosive Materials,2009,38(5):4-7.