考虑外部阻抗的压电叠层作动器机电耦合模型

郑继周，张 艳，贺国华，侯加林

(1.山东农业大学 机电学院,山东 泰安 271018；2.山东省园艺机械与装备重点实验室,山东 泰安 271018；3.山东农业大学 信息学院,山东 泰安 271018)

作为一种智能材料,压电陶瓷已应用于很多场合,如微定位、精密加工、结构故障诊断、振动主动控制等。这主要归功于其良好的动力学特性及其它特点,如结构紧凑、易于集成、无需维护以及较长的使用寿命等。

由于压电效应,压电片与主体结构结合后,二者之间呈现出明显的机电耦合特性。针对这种特性,已有很多学者进行研究,并提出了很多数学模型,主要有静态等效力模型[1]、有限元模型[2]和阻抗模型[3～5]等。与静态法或者有限元法相比,基于阻抗的建模方法更适合于机电耦合系统建模,更能反映系统的物理本质。这是因为,对于压电驱动结构,作动器产生的力依赖于压电元件和主体结构的阻抗特性。

压电叠层作动器具有出力大、响应快、低电压、作动能力强等优点,适合于柔性结构振动控制。Flint等[6]应用阻抗法和转换方程法研究了压电叠层作动器的动力学特性。通过假设作动器外壳的阻抗远大于压电片和预紧弹簧的阻抗,从而得到固定-自由边界条件。李俊宝等[7]利用力学等效原理建立了压电主动构件的动力学模型。郑凯等[8]实验研究了预紧力对压电叠层作动器性能的影响。Wang 等[9]设计了一种π型压电叠层作动器,并应用热-弹类比理论对振动主动控制系统进行建模。靳宏等[10]用阻抗测试法分析了压电叠层作动器的动态特性。

受文献[6]的启发,本文考虑了更具一般性的情况。在工程实际应用中,压电叠层作动器往往用于梁、板以及桁架等柔性结构中。在这种情况下,作动器两端的外部阻抗均为有限值。因此,采用两端自由的杆来模拟压电叠层作动器更符合实际情况。以压电材料的本构关系和一维杆模型为基础,推导了短路机械阻抗矩阵(包括原点阻抗和跨点阻抗)、电导纳以及压电叠层作动器两端的转换系数。利用这些参数,构造了矩阵形式的转换方程,并通过数值模拟验证了模型的合理性。

1 压电叠层作动器阻抗模型

1.1 作动器描述

图1为压电叠层作动器的结构示意图。作动器由很多压电片逐层叠放而成。各压电片用粘性材料粘接在一起,两片之间依次焊接有正负电极。这样,各压电片电压相同,而作动器的位移是每片压电片的位移之和。

为叙述方便,建立如图1所示的直角坐标系。作动器的两端分别处于z=0和z=tn位置。其中,t为压电片的厚度(假设厚度一致),n为压电片的层数。

图1 压电叠层作动器结构示意图

图2 作动器与外部结构的阻抗示意图

1.2 短路机械阻抗

短路机械阻抗是压电叠层作动器的机械属性,这是因为在短路条件下电压为零。这时作动器可以作为一个纯机械系统来处理。对于大多数的压电叠层作动器,只能承受轴向载荷。因此,本文只关注沿z方向的振动。粘接层和电极层的影响可通过改变压电材料的弹性模量来体现,因此不予考虑。基于这些假设,作动器可以看成一根均质连续的等截面直杆。

杆的纵向振动方程

(1)

其中:w为任意一点沿z方向的位移,c为波速:

(2)

分离变量,运动方程的解可表示成如下形式

w=(Asinλz+Bcosλz)ejωt

(3)

在文献[6]中,通过假设刚性壳体而得到固定-自由边界条件,从而B=0。然而,壳体往往由金属片制成,厚度有限,其阻抗不可能为无穷大。同时,压电叠层作动器通常会通过铰链或者万向节之类的隔离装置与主体结构相连,以免在压电片中产生弯矩而使其破碎。这些装置一般体量不大,其阻抗也是有限值。考虑到这些实际情况,采用两端自由边界条件。

根据机械阻抗的定义,作动器两端的轴向力与相应的速度可用下式描述

(4)

其中:负号表示正的位移(或者速度)产生压缩力。

假设压电片内的应力均匀分布,则有:

(5)

其中:Tz、F分别为某个压电片沿z方向的应力和力,Ap为压电片的横截面面积。

压电材料的本构方程为[11]

(6)

(7)

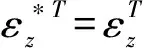
根据弹性体的本构关系,应变也可写成如下形式:

(8)

从方程(3)～(6)、(8)可解出未知量A和B

(9a)

(9b)

其中:Z11，Z12,Z22为作动器的机械阻抗

(10a)

(10b)

(10c)

其中:Z11，Z12分别为两端自由条件下的原点阻抗和跨点阻抗；Z22为固定-自由条件下的原点阻抗。

从而得到压电叠层作动器的短路机械阻抗矩阵[12]

(11)

显然,在利用该式计算轴向力或者速度时,需要同时考虑原点阻抗和跨点阻抗。

式(9)既包括了作动器的阻抗又包括了外部阻抗,而且外部阻抗的值可以是有限值,也可以是无穷大,因此是一个通用表达式。未知量A和B与外部阻抗的取值密切相关,下面讨论一些特殊情况。

工况1：作动器一端置于刚性地基上,另一端与柔性结构相连。在这种情况下,刚性基础的阻抗为无穷大而柔性结构的阻抗为有限值。对于作动器,这实际上对应于固定-自由边界条件。不妨假设Ze1=∞,代入式(9)可得

这正是文献[6]给出的结果。在这种情况下,短路机械阻抗矩阵将退化成一个标量,即Z=Z22。

工况2：作动器未连接到任何结构,即Ze1=Ze2=0。显然,这是理想的自由-自由边界条件。此时有

工况3：作动器两端均连接到一个刚性结构上。在这种两端固定条件下,作动器不会有任何位移,即w≡0。因此,A=B=0。

可以看出,对于后面两种情况,A、B中均未出现作动器的机械阻抗,这是因为不存在力或者速度。

1.3 电阻抗

在压电叠层作动器中,压电片逐层叠放,总位移是每片位移之和,即各压电片为串联关系。因此,推导机械阻抗时把作动器作为一根杆来处理。然而,施加于每片压电片的电压相同,即电学属性为并联,因此需要分别处理。基于此考虑,把式(7)写成如下形式

(12)

式(6)对任意一片压电片均成立。整理得

(13)

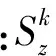
由式(3)、(8)可得第k层压电片的平均应变

(14)

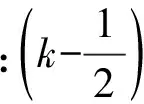
把式(14)代入式(13),再把结果代入式(12),有

(15)

利用下面的数学公式(式(16)),上式可简化为

(16a)

(16b)

(17)

一般情况下,流经压电片的电流密度只取决于压电片沿z方向的位置,而与坐标x、y无关。因此,流经压电片的电流(电流密度在压电片表面的积分)为

(18)

把式(9)代入式(17)和(18),可得作动器的电导纳,即电流与所施加电压之比

(19)

此式也是一个通用表达式,同时包含了作动器和外部结构的阻抗。根据外部阻抗的取值,对三种特殊情况进行类似的讨论。

工况1：Ze1=∞,Ze2为有限值。电导纳为

(20a)

与文献[6]在固定-自由条件下得到的表达式完全相同。

工况2：Ze1=Ze2=0。这种情况下得到的为自由电导纳

工况3：作动器两端固定,即外部结构的阻抗为无穷大。可以得到钳制电导纳

(20c)

如果只考虑一片压电片,即n=1,则式(20)可进一步简化。为便于比较,引入两个常用的定义式

其中:C为压电片的电容,k33为压电片的机电耦合系数。

利用这两个定义,式(20)可以写成

(21a)

(21b)

(21c)

这三个表达式均与压电理论基本公式[11]一致。而且,当ω→0时,tanλt/λt→1,式(21a)可简化成

这恰好就是准静态条件下压电片的电导纳,Liang等[3]，Giurgiutiu等[13]都描述或利用过这一公式。因此,式(19)可以看作是这些结果的通用表示。通过改变其中的参数可以揭示一些重要的现象或者事实。

根据阻抗的定义,即导纳的逆或者倒数,可以得到压电叠层作动器的电阻抗

(22)

1.4 转换系数

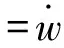
把式(9)代入式(3),并利用关系式E=U/t,可得

(23a)

(23b)

其中:φ1、φ2分别为作动器两端的转换系数。

一般情况下,作动器两端的速度均不为零,因此这两个转换系数都存在。这样,我们可以得到向量形式的转换系数:

(24)

式(23)也包含外部阻抗。同样讨论三种特殊情况。

工况1：Ze1=∞,Ze2为有限值。有

该式说明,在作动器的固定端,由于端面固定,即使有电压输入,位移和速度也为零。因此转换系数为零。同样地,在文献[6]中也给出了相同的结果。

工况2：Ze1=Ze2=0。对于这种情况,有

实际上,两个外部阻抗不管取何值(零或者非零),只要满足Ze1=Ze2,就可以得到φ2=-φ1的结论。根据前面的叙述可知,压电叠层作动器在z方向是对称的,如果外部阻抗相等,那么两端的约束条件也是对称的。这样,作动器在电场作用下的变形也是对称的,即两端的速度等值反向。所以φ2=-φ1。

工况3：作动器两端固定。这时作动器两端的位移和速度均为零,因此转换系数也为零。

1.5 转换方程

如前所述,压电元件与主体结构之间由于压电效应而相互耦合。在研究机电耦合特性方面,转换方程是比较有效的。转换方程有多种表达形式,下面的互易形式是最方便的[11]

(25)

(26)

机械阻抗、电阻抗以及转换系数的表达式在前面各节中已经给出。剩下的四个变量中,如果已经知道两个,比如已知力和电压,则通过这两个方程可求出另外两个变量。应该指出,力和速度一般情况下是包含两个元素的向量,因此式(25)实际上是矩阵方程。

值得一提的是,前面所有的推导都是针对压电叠层作动器本身的。封装压电片所用的壳体、预紧弹簧、输出杆以及被控结构等外部结构所产生的影响都包含在外部阻抗中。对于一个具体的作动器,可以根据这些结构的连接形式,利用下述公式得到外部阻抗

其中:Z为总阻抗,Zi为每个子结构的阻抗。这两个公式分别用于并联和串联。

2 数值模拟

为验证模型的正确性,并研究外部阻抗对这些参数的影响,以上述公式为基础,进行了数值模拟。为便于比较,选用文献[6]中使用的材料属性,列于表1中。

表1 压电作动器材料属性[6]

图3所示为压电叠层作动器的机械阻抗随频率的变化曲线。可以看出,随着频率的增加,不同边界条件下的原点阻抗表现出不同的变化规律。两条曲线关于某条水平线对称。在某一频率上,一个(两端自由情况)处于反共振状态,而另一个(固定-自由情况)则处于共振状态。这一点亦可从式(10)得出,即当Z11=0时，Z22→∞,反之亦然。至于两端自由条件下的跨点阻抗,其幅值随频率的变化则不像这两个阻抗那么剧烈,在图示频率范围内,既没有共振也没有反共振。

图4给出的是外部阻抗对电阻抗的影响。图例中的数值为外部阻抗之比,即Ze1/Ze2。图5和图6中图例与此相同。当两个外部阻抗恰好相等时,在较高的频率(大约10 kHz)处出现共振。然而,如果两个阻抗不相等,第一阶共振频率则急剧降低,而且在图示频率范围内出现两个共振频率。随着阻抗比的增大,这两个共振频率相互靠近。当一个阻抗远远大于另外一个时,两个共振频率合并为一个。这时的曲线(图中的实线)与文献[6]中所描述的完全一致。

图3 机械阻抗的幅值随频率的变化

图4 电阻抗的幅值随频率的变化

如前所述,压电叠层作动器为对称结构,若外部阻抗也相同,则作动器的变形是对称的,即作动器中部将保持静止不动。这时,整个作动器可看成是由两个具有固定-自由边界的作动器以背靠背的方式串联而成。而当两个外部阻抗相差非常大时,则是整个作动器两端的约束为固定-自由条件,因此在较低的频率(大约6 kHz)处出现共振。

从图5中可以看出,外部阻抗对转换系数φ2有类似的影响。当两个阻抗相等时,共振频率较高；二者不等时,在较低频率出现两个共振频率。随着阻抗比的增大,两个共振频率互相靠近,最终合并成一个。不过,转换系数与电阻抗随频率的总体变化趋势不同——随着频率增加,电阻抗基本上是减小的,而转换系数基本上是增大的。

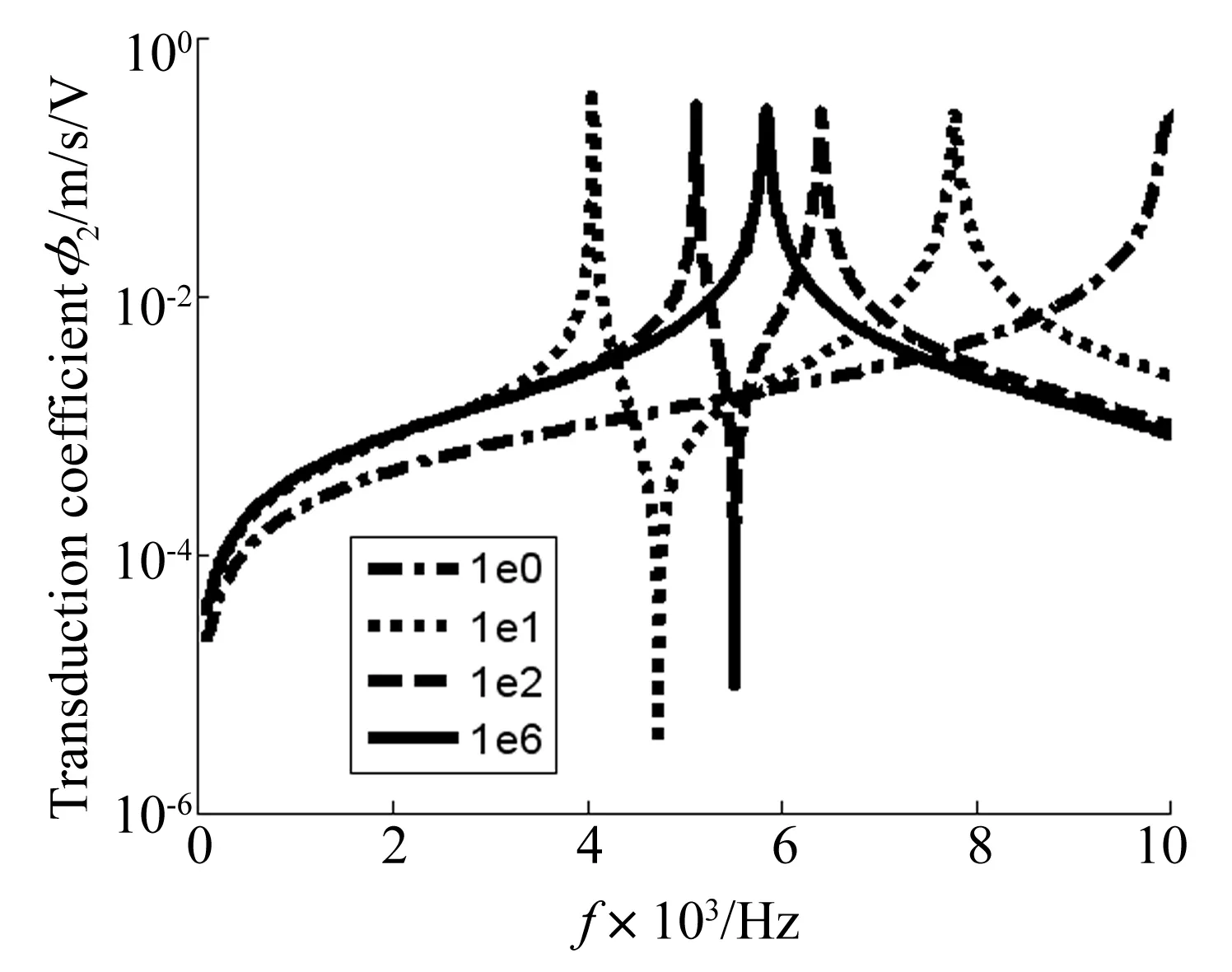
图5 转换系数φ2的幅值随频率的变化

图6 转换系数φ1的幅值随频率的变化

对比图6和图5,可以发现转换系数φ1随频率的变化与φ2类似,但有两点明显的不同。首先,较低的共振频率随阻抗比的增大而增大,但第一阶反共振频率却保持不变。其次,随着阻抗比的增大,转换系数φ1迅速减小。这就意味着当外部阻抗足够大时,此处的位移和速度将非常小,可近似为固定边界条件。

3 结 论

以阻抗法为基础,采用更接近于实际的两端自由杆的纵向振动方程,建立了压电叠层作动器的机电耦合模型。在短路机械阻抗矩阵中,不仅包括了原点阻抗,还考虑了两端之间的跨点阻抗。与之相适应,作动器两端的转换系数也以向量的形式给出。同时推导出更具一般意义的电阻抗表达式。以这些参数为基础,构建了矩阵形式的转换方程。研究发现：

(1)不同边界条件下的短路机械阻抗表现出不同的特点。原点阻抗与跨点阻抗的特点也不同。

(2)作动器两端的外部阻抗对电阻抗和转换系数有重要影响。当两个外部阻抗相同或者差别非常大时,作动器两端的边界条件可视为固定-自由条件。此时,短路机械阻抗、电阻抗和转换系数的表达式可大大简化。其它情况则需考虑外部阻抗的影响。

(3)作动器两端的转换系数不同。如果某端的外部阻抗足够大,该处的转换系数则会接近于零。

(4)本文开发的模型可用于振动主动控制以及其它应用,相关研究将在后续论文中讨论。

[1]Crawley E F，Deluis J.Use of piezoelectric actuators as elements of intelligent structures[J].AIAA Journal，1987,25(10):1373-1385.

[2]Ha S K,Chang F K,Keilers C.Finite element analysis of composite structures containing distributed piezoceramic sensors and actuators [J].1992，AIAA Journal，30(3): 772-780.

[3]Liang C，Sun F P，Rogers C A.An impedance method for dynamic analysis of active material system [J].Journal of Vibration and Acoustics，1994，116(1):121-128.

[4]Cheng C C，Wang P W.Applications of the impedance method on multiple piezoelectric actuators driven structures [J].Journal of Vibration and Acoustics，2001，123(2)，262-268.

[5]Annamdas V G M，Soh C K.Three-dimensional electromechanical impedance model: formulation of directional sum impedance[J].Journal of Aerospace Engineering，2007，20(1)，53-62.

[6]Flint E M，Liang C，Rogers C A.Electro-dynamic transduction equations for piezoelectric stack actuator[C].// International Mechanical Engineering Congress and Exposition，Chicago，November,1994，45:201-210.

[7]李俊宝，吕刚.智能桁架结构振动控制中压电主动构件的研究: (三)压电主动构件动力学建模[J].压电与声光,1998，20(4):237-241.

LI Jun-bao，LÜ Gang.Research on piezoelectric active member in vibration control of intelligent truss structure: (3)dynamic modeling of piezoelectric active member[J].Piezoelectrics & Acoustooptics,1998，20(4):237-241.

[8]郑凯,阎绍泽,温诗铸,等.预压力对压电叠层作动器性能的影响 [J].压电与声光，2003，25(5): 363-365.

ZHENG Kai，YAN Shao-ze，WEN Shi-zhu，et al.Influence of preload on the piezoelectric for piezoelectric stack actuator[J].Piezoelectric & Acoustooptics，2003，25(5): 363-365.

[9]Wang W，Yang Z C.A compact piezoelectric stack actuator and its simulation in vibration control [J].Tsinghua Science and Technology，2009，14(S2): 43-48.

[10]靳宏,金龙,徐志科,等.压电叠堆位移放大致动器的动态特性[J].振动与冲击，2012，31(21): 146-151.

JIN Hong，JIN Long，XU Zhi-ke，et al.Dynamic characteristics of a piezoelectric-stack displacement-amplifying actuator [J].Journal of Vibration and Shock，2012，31(21): 146-151.

[11]Ikeda T.Fundamentals of piezoelectricity[M].London: Oxford University Press，1990.

[12]Bishop R E D，Johnson D C.The mechanics of vibration[M].London: Cambridge University Press，2011.

[13]Giurgiutiu V，Anderi N Z.Embedded self-sensing piezoelectric active sensors for on-line structural identification[J].Journal of Vibration and Acoustics，2002，124(1): 116-125.