丢番图方程x2-3y4=397的正整数解

李 伟

(兰州交通大学 数理与软件工程学院， 甘肃 兰州 730070)

丢番图方程x2-3y4=397的正整数解

李 伟

(兰州交通大学 数理与软件工程学院， 甘肃 兰州 730070)

利用递归序列、同余式、二次剩余的方法证明了丢番图方程x2-3y4=397仅有正整数解(x,y)=(20,1)。

丢番图方程； 递归序列； 二次剩余； 正整数解

0 引 言

关于丢番图方程x2-Dy4=N(D，N∈Z，且D>0为非平方数)已有不少研究工作[1-7]。设N(D,N)为方程x2-Dy4=N的正整数解的组数，文献[1]证明了以下几个结果：

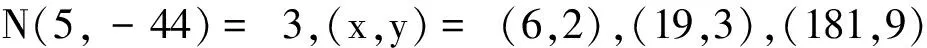
文献[3]证明了

文献[6]证明了当y≡0(mod8)时，

N(2,17)=0

N(2,41)=0

N(2,97)=0

N(8,17)=0

文中利用递归序列、同余式和二次剩余的方法证明了丢番图方程x2-Dy4=N,当(D,N)=(3,397)时仅有正整数解(x,y)=(20,1)。

1 定理及证明

定理丢番图方程

(1)

仅有正整数解(x,y)=(20,1)。

证明 首先考虑pell方程

(2)

其一般解由以下两个非结合类给出：

(3)

或

(4)

y2=±(vn+20un)

或

当n≥0时，vn+20un>0；当n<0时，vn+20un<0。因此可归结为

(5)

或

(6)

可验证下列关系成立:

(7)

(8)

(9)

对式(5)取模5,得剩余序列周期为3，当n≡1,2(mod3)时，vn+20un≡2(mod5),为模5的二次非剩余，故排除。剩n≡0(mod3)。

对式(5)取模3,得剩余序列周期为6，当n≡3,4(mod6)时，vn+20un≡2(mod3),为模3的二次非剩余，排除。剩n≡0,1,2,5(mod6)。

对式(5)取模7,剩余序列周期为8，当n≡2,4,5,7(mod8)时，vn+20un≡3,6,6,3(mod7),为模7的二次非剩余，排除。剩n≡0,1,3,6(mod8)。

对式(5)取模193,剩余序列周期为24，当n≡1,2,3,5,6,8,10,13,14,15,17,18,20,22(mod24)时，vn+20un≡22,87,133,103,160,58,73,171,106,60,90,33,135,120(mod193),为模193的二次非剩余,排除。剩n≡0,4,7,9,11,12,16,19,21,23(mod24)。

因此可归结为n≡0(mod24)。

若n≠0，令n=0+6(4k±1)m, m=2t, t>1, 由式(9)可知

(10)

因v2m≡2(mod5),所以

又v2m≡1(mod8)，设2s‖um，则

所以

因此

所以式(10)不成立，此时式(5)无解。当n=0时，得到方程(1)的解为(20,1)。

对式(6)取模5，剩余序列周期为3，当n≡1,2(mod3)时，-vn+20un≡3(mod5),为模5的二次非剩余,排除。剩n≡0(mod3)。

对式(6)取模3,剩余序列周期为6,当n≡0,5(mod6)时，-vn+20un≡2(mod3),为模3的二次非剩余,排除。剩n≡1,2,3,4(mod6)。结合模5得n≡3(mod6),即n≡3,9,15,21(mod24)。

对式(6)取模8,剩余序列周期为4,当n≡0(mod4)时，-vn+20un≡7(mod8),为模8的二次非剩余,排除；当n≡1,3(mod4)时，-vn+20un≡2(mod8)不可能为完全平方数,故排除。剩n≡2(mod4)，即n≡2,6,10,14,18,22(mod24)。所以式(6)无解。

由上述讨论可知，方程(1)仅有正整数解(x,y)=(20,1)。证毕。

[1]CohnJHE.Somequarticdiophantineequations[J].PacificJMath.,1968,26:233-243.

[2] Mordell L J. Diophantine equations[M]. London: Academic Press,1969.

[3] 曹珍富.丢番图方程引论[M].哈尔滨：哈尔滨工业大学出版社，2012.

[4] 朱德辉.关于不定方程x2-3y4=166[J].重庆师范大学学报:自然科学版，2008,25(3)：21-23.

[5] 黎进香，张春蕊.关于不定方程x2-3y4=46的初等解法[J].哈尔滨工业大学学报，1995,27(5)：13-16.

[6] Tzanakis N. On the diophantine equations[J]. Number Theory,1983,17:144-164.

[7] 柯召，孙琦.数论讲义[M].北京：高等教育出版社，2001.

Positive integer solutions of diophantine equationx2-3y4=397

LI Wei

(College of Physics and Software Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

Methods of recurrent sequence, congruence and quadratic residue are used to prove that diophantine equationx2-3y4=397 has positive integer solution (x,y)=(20,1) only.

diophantine equation; recurrent sequence; quadratic residue; positive integer solution.

2014-06-09

李 伟(1982-)，男，汉族，甘肃庆阳人，兰州交通大学硕士研究生，主要从事数论方向研究,E-mail:SLXYLiWei@163.com.

O 156.1

A

1674-1374(2014)06-0625-03