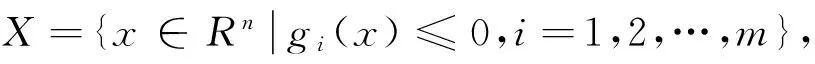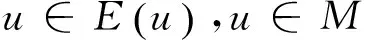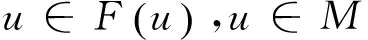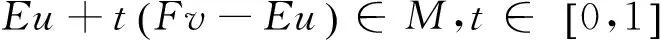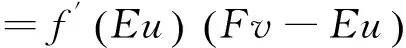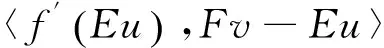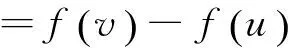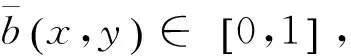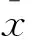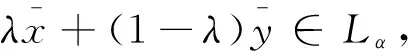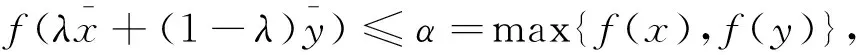半(E,F)-凸函数的一些新性质

马晓娜

宿州学院数学与统计学院，安徽宿州，234000

半(E,F)-凸函数的一些新性质

马晓娜

宿州学院数学与统计学院，安徽宿州，234000

基于(E,F)-凸函数，得到了半(E,F)-凸函数。引入次线性函数，利用半(E,F)-凸函数的定义，研究了次线性函数与半(E,F)-凸函数复合后的半(E,F)-凸性，半(E,F)-凸函数水平集的性质；研究了在半(E,F)-凸性的条件下极小值点存在的充要条件，并从变分不等式的角度对该充要条件作了全新的证明，且给出了另一个等价条件。

(E,F)-凸集;(E,F)-凸函数;半-凸函数;拟半(E,F)-凸数

1 基本概念

定义1[1]称集合M⊆Rn是(E,F)-凸集,若存在E,F:M→Rn使得对于∀x,y∈M,λ∈[0,1],有λE(x)+(1-λ)F(y)∈M。

定义2[1]称f:M→R为在M⊆Rn上的(E,F)-凸函数,若存在E,F:M→Rn使得M是(E,F)-凸集,且对于∀x,y∈M，λ∈[0,1],有:

f(λE(x)+(1-λ)F(y))≤λf(E(x)+(1-λ)F(y))

定义3[2]称f:M→R为M⊆Rn上的半(E,F)-凸函数,若存在E,F:M→Rn使得M是(E,F)-凸集,且对于∀x,y∈M,λ∈[0,1],有:

f(λE(x)+(1-λ)F(y))≤λf(x)+(1-λ)f(y)

定义4[2]称函数f:M→R为(E,F)-凸集M⊆Rn上的拟半(E,F)-凸函数,若∀x,y∈M,有:

f(λE(x)+(1-λ)F(y))≤max{f(x),f(y)},∀x,y∈M,λ∈[0,1]

定义5[3]函数f:Rn→R称为正齐次函数，如果对每个x都有:

f(λx)=λf(x), 0<λ<∞

(1)∀x∈X，∀t>0,f(tx)=tf(x);(2)∀x1,x2∈X,f(x1+x2)

2 主要结论

性质1 若f:M→R是(E,F)-凸集M上的半(E,F)-凸函数,φ:R→R是一非减次线性函数,那么复合函数h=φ∘f:M→R是M上的半(E,F)-凸函数。

证明 因为f:M→R是(E,F)-凸集M上的半(E,F)-凸函数,则对∀x,y∈M,λ∈[0,1]有映射E,F:M→Rn,使得：

f(λE(x)+(1-λ)F(y))<λf(x)+(1-λ)f(y)

又φ:R→R是非减次线性函数,故：

φ∘f(λE(x)+(1-λ)f(y))<φ[λf(x)+(1-λ)f(y)]<λφ∘f(x)+(1-λ)φ∘f(y)

所以,复合函数h=φ∘f:M→R是半(E,F)-凸函数。

性质2f(x)是正齐次函数,E,F是正齐次映射,且f(E(x)+F(y))

证明 ∀x,y∈M,λ∈[0,1]

因为f(E(x)+F(y))

性质3 设f:M⊆Rn→R在(E,F)-凸集M上是可微的半(E,F)-凸函数，u∈M是一确定点，且有u=Eu,u=Fu，则u∈M是f在M上的极小点，当且仅当满足下列不等式：

〈f′(Eu),Fv-Eu〉≥0∀v∈M

这里f′(Eu)是f在Eu处的微分。

下面从变分不等式的角度对性质3给予一全新的证明，并给出另一个等价条件。

设f:M⊆Rn→R在(E,F)-凸集上是可微的半(E,F)-凸函数，u∈M是一确定点，且有u=Eu,u=Fu，则下述结论是等价的。

(1)u∈M是f在M上的极小点；

证明 (1)⟹(2)：

即

(2)⟹(1)：

由于

所以对于上式，令t→0，得：

(2)⟹(3):

对于不等式

f(v)-f(u)≥〈f′(Eu),Fv-Eu〉

(a)

交换Eu,Fv得：

f(u)-f(v)≥〈f′(Fv),Eu-Fv〉

(b)

(a)、(b)两式相加得：

〈f′(Fv)-f′(Eu),Fv-Eu〉≥0

即〈f′(Fv),Eu-Fv〉≥〈f′(Eu),Fv-Eu〉≥0

(3)⟹(2)：

因为〈f′(Fv),Eu-Fv〉≥0∀v∈M，用Eu+t(Fv-Eu),t∈[0,1]代替Fv得：

〈f′(Eu+t(Fv-Eu)),t(Fv-Eu)〉≥0

即〈f′(Eu+t(Fv-Eu)),(Fv-Eu)〉≥0

又因为f可微，则f在t=0处右连续，令t→0+得：

〈f′(Eu),Fv-Eu〉≥0，∀v∈M

性质4 如果f为(E,F)-凸集M上的拟半(E,F)-凸函数，则对∀α∈R，定义f的水平集为Lα，且Lα={x:x∈M,f(x)α∀α∈R}，则：

(1)Lα为(E,F)-凸集；

(2)集合Lα是一个(E,F)-凸集，则f是M上的拟半(E,F)-凸函数。

证明 (1)∀x,y∈Lα，有f(x)≤α,f(y)≤α，又因为f为M上的拟半(E,F)-凸函数，所以有：

(2)∀x,y∈M令α=max{f(x),f(y)}，则：

f(x)≤α,f(y)≤α

即x∈Lα,y∈Lα

又集合Lα是一个(E,F)-凸集，则λ∈(0,1)，有：

[1]Jian J B．On(E,F)generalized convexity[J]．International Journal of Mathematical sciences,2003,1(2)：121-132

[2]Jian J B．Hu Q J．Tang C M．et al．Semi-(E,F)-convex functions.and Semi(E,F)programming[J]．International Journal of Pure and Applied Mathematics,2004，4(14)：439-454

[3]胡清洁，梁远信，简金宝.一类新的广义凸函数及相应的凸规划的最优性条件与对偶[C]//中国运筹学会第七届学术交流会论文集：上卷.青岛：中国运筹学会，2004

(责任编辑：汪材印)

SomeNewPropertiesofSemi-(E,F)-ConvexFunctions

MAXiao-na

SchoolofMathematicsandStatistics，SuzhouUniversity，SuzhouAnhui,234000,China

Based on the(E,F)-convex function,the semi-(E,F)-convex function is obtained, in order to further improve the properties of semi-(E,F)-convex function, the application of semi-(E,F)-convex function is defined constraints reduce,research which can be better applied in optimization problems. Firstly,introduced a linear function, using the definition of semi-(E,F)-convex function,studied the linear function and after the semi-(E,F)-convex function composite semi-convexity,the properties of semi-(E,F)-convex function of the level set,and studied under the condition of semi-(E,F)-convex sufficient and necessary condition for the existence of minimum point. In order to obtain the necessary and sufficient conditions for existence of the minimum point,make a new proof of the necessary and sufficient conditions of the variational inequality,and another equivalent condition is given.

(E,F)-convex set;(E,F)-Convex functions; semi-(E,F)-convex functions; quasi-semi-(E,F)-convex functions.

2014-04-18

马晓娜(1982-)，女，辽宁鞍山人，硕士，助教，主要研究方向：最优化理论及其应用研究。

10.3969/j.issn.1673-2006.2014.09.022

O174.13

A

1673-2006(2014)09-0074-03