超临界二氧化碳扩散行为的分子动力学模拟

，， ，，

(1.大连理工大学 化工学院，辽宁 大连 116024；2.大连理工大学 化机学院，辽宁 大连 116024)

•开发与研究•

超临界二氧化碳扩散行为的分子动力学模拟

王宝和1，杨刘玮1，李群1，夏良志2，王刚1

(1.大连理工大学 化工学院，辽宁 大连 116024；2.大连理工大学 化机学院，辽宁 大连 116024)

二氧化碳分子选用EPM2模型，乙醇分子选用TraPPE-UA模型，采用分子动力学模拟技术，探讨了超临界二氧化碳的自扩散系数及乙醇—超临界二氧化碳体系的无限稀互扩散系数。模拟结果表明，超临界二氧化碳的自扩散系数和乙醇—超临界二氧化碳体系的无限稀互扩散系数均随着温度的升高或压力的降低而增大。

分子动力学；超临界二氧化碳；扩散系数；模拟

超临界二氧化碳的扩散系数与其许多物性参数相互关联，是科学研究、工程开发和过程设计不可缺少的基础数据。鉴于超临界二氧化碳分子间相互作用的复杂性，完全从理论上进行准确预测仍存在较大的难度；苛刻的测试条件使得超临界二氧化碳扩散系数的实验测定十分困难。随着计算机和分子动力学(MD)模拟技术的发展，从分子水平研究超临界二氧化碳的扩散规律，已经引起国内外许多学者的极大关注[1-3]。俞联梦等[4]采用MD模拟方法，探讨了CO2-水体系的PVT性质、扩散系数、微观结构、配位数及氢键作用。Higashi等[5]利用MD模拟了纯CO2流体和CO2-萘混合体系的CO2扩散系数。Colina等[6]采用Monte Carlo模拟技术，计算了超临界CO2的密度、焦耳—汤普森系数、等压热容、等温压缩系数等物性参数。Zhou等[7]利用MD模拟方法，探究了超临界二氧化碳中有机物的扩散行为，并提出一个新的计算二氧化碳无限稀互扩散系数方程。本文拟采用MD模拟技术，研究超临界二氧化碳的自扩散系数及乙醇—超临界二氧化碳体系的无限稀互扩散系数。

1 模拟方法

1.1二氧化碳及乙醇的势能模型

二氧化碳分子模型有很多，如MSM、EPM2、TraPPE等。本研究的二氧化碳选用EPM2模型，其分子结构和势能参数如图1和表1所示。

图1 二氧化碳分子的结构示意图

其中σC-C为C原子之间L-J势能的尺度参数，σO-O为O原子之间L-J势能的尺度参数，εC为C原子之间L-J势能的能量参数，εO为O原子之间L-J势能的能量参数，kB为Boltzmann常数(kB=1.380 6×10-23J/K )，rC-O为C原子与O原子之间的键长，θ为键角，qO和qC分别为二氧化碳分子中O原子和C原子所带电荷，e为基本电荷(1e=1.6×10-19C)。

表1 二氧化碳分子的结构参数[8]

乙醇分子模型有全原子模型和联合原子模型等。由于全原子模型的计算耗时较长，一般采用联合原子模型。乙醇分子的联合原子模型有OPLS-UA和TraPPE-UA模型，本研究的乙醇分子选用TraPPE-UA模型，其分子结构及其参数见图2和表2。该模型有四个作用位点，分别为甲基CH3(1号C原子)、亚甲基CH2(2号C原子)、O原子和H原子，各个作用位点的相关势能参数见表3。

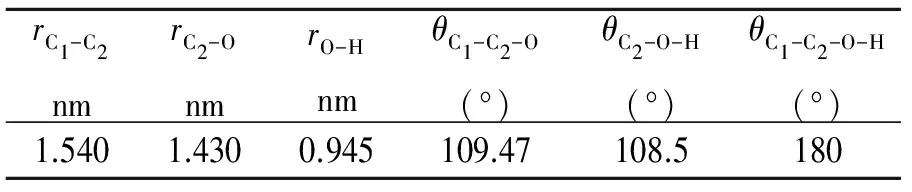
表2 乙醇分子的结构参数[9]

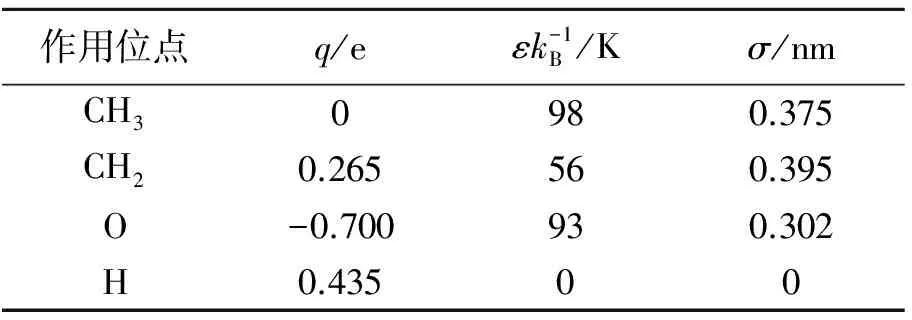
表3 TraPPE-UA模型参数

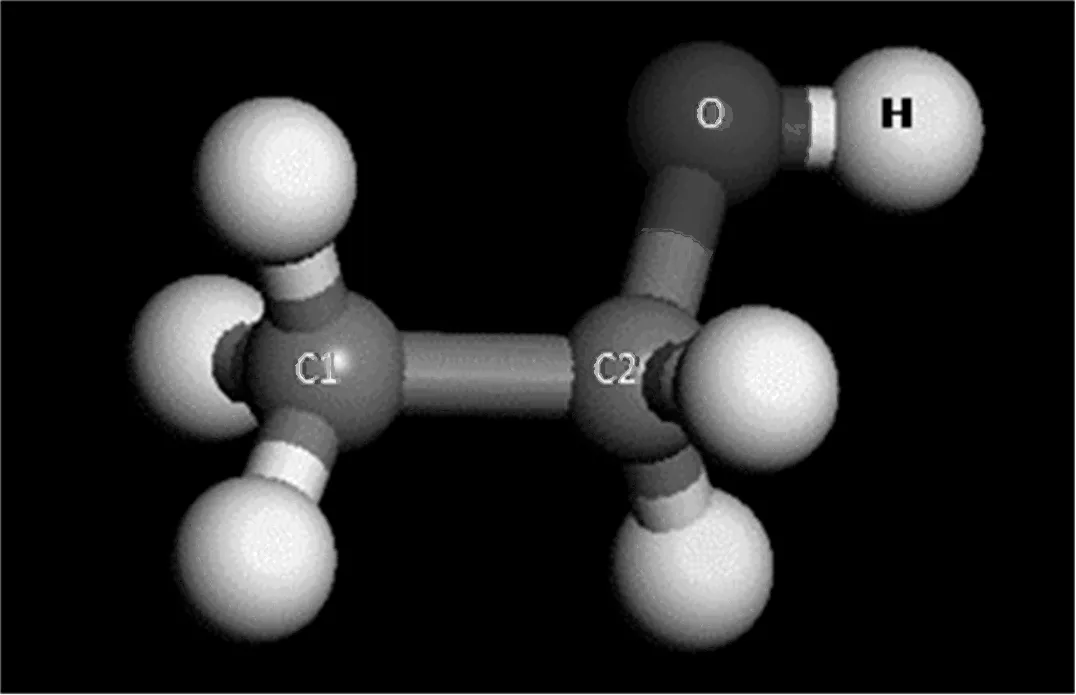
图2 乙醇分子的结构示意图

其中rC1-C2为1号C原子与2号C原子之间的键长；rC2-O为2号C原子与O原子之间的键长；rO-H为O原子与H原子之间的键长；θC1-C2-O为1号C原子、2号C原子及O原子组成的键角；θC2-O-H为2号C原子、O原子及H原子组成的键角；θC1-C2-O-H为1号C原子、2号C原子、O原子及H原子之间形成的二面角。

在进行超临界二氧化碳的自扩散系数及乙醇—超临界二氧化碳体系的无限稀互扩散系数的MD模拟过程中，每个分子(包括二氧化碳分子和乙醇分子)被视为刚性结构，忽略分子内的作用势能，只考虑分子间作用势能，分子间的势能函数如式(1)～(3)所示[10]。

U=Ue+ULJ

(1)

(2)

(3)

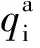
两种不同粒子间的L-J势能参数，用Lorentz-Berthelot规则计算，如式(4)所示。

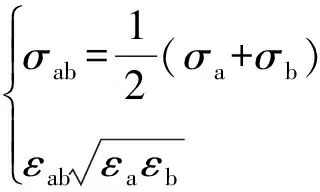
(4)

对于短程L-J势能函数，为了避免计算过程中由于边界位置的不连续，导致Hamiltonian函数的不守恒，从而引起误差，因此采用势能截断的方法来处理此问题，如式(5)所示[11]。

(5)

采用作用场法来处理长程静电势能。将静电力分为两部分，位于截断半径内的计算所有电荷间的库伦静电力，将截断半径外的库伦作用看作介电常数为εs的均匀介质对电荷的作用。依照作用场法，长程静电势能可表示为式(6)[11]。

Ue=

(6)

通常，环境介电常数εs取无穷大，因此，式(6)可简化为式(7)

Ue=

(7)

1.2模拟体系的建立

1.2.1 超临界二氧化碳自扩散的模拟体系

将超临界二氧化碳分子的初始结构按照面心立方(FCC)的形式均匀排布于边长为L的立方体盒子里，L的大小由一定的温度和压力下超临界二氧化碳的实验密度来确定。且体系的质心位于盒子中心处。如图3所示。

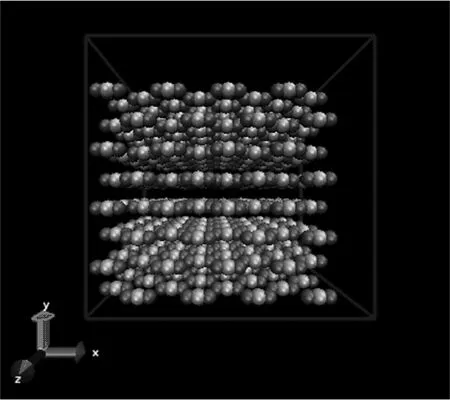
图3 超临界二氧化碳自扩散的模拟体系示意图

1.2.2 乙醇—超临界二氧化碳无限稀互扩散的模拟体系

对于溶质乙醇在溶剂超临界二氧化碳中的二元混合体系，无限稀意味着溶质乙醇分子四周几乎都充满了溶剂超临界二氧化碳分子。在工程实际计算中，当溶质浓度达到5%，甚至10%时，仍可按照无限稀状态进行计算。在本文的MD模拟中，为了实现无限稀状态，模拟体系的总分子数为256，其中乙醇分子数为1，超临界二氧化碳分子数为255，初始结构为面心立方(FCC)结构，如图4所示。由于整个体系为无限稀状态，我们假设乙醇分子的引入不影响整个体系的密度及体积，因此，立方体的边长L仍由一定温度T和压力p下超临界二氧化碳的实验密度来确定。

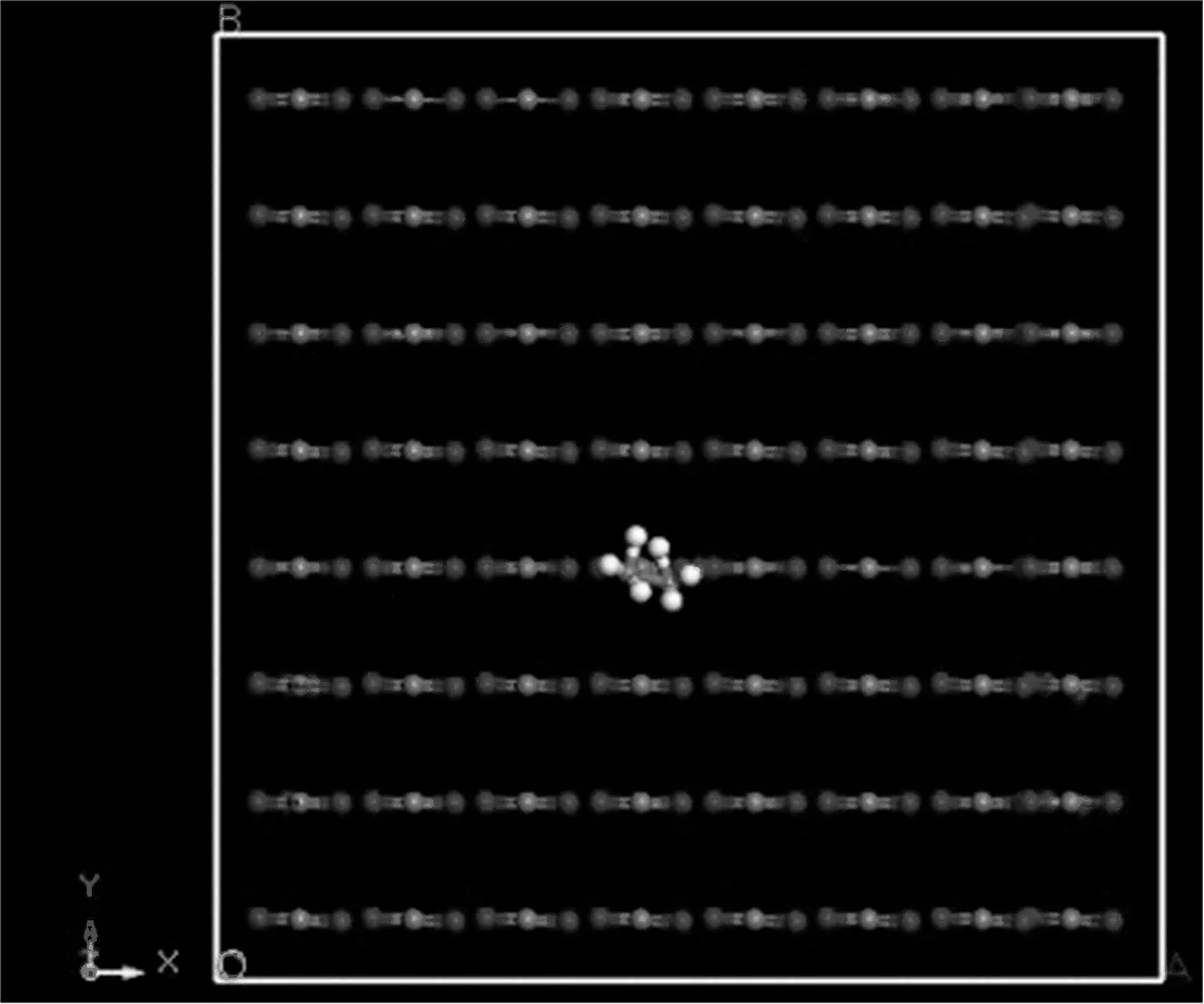
图4 乙醇—二氧化碳无限稀互扩散的模拟体系示意图

1.3模拟细节

本模拟在x、y、z三个方向上均采用周期性边界条件；模拟时间步长为1 fs，总模拟时间为1 000 ps，前500 ps使得系统达到平衡，后500 ps统计计算并输出系统的均方位移MSD。选取正则系综(NVT)，并采用Woodcock控温法维持体系温度的恒定；依照设定的温度，随机分布分子的初始平动速度；为了保证系统的总动量为0，每隔1万步矫正体系的质心，使之始终处于盒子的中心处；本文模拟数据均采用LAMMPS(Large-scale Atomic/Molecular Massively Parallel Simulator)软件计算得到。

2 结果与讨论

2.1超临界二氧化碳的自扩散系数

2.1.1 超临界二氧化碳自扩散系数的确定方法

采用Einstein法，计算超临界二氧化碳自扩散系数的方程，如式(8)所示[12]。

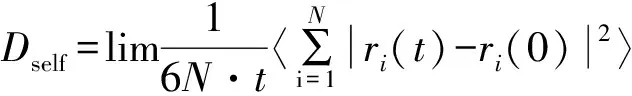
(8)

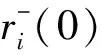
根据MD模拟的计算结果，利用方程(9)可计算出均方位移(MSD)。

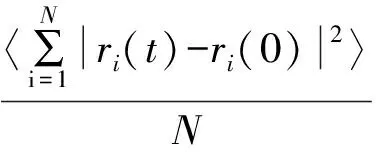
(9)

根据方程(8)和(9)，可得式(10)。

(10)

由式(10)可见，当模拟时间t很长时，MSD与时间t的关系曲线应该为一条直线，根据其斜率可求得自扩散系数。

在二氧化碳分子数N=256，温度T=323 K，压力p=10.99 MPa的条件下，MD模拟得到的均方位移(MSD)随时间t的变化及线性拟合曲线，如图5所示。可见，均方位移(MSD)与时间t具有很好的线性关系，从而得到超临界二氧化碳的自扩散系数Dself=5.634×10-8m2/s。

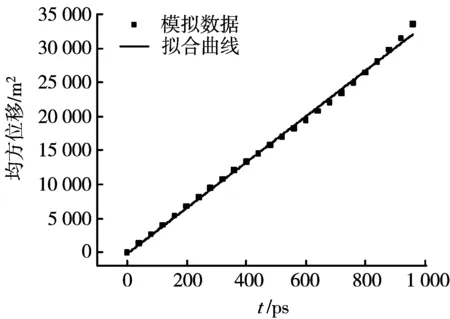
图5 均方位移与时间关系曲线

2.1.2 压力对二氧化碳自扩散系数的影响

在二氧化碳分子数N=256，T=323 K的条件下，MD模拟得到的二氧化碳自扩散系数与压力之间的关系曲线，并与文献值[13]进行了比较，如图6所示。由图6可见，二氧化碳的自扩散系数随着压力的升高而减小；在低密度的亚临界区，流体很容易被压缩，扩散系数随着体系压力的升高而快速减小；在靠近临界点附近，二氧化碳分子的扩散系数对体系压力的变化也很敏感；当体系压力大于15 MPa时，随着压力的升高，二氧化碳的自扩散系数变化缓慢，呈现出液体的特性。

图6 不同压力下二氧化碳自扩散系数的MD模拟结果

2.1.3 温度对二氧化碳自扩散系数的影响

在二氧化碳分子数N=256，压力p=8 MPa的条件下，MD模拟得到的二氧化碳自扩散系数与温度之间的关系曲线，并与文献值[14]进行了比较，如图7所示。由图7可知，随着温度的升高，二氧化碳自扩散系数增大，并在不同的温度段展现出不同的增大速度；当温度较低时，即T<300 K，模拟系统为液相，随着温度的升高，自扩散系数增大比较缓慢，当T>300 K时，随着温度的升高，自扩散系数显著增大，并在临界点附近有明显的转折点；可见，在超临界状态下，二氧化碳分子具有较强的扩散能力。

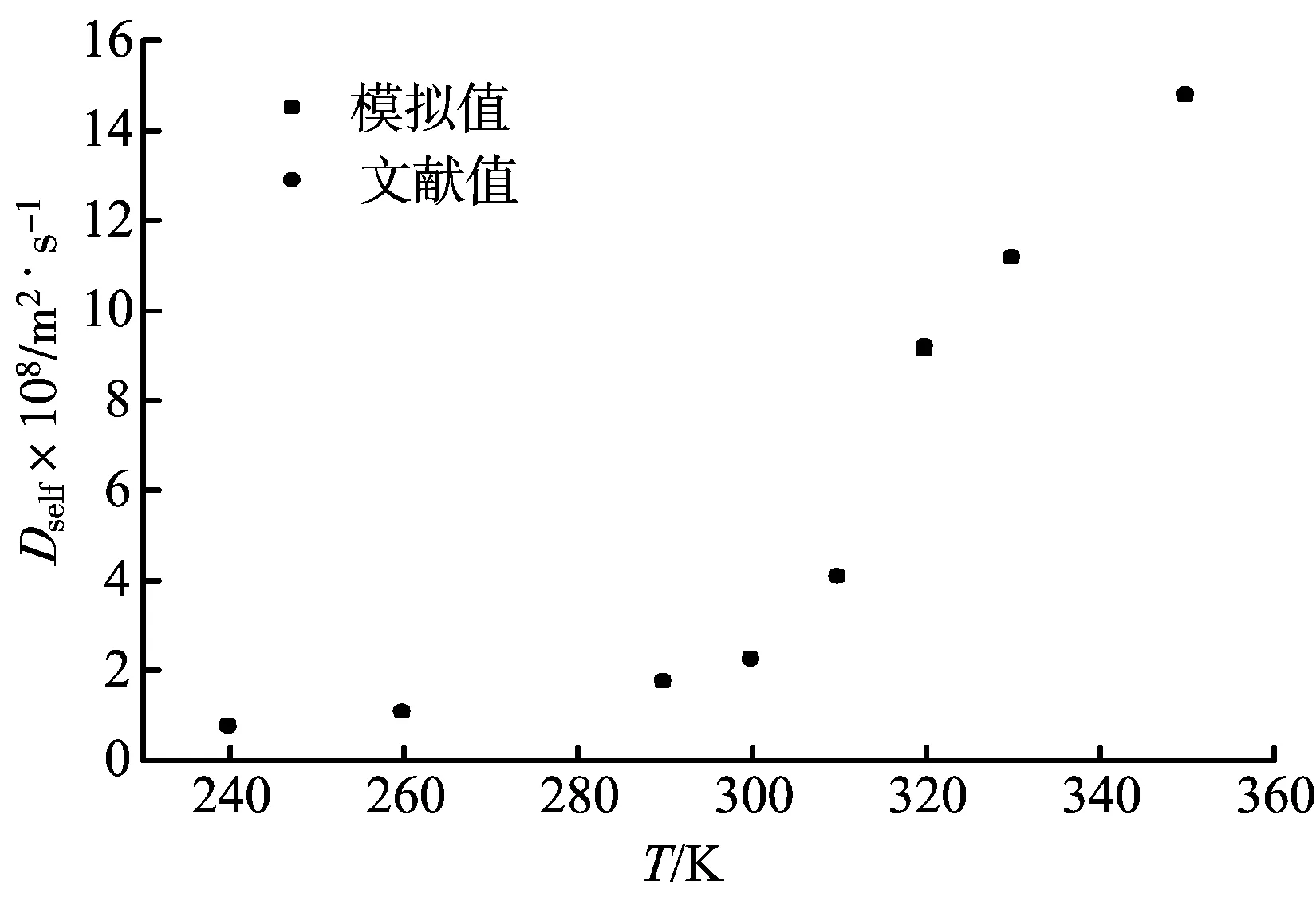
图7 不同温度下二氧化碳自扩散系数的MD模拟结果

2.2乙醇—超临界二氧化碳体系的无限稀互扩散系数

2.2.1 乙醇—超临界二氧化碳无限稀体系的互扩散系数确定方法

采用Einstein法，确定乙醇—超临界二氧化碳无限稀体系的互扩散系数，如式(11)所示[12]。

(11)

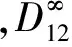
与自扩散系数确定方法类似，根据MD模拟的计算结果，可计算出均方位移(MSD)，再由MSD与时间t关系曲线的斜率可求得无限稀互扩散系数。

在温度T=323 K，压力p=8.41 MPa，二氧化碳分子数为255，乙醇分子数为1的条件下，MD模拟得到的均方位移(MSD)随时间t的变化及线性拟合曲线，如图8所示，从而得到乙醇—超临界二氧化碳无限稀体系的互扩散系数D12=6.048×10-8m2/s。

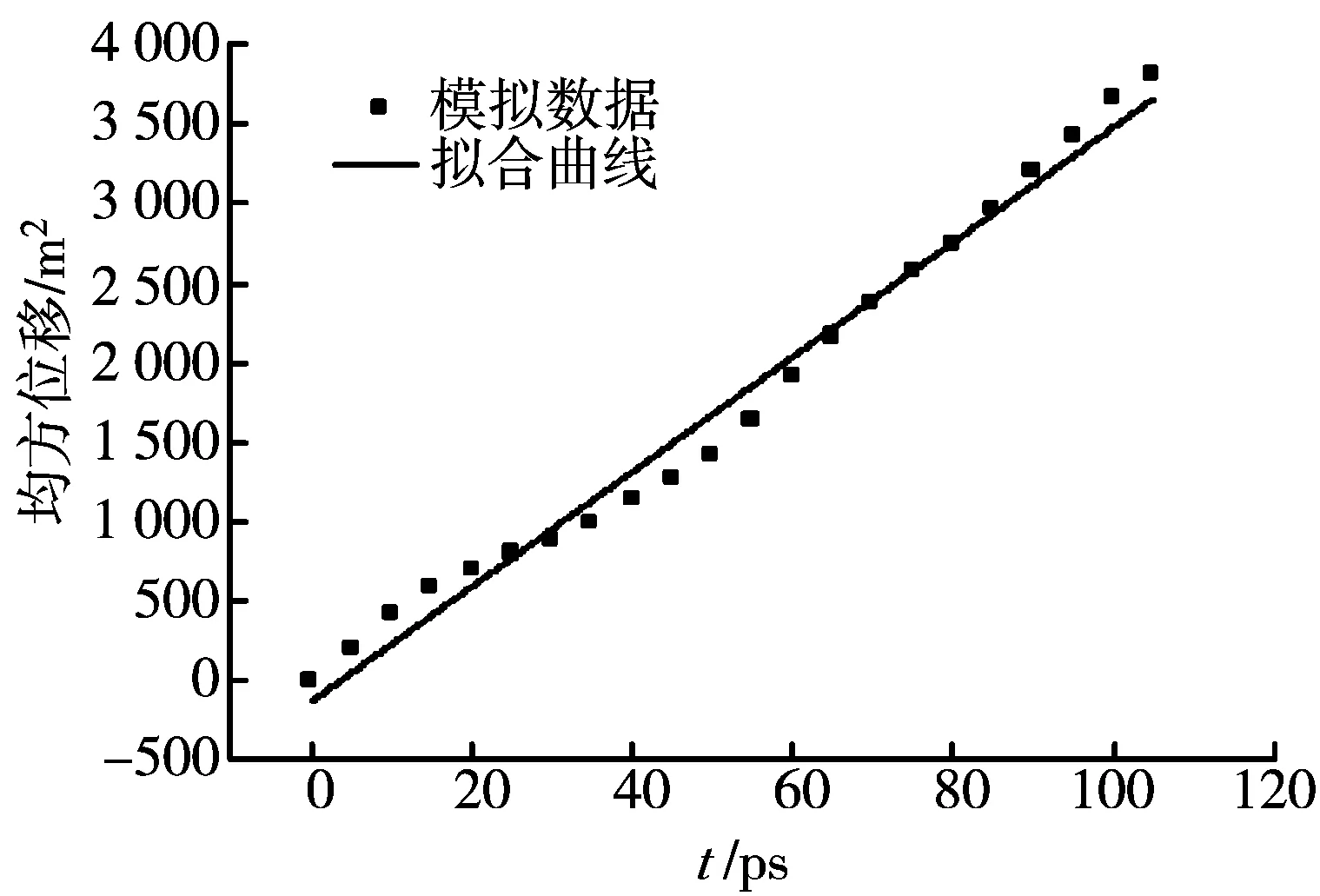
图8 均方位移与时间的拟合曲线

2.2.2 压力对该体系无限稀互扩散系数的影响

在T=323 K，二氧化碳分子数为255，乙醇分子数为1的条件下，MD模拟得到的乙醇—超临界二氧化碳无限稀体系的互扩散系数与压力之间的关系曲线，并与文献值[14]进行了比较，如图9所示。与二氧化碳自扩散系数的变化规律相似，随着压力的增大，互扩散系数不断减小，扩散能力变弱；在低压区，互扩散系数随压力的变化很大，在高压区，压力的影响变得很微弱，扩散系数的降低速率变得很小。

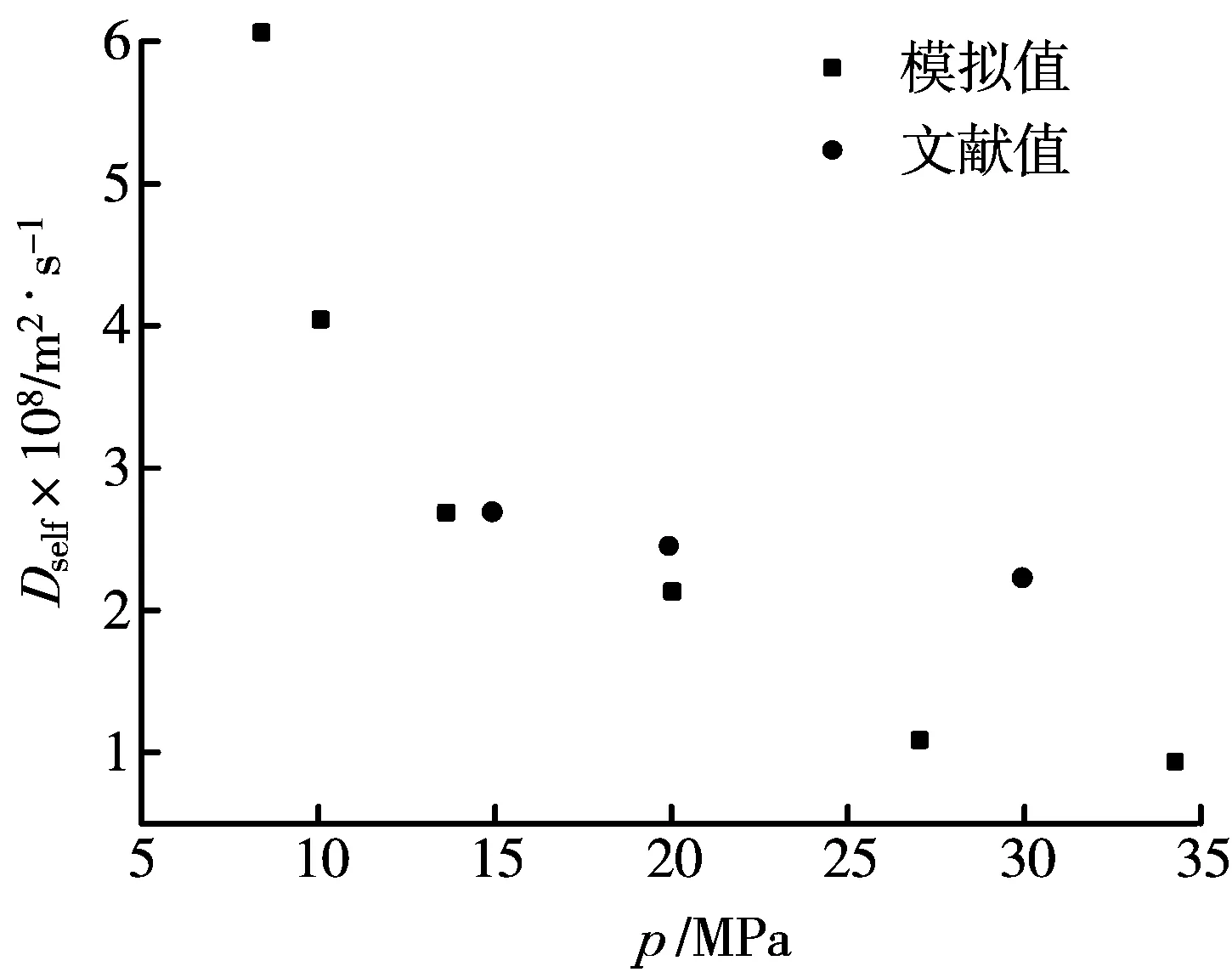
图9 不同压力下互扩散系数的MD模拟结果

2.2.3 温度对该体系无限稀互扩散系数的影响

在二氧化碳分子数为255，乙醇分子数为1，压力p=8 MPa，MD模拟得到的乙醇—超临界二氧化碳无限稀体系的互扩散系数与温度之间的关系曲线，如图10所示。可见，随着温度的升高，互扩散系数增大，扩散能力增强；当温度小于临界温度时，互扩散系数随温度的增大而缓慢地增加，当温度位于临界温度附近时，互扩散系数的增加速率突然增大，曲线有一个明显的转折点。

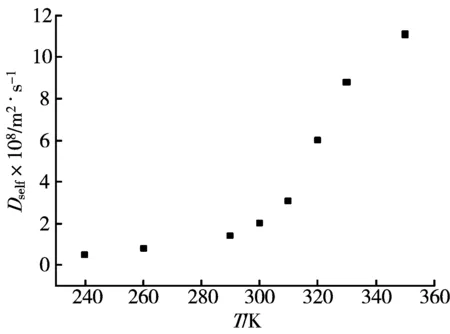
图10 不同温度下互扩散系数的MD模拟结果

3 结论

采用分子动力学模拟方法，考察了温度和压力对超临界二氧化碳自扩散系数和乙醇—二氧化碳无限稀体系互扩散系数的影响。模拟结果表明，超临界二氧化碳的自扩散系数和乙醇—二氧化碳无限稀体系互扩散系数，均随着温度的升高或压力的降低而增大。

[1]张新波.水和二氧化碳体系的分子模拟研究[D].厦门:厦门大学,2007.

[2]Chatzis G,Samios J.Binary mixtures of supercritical carbon dioxide with methanol. a molecular dynamics simulation study[J].Chem Phys Lett,2003,374(1-2):187-193.

[3]Stubbs J M,Siepmann J I.Binary phase behavior and aggregation of dilute methanol in supercritical carbon dioxide:a monte carlo simulation study[J].J Chem Phys,2004,121(3):1525-1534.

[4]俞联梦,刘锦超.二氧化碳—水二元混合流体的分子动力学模拟研究[J].西南民族大学学报：自然科学版,2009,35(6):1248-1254.

[5]Higashi H,Iwai Y,Arai Y.Calculation of self-diffusion and tracer diffusion coefficients near the critical point of carbon dioxide using molecular dynamics simulation[J].Industrial & Engineering Chemistry Research,2000,39(12):4567-4570.

[6]Colina C M,Olivera-Fuentes C G,Siperstein F R,et al.Thermal properties of supercritical carbon dioxide by Monte Carlo simulations[J].Molecular Simulation,2003,29(6-7):405-412.

[7]Zhou J,Lu X,Wang Y,et al.Molecular dynamics investigation on the infinite dilute diffusion coefficients of organic compounds in supercritical carbon dioxide[J].Fluid Phase Equilibria,2000,172(2):279-291.

[8]张 阳.分子模拟在纯超临界流体及其二元混合物体系中的应用[D].北京:清华大学,2005.

[9]李 勇,刘锦超,芦鹏飞,等.从常温常压到超临界乙醇的分子动力学模拟[J].物理学报,2010(7):4880-4887.

[10]Rapaport D C.The art of molecular dynamics simulation[M].Cambridge:Cambridge University Press,1995.

[11]陈正隆,徐为人,汤立达.分子模拟的理论与实践[M].北京:化学工业出版社,2007.

[12]Allen M P,Tildesley D J.Computer simulation of liquids[M].Oxford:Oxford University Press,1989.

[13]Coelho L A F,Oliveira J V,Tavares F W.Dense fluid self-diffusion coefficient calculations using perturbation theory and molecular dynamics[J].Brazilian Journal of Chemical Engineering,1999,16(3):319-329.

[14]何 岩,张敏华,姜浩锡.纯CO2体系扩散性质的分子动力学模拟[J].化学工业与工程,2009,26(1):57-61.

MolecularDynamicsSimulationofDiffusionBehaviorforSupercriticalCarbonDioxide

WANGBao-he1,YANGLiu-wei1,LIQun1,XIALiang-zhi2,WANGGang1

(1.School of Chemical Engineering,Dalian University of Technology,Dalian 116024,China;2.School of Chemical Machinery, Dalian University of Technology,Dalian 116024,China)

Using carbon dioxide EPM2 potential energy model and ethanol TraPPE-UA potential energy model, self-diffusion coefficients of supercritical carbon dioxide and infinite dilute inter-diffusion coefficients of ethanol in supercritical carbon dioxide are investigated by molecular dynamics simulation. The simulation results indicate that the self- diffusion coefficient of supercritical carbon dioxide increases with the temperature increasing or pressure decreasing,as well as the inter-diffusion coefficient of ethanol in supercritical carbon dioxide system.

molecular dynamics;supercritical carbon dioxide;diffusion coefficient;simulation

2014-06-18

王宝和(1959-)，男，副教授，主要从事不同形貌微纳结构的制备、干燥及分子动力学模拟研究，电话：(0411)84986167，E-mail：wbaohe@163.com。

O561

A

1003-3467(2014)08-0031-05