考虑横法向热应变的C0型Reddy层合梁理论
2014-08-29范晓燕
吴 振,范晓燕
(1.沈阳航空航天大学 航空航天工程学部(院),沈阳 110136; 2.辽宁省飞行器复合材料结构分析与仿真重点实验室,沈阳 110136)
考虑横法向热应变的C0型Reddy层合梁理论
吴 振1,2,范晓燕1
(1.沈阳航空航天大学 航空航天工程学部(院),沈阳 110136; 2.辽宁省飞行器复合材料结构分析与仿真重点实验室,沈阳 110136)
考虑横法向热变形和自由表面条件,发展了C0型Reddy层合梁理论。考虑了横法向热应变,发展的C0型Reddy层合梁理论没有增加额外位移变量。发展模型的位移场不含有横向位移一阶导数,方便构造多节点高阶单元。基于虚位移原理,推导出复合材料层合梁的平衡方程并分析简支复合材料层合/夹层梁热膨胀问题。数值结果表明,建立的模型能准确分析复合材料层合/夹层梁热膨胀问题。然而,忽略横法向热应变的理论误差较大。
C0型Reddy层合梁理论;热膨胀;层合/夹层梁;解析解;热应力
由于其具有高强度和低密度、抗疲劳和耐腐蚀等优良特性,复合材料层合结构广泛应用于先进的飞行器和航空航天结构中。复合材料层合结构通常处于热环境状态,这使得复合材料构件不仅受力载荷作用,还受温度载荷作用。由于温度变化和各层的热膨胀系数不协调,复合材料层合结构会出现较大热变形和热应力,从而可能导致结构破坏失效。因此,复合材料层合结构的结构设计中必须考虑温度变化引起的热应力。
通过使用横向剪切应力自由表面条件,Reddy[1]发展了三阶理论,即Reddy理论。Reddy理论不需使用剪切修正系数,横向剪应力沿板厚度方向呈抛物线分布。Khdeir和Reddy[2]研究了正交铺设复合材料矩形层合板的热弹性响应。基于Reddy理论,Shahrokh 等[3]提出了圆形/环形板压电层自由振动的精确解。陈万吉等[4]建立了基于新修正偶应力理论的复合材料Reddy板理论模型。基于Reddy理论各国学者正开展大量研究及应用[5]。由于Reddy理论有效且简单,Reddy理论广泛应用于复合材料层合结构中。然而,Reddy理论位移场含有横向位移一阶导数,难以构造多节点高阶单元。
为了解决Reddy理论难以构造多节点高阶协调单元问题,Bhar等[6]发展了C0型Reddy理论,并分析了复合材料层合/夹层结构的弯曲问题。此理论位移场不含有横向位移一阶导数,构造有限元时避免使用C1型插值函数,便于构造多节点高阶协调单元。然而,C0型Reddy理论[6]忽略了横法向热应变,以至于不能准确分析复合材料层合结构的热膨胀问题。为了推广C0型Reddy理论[6]分析复合材料层合/夹层结构热膨胀问题,本文建立了考虑横法向热应变的C0型Reddy层合梁理论模型。由于考虑了横法向热应变,本文建议的理论模型能准确分析复合材料层合/夹层梁热膨胀问题,而且不增加额外位移变量。如果不考虑温度载荷,此理论能自动退化为C0型Reddy层合梁理论[6]。数值结果表明:对于复合材料层合/夹层梁热膨胀问题,本文建议的模型精度高于C0型Reddy层合梁理论[6]。
1 理论公式
为了考虑横法向应变,本文将温度变化引起的横法向热应变引入到横向位移场。由温度变化引起的横法向热应变可写为[7]:
(1)
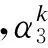
ΔT(x,z)=f(z)T(x)
其中,f(z)为沿厚度方向分布温度构形,T(x)为温度面内分布函数。
沿厚度方向积分方程(1),可得到温度变化产生的横法向热变形:
(2)
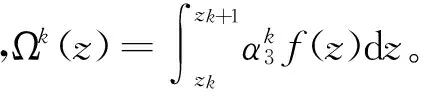
1.1 三阶理论(TOT)
使用泰勒级数展开,面内位移沿厚度方向取三次多项式,而横向位移沿厚度方向假定为常数。则三阶理论(TOT)的位移场为[8]:
u=u0+zu1+z2u2+z3u3
w=w0
(3)
1.2 Reddy层合梁理论(RT)
基于三阶理论(TOT),使用横向剪切自由表面条件,可获得Reddy层合梁理论[1]:
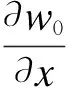
w=w0
(4)
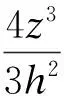
1.3 C0型Reddy层合梁理论(RT-C0)[6]
基于三阶理论(TOT),使用横向剪切自由表面条件消去横向位移的一阶导数获得C0型Reddy层合梁理论的位移场:
u=u0+Ψ1u1+Ψ2u3
w=w0
(5)
其中,Ψ1=z,Ψ2=z2。
1.4 考虑横法向热应变的C0型Reddy层合梁理论
为了分析复合材料层合/夹层梁的热膨胀问题,通过将横法向热应变引入三阶理论(TOT)的横向位移中,考虑横法向热应变的C0型Reddy层合梁理论初始位移场可写为:
u=u0+zu1+z2u2+z3u3
横向剪切应变表达式为:
(6)
通过使用横向剪切应变自由表面条件,消去横向位移一阶导数,考虑横法向热应变的C0型Reddy层合梁理论公式为:
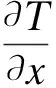
(7)
其中,
公式(7)表明,如果不考虑温度载荷,本文发展的模型自动退化为不考虑横法向应变的C0型Reddy理论[6]。根据位移-应变关系,可得到考虑横法向热应变的C0型Reddy层合梁理论的应变:
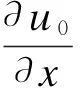
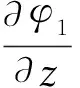
(8)
公式(8)表明,温度项对面内应变和横向剪切应变均有影响,因此C0型Reddy层合梁理论分析复合材料层合/夹层梁的热膨胀问题精度较高。
1.5 考虑横法向热应变的C0型Reddy层合梁理论的解析解
考虑横向剪切变形的热弹性本构关系可表示为:
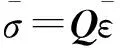
(9)
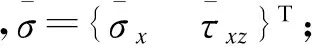
αx表示为沿x轴方向的热膨胀系数,ΔT表示温度变化,Q为偏轴刚度系数矩阵,
其中m=cosφk,n=sinφk,(φk为铺设角)
使用虚位移原理可得到平衡方程。虚功方程可写成:
δU-δW=0
(10)
其中:δU为变形所产生的变形能,δW为外力所做的虚功。
(11)
其中,Px和Pz分别为作用在x和z方向上的外载荷,对于只有热载荷作用下的复合材料层合结构,Px=Pz=0,因此δW=0,从而δU=0。
把公式(7)代入几何方程,然后代入公式(11),并使用分步积分,可得到平衡方程为:
(12)
为检验本文发展的考虑横法向热应变的C0型Reddy层合梁理论的性能,将研究在热载荷作用下的简支梁,其边界条件为[9]:
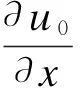
(13)
满足边界条件的未知位移变量可假设如下形式:
(14)
其中,α=mπ/l,(位移模数m=1,2,3,…,∞)
(15)
其中,
通过求解方程(15)得到u0m,u1m,u3m,w0m。
面内位移和面内应力可分别表示为:
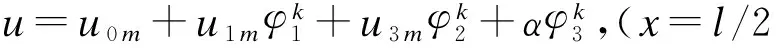
(16)
x=l/2
由于考虑横法向热应变的C0型Reddy层合梁理论为单层理论,没有考虑层间应力连续条件。因此,不能直接应用本构方程计算层间应力。为了获得准确横向剪切应力,三维平衡方程方法将被使用。后处理得到的横向剪切应力可表示为:
(17)
2 算例与分析
为验证考虑横法向热应变的C0型Reddy层合梁理论性能,将研究两边简支复合材料层合/夹层梁的热膨胀问题。梁的长度为l,厚度为h。图1给出受热载荷作用下的简支梁。
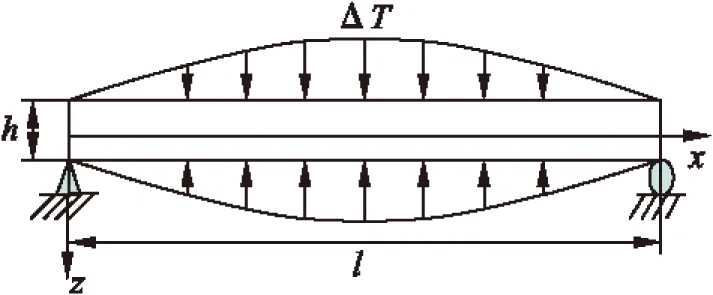
图1 简支梁的受力示意图
2.1 复合材料层合梁的热膨胀问题
在温度场函数ΔT=T0sin(πx/l)的影响下,分析两边简支三层[0°/90°/0°]复合材料层合梁的热膨胀问题。材料常数[10]:EL=181 GPa,ET=10.3 GPa,GLT=7.17 GPa,GTT=2.87 GPa,vLT=0.28,vTT=0.33,αL=0.02×10-6/K,αT=22.5×10-6/K;其中L表示纤维方向,T表示垂直纤维方向。
图2给出对称三层梁[0°/90°/0°]面内应力沿厚度方向分布。结果表明,考虑横法向热应变的C0型Reddy层合梁理论的计算结果与解析解[11]基本一致。然而,忽略横法向热应变的Reddy理论(RT)和C0型Reddy理论(RT-C0)计算的结果精度较低。图3给出了基于不同理论模型
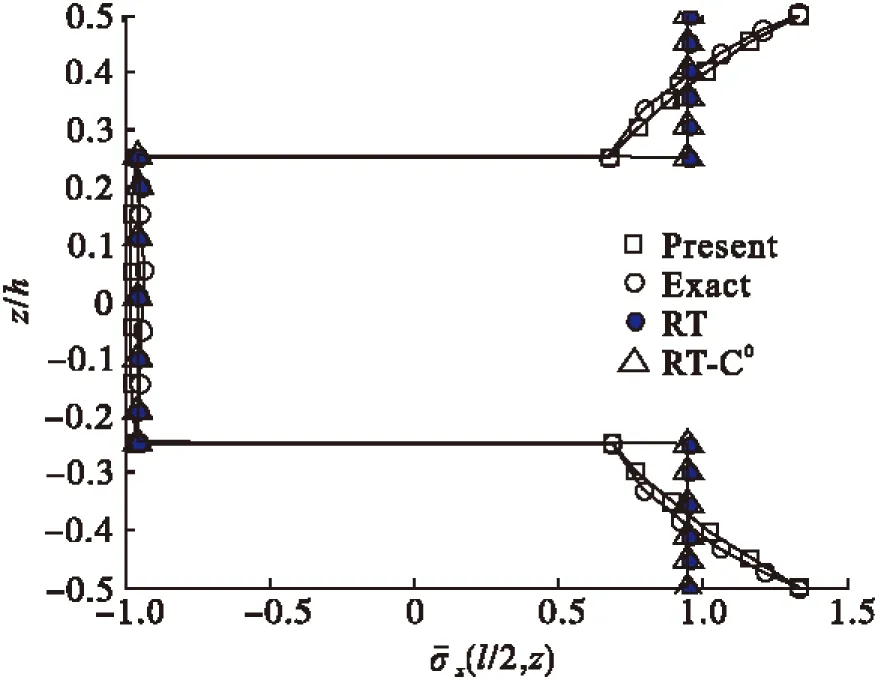
图2 沿厚度方向分布面内应力(l/h=5)
计算的横向剪切应力比较,数值结果表明三种理论计算横向剪切应力精度相当。
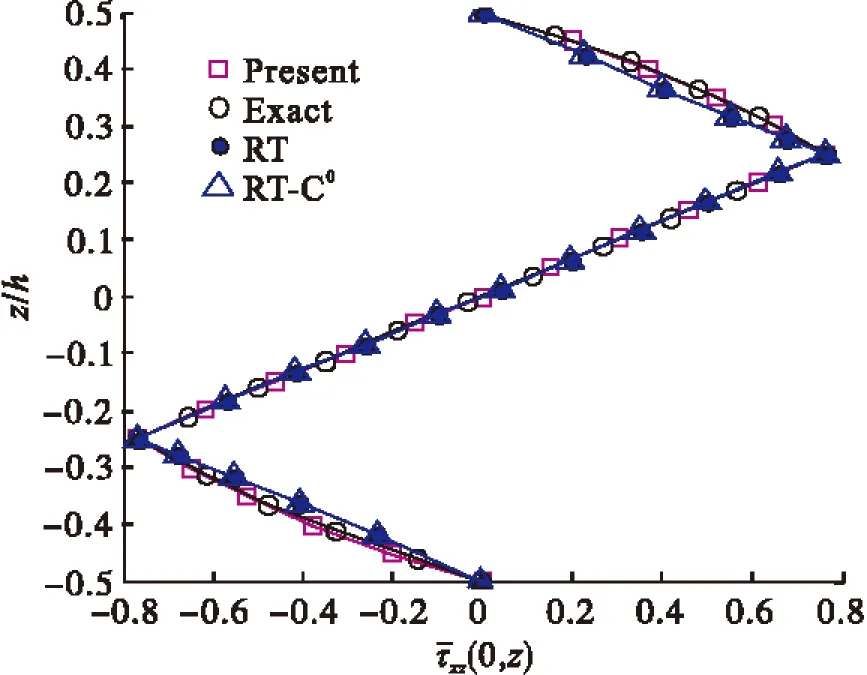
图3 沿厚度方向分布横向剪切应力(l/h=5)
2.2 复合材料夹层梁热膨胀问题
在热载荷ΔT=T0sin(πx/l)作用下复合材料夹层梁热膨胀问题。材料常数[11]:表面层(h/10×2):EL=E0,ET=0.04E0,GLT=0.008E0,GTT=0.02E0,vLT=0.25,E0=144.8 GPa,αL=0.139×10-6/K,αT=9×10-6/K;
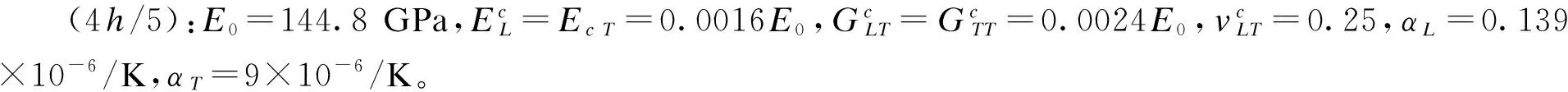
位移和应力进行无量纲化:
此例题研究复合材料夹层梁[0°/core/0°]热膨胀问题,图4-6分别是夹层梁面内位移,面内应力和横向剪切应力沿厚度方向的分布图,结果表明考虑横法向热应变的C0型Reddy层合梁理论计算结果与解析解[11]符合较好。而Reddy理论(RT)和C0型Reddy理论(RT-C0)计算的结果精度较低。对于复合材料夹层梁的热膨胀问题,不能忽略横法向热应变。

图4 沿厚度方向分布面内位移(l/h=5)
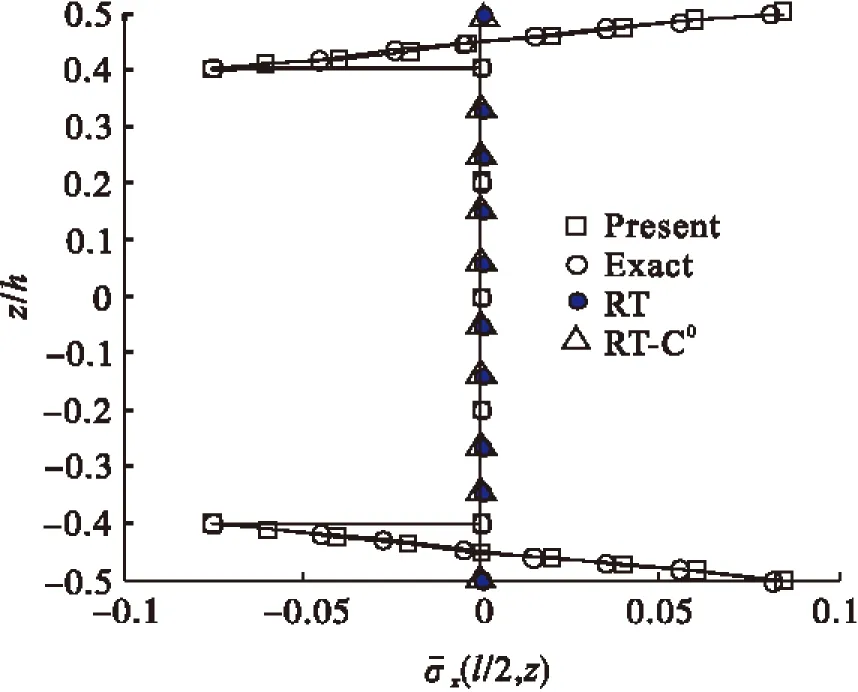
图5 沿厚度方向分布面内应力(l/h=5)
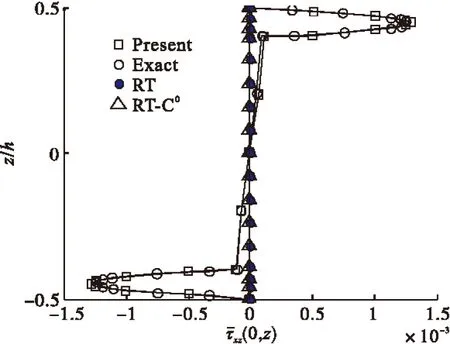
图6 沿厚度方向分布横向剪切应力(l/h=5)
3 结论
为推广C0型Reddy层合梁理论分析复合材料层合结构的热膨胀问题,本文发展了考虑横法向热应变的C0型Reddy层合梁理论。基于虚位移原理,本文推导了复合材料层合梁平衡方程,并给出了简支梁热膨胀问题的解析解。通过分析复合材料层合/夹层梁热膨胀问题,可得出如下结论:
(1)由于忽略横法向热应变,Reddy理论(RT)和C0型Reddy理论(RT-C0)不能准确计算在温度载荷作用下复合材料层合梁的面内应力,不能准确计算夹层梁面内位移,面内应力和横向剪切应力。
(2)考虑横法向热应变并满足横向剪切应力自由表面条件,本文考虑横法向热应变的C0型Reddy层合梁理论能准确分析复合材料层合/夹层梁的热膨胀问题。发展的模型与C0型Reddy层合梁理论位移变量个数同样。
[1]Reddy J N.A simple higher-order theory for laminated composite plates[J].J Appl Mech,1984(51):745-752.
[2]Reddy J N.Analysis of functionally graded plates[J].Int J Numer Methods Eng,2000(47):663-684.
[3]Shahrokh H H,Eshaghi M,Taher HRD.An exact analytical solution for freely vibrating piezoelectric coupled circular/annular thick plates using Reddy plate theory[J].Compos Struct,2010(92):1333-1351.
[4]Chen W J,Ma X,Li L.A model of composite laminated Reddy plate based on new modified couple stress theory[J].Compos Struct,2012(94):2143-2156.
[5]Xiang S,Jiang S X.A nth-order meshless generalization of Reddy′s third-order shear deformation theory for the free vibration on laminated composite plates[J].Compos Struct,2011(93):299-307.
[6]Asadi E,Fariborz S J.Free vibration of composite plates with mixed boundary conditions based on higher-order shear deformation theory[J].Arch Appl Mech,2012(82):755-766.
[7]Talabi M R,Saidi A R.An explicit exact analytical approach for free vibration of circular/annular functionally graded plates bonded to piezoelectric actuator/ sensor layers based on Reddy′s plate theory[J].Appl Math Model,2013(37):7664-7684.
[8]Mendonca P T R,Barcellos C S,Torres DAF.Robust Ck/C0generalized FEM approximations for higher-order conformity requirements:Application to Reddy′s HSDT model for anisotropic laminated plates thoery[J].Compos Struct,2013(96):332-345.
[9]Dong L,Hao Y X,Wang J H,Yang L,Nonlinear vibration of functionally graded material cylindrical shell based on Reddy′s third-order plates and shells thoery[J].Advanc Mater Resear,2013(625):18-24.
[10]Bhar A,Satsangi S K.Accurate transverse stress evaluation in composite/sandwich thick 51:using a C0HSDT and a novel post-processing technique[J].Eur J Mech A/Solids,2011(30):46-53.
[11]Wu Zhen,S H Lo,K Y Sze.Influence of transverse normal strain and temperature profile on thermo-elasticity of sandwiches[J].J Thermal Stresses,2013(36):19-36.
[12]Kant T,Swaminathan K.Analytical solutions for the static analysis of laminated composite and sandwich plates based on a higher order refined theory[J].Compos Struct,2002(56):329-344.
[13]Wu Z,Y K Cheung,S H Lo,Chen W J.On the thermal expansion effects in the transverse direction of laminated composite plates by means of a global-local higher-order model[J].Int J Mech Sci,2010(52):970-981.
[14]Kapuria S,Dumir P C,Ahmed A.An efficient higher order zigzag theory for composite and sandwich beams subjected to thermal loading[J].Int J Solids Struct,2003,40(24):6613-6631.
[15]Matsunaga H.Interlaminar stress analysis of laminated composite and sandwich circular arches subjected to thermal/mechanical loading[J].Compos Struct,2003(60):345-358.
(责任编辑:宋丽萍 英文审校:刘红江)
C0-typeReddy′sbeamtheoryconsideringtransversenormalthermalstrain
WU Zhen1,2,FAN Xiao-yan1
(1.Foculty of Aerospace Engineering,Shenyang erospace University,Shenyang 110136,China;2.Key Laboratory of Liaoning Province for Composite Structural Analysis of Aerocraft and Simulation,Shenyang 110136,China)
By considering the transverse normal thermal deformation and the free surface conditions,a C0-type Reddy′s theory for laminated composite beams is proposed.Although transverse normal strain is taken into account,the number of the unknown offset variables in the proposed model is not increased.Moreover,the first derivatives of transverse displacement are taken out from the in-plane displacement fields,so that it is convenient to construct higher-order elements.Based on the principle of virtual displacement,the equations of equilibrium for laminated composite beams are presented,and the thermal expansion problems of laminated composite and sandwich beams are studied.Numerical results show that C0-type Reddy′s beam theory considering transverse normal thermal strain can accurately analyze the thermal expansion problems of laminated composite structures.However,the models neglecting transverse normal strain are less accurate.
C0-type Reddy′s beam theory;thermal expansion;laminated composite and sandwich beams;analytical solution;thermal stress
2014-01-03
国家自然科学基金(项目编号:11272217);辽宁高校优秀人才支持项目(项目编号:LR201033)
吴振(1977-),男,黑龙江佳木斯人,教授,博士生导师,主要研究方向:复合材料力学研究,E-mail:wuzhenhk@163.com。
2095-1248(2014)03-0009-05
TB12
A
10.3969/j.issn.2095-1248.2014.03.002
