基于有限元法对裂纹尖端应力强度因子的计算

杨 巍，张 宁，许 良,3

(1.中航工业沈阳飞机工业(集团)有限公司 制造工程部，沈阳 110136； 2.沈阳航空航天大学 机电工程学院，沈阳 110136；3.沈阳航空航天大学 航空制造工艺数字化国防重点实验室，沈阳 110136)

基于有限元法对裂纹尖端应力强度因子的计算

杨 巍1，张 宁2，许 良2,3

(1.中航工业沈阳飞机工业(集团)有限公司 制造工程部，沈阳 110136； 2.沈阳航空航天大学 机电工程学院，沈阳 110136；3.沈阳航空航天大学 航空制造工艺数字化国防重点实验室，沈阳 110136)

基于ANSYS有限元软件通过相互作用积分法建立了求解三维穿透裂纹应力强度因子的有限元模型，将有限元法和解析法求得的应力强度因子进行比较验证了模型的准确性。研究了载荷、裂纹长度、试样宽度、厚度对裂纹尖端应力强度因子的影响，在对比结果的基础上分析了裂纹尖端应力强度因子的三维效应。结果表明：在不同条件下有限元模型都可以很好的模拟出应力强度因子的值，二维状态时应力强度因子的分布规律与三维状态时的分布规律有较大差异，出于安全的考虑不应忽略应力强度因子的三维效应，对三维应力强度因子的有限元求解有一定的指导意义。

相互作用积分方法；三维穿透裂纹；应力强度因子；ANSYS

断裂是工程构件最危险的一种失效方式，尤其是脆性断裂，它是突然发生破坏，断裂前没有明显的征兆，这就常常引起灾难性的事故。大量断裂事故分析中发现，断裂皆与结构中存在缺陷或裂纹有关。由缺陷或裂纹所引起的机械、结构的断裂失效,是工程中最重要、最常见的失效模式[1]。传统强度理论是建立在假设材料无缺陷的基础上的,但工程实际中很多按传统强度理论设计的结构由于裂纹的产生和扩展,出现大量断裂失效。为保证含裂纹构件的安全性和可靠性,必须预测裂纹的扩展速率和构件的断裂强度,在断裂力学的工程应用中,应力强度因子K是判断含裂纹结构的断裂和计算裂纹扩展速率的重要参数。应力强度因子的计算方法有解析法、有限元法、边界元法、权函数法等[2]。解析法可以得到理论上的精确解,但不适应工程实际当中复杂的条件(如结构形状、载荷情况、裂纹形式等)。而有限元法具有强大的建模能力和可以充分利用计算机的计算能力,可以解决复杂几何状况,各种边界条件下的平面和空间问题以及各向异性、热应力和非线性问题,并能获得较高的精度,已成为确定应力强度因子的最有效方法。

本文以平板类穿透性裂纹为研究对象，利用有限元软件ANSYS建立了含裂纹平板的有限元模型，采用相互作用积分法计算了裂纹尖端的应力强度因子KI，与解析法的计算结果进行了对比，并且研究了载荷、裂纹长度、试样宽度、厚度对裂纹尖端应力强度因子的影响。

1 相互作用积分法

1.1 相互作用积分的定义

如式(1)所示，RICE提出了J积分[3]，

(1)

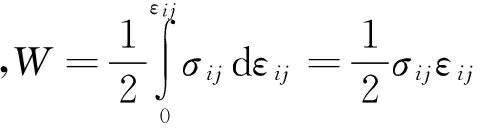
(2)

整理得到：

J(1+2)=J(1)+J(2)+M(1,2)

(3)

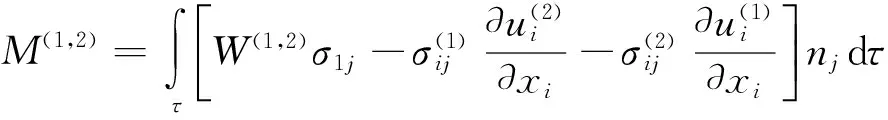
(4)

(5)

1.2 应力强度因子的提取

对于线弹性情况，J积分、应变能释放率和应力强度因子存在如下关系[4]：

(6)

其中,E和υ为裂纹尖端处的弹性模量和泊松比。类似地，相互作用积分

(7)

2 应力强度因子的有限元计算

在ANSYS中求解断裂力学问题,首先要进行弹性分析或弹塑性静力分析,然后再用特殊的后处理命令，或宏命令计算所需的断裂参数。

2.1 有限元模型的建立

本文模型的建立是基于含中心穿透裂纹平板试样(M(T)试样)。如图1所示，宽度为2W，厚度为2B，穿透裂纹长度为2a。由于裂纹尖端存在较高的应力梯度且尖端处具有奇异性,Barsoum、Henshell和Shaw[5]分别发现通过把裂纹尖端附近二阶单元的中间节点沿裂纹尖端方向移至靠近裂尖1/4分点处(如图2中B点)就可以使裂尖附近应力场达到奇异性。因此，裂纹尖端附近采用奇异单元划分网格，远离裂纹的余下部分采用常规单元进行划分[6]。图3为有限元模型的网格划分，尖端网格尺寸为a/12，围绕裂纹尖端一圈的网格数量为15，每层网格尺寸的增长比例为1∶1。建模过程中平面单元采用plane183，实体单元采用solid186，沿板厚度方向单元层数取5。裂纹所在延长线上分别由裂纹尖端至两端网格宽度逐渐增大，比率为10∶1。模型的底端固定，板远端作用有均布应力，弹性模量和泊松比分别为E=195 GPa和μ=0.3。通过ANSYS求解出裂纹尖端的应力、应变和位移场(图4为等效应力云图)并将其与相互作用积分的公式结合，再通过相互作用积分与应力强度因子的关系导出KI值。

2.2 有限元模型的验证

GB/T6398-2000中给出的求解断裂力学中有限大平板的应力强度因子公式为：

(8)

本文中的解析解均按照式(8)计算得出。

图1 中心穿透裂纹平板试样示意图

图2 裂纹尖端奇异单元

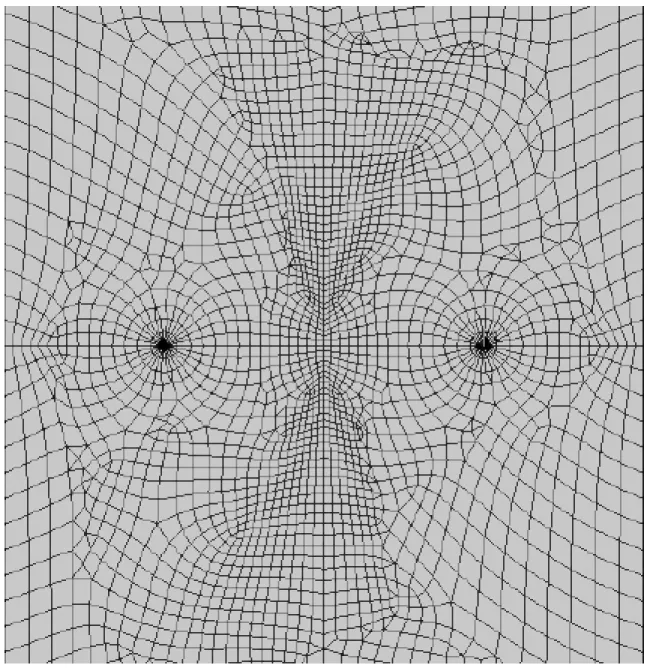
图3 模型的网格划分

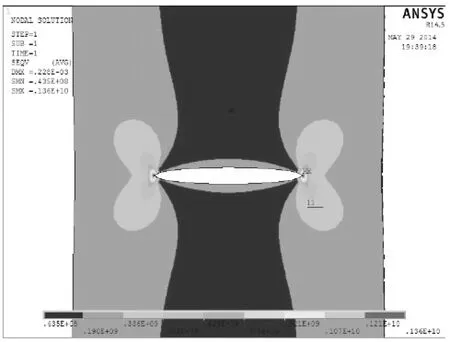
图4 裂纹尖端等效应力云图

表1算例参数

参数符号2W/mmt/mmH/mma/mmE/GPaμσ/MPa参数值502200101950.3200

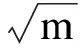
3 应力强度因子的有限元分析

随着施加载荷、裂纹长度和试样尺寸的改变，应力强度因子的求解结果也会随之改变，为了研究这些因素对有限元方法计算KI值的影响，本文对比了不同条件下的有限元法和解析法的计算结果。

表2至表4为不同条件下应力强度因子计算结果对比，图5为变化趋势图。

3.1 二维应力强度因子的影响因素

由表2和图5a所示，有限元法和解析法在不同载荷的情况下具有相同的变化趋势，均随着载荷的增加呈线性增长。且各应力水平下的相对误差均低于2%。模型在相同应力水平σ=200 MPa的前提下不同裂纹长度所对应的应力强度因子KI如表3和图5(b)所示。由表3可知不同裂纹长度下KI值的相对误差低于2.5%，说明该模型可以很好的仿真出不同裂纹长度下的KI值；在相同的裂纹长度增幅下所求得的KI值前后相差量逐渐增大即随着裂纹长度的增加应力强度因子KI的增长速率变快。当只改变平板宽度W，取W分别为50 mm、75 mm、100 mm、130 mm、170 mm，即a/W=0.4、0.267、0.2、0.154、0.118，

表2 不同载荷时KI计算结果

表3 不同裂纹长度时KI计算结果

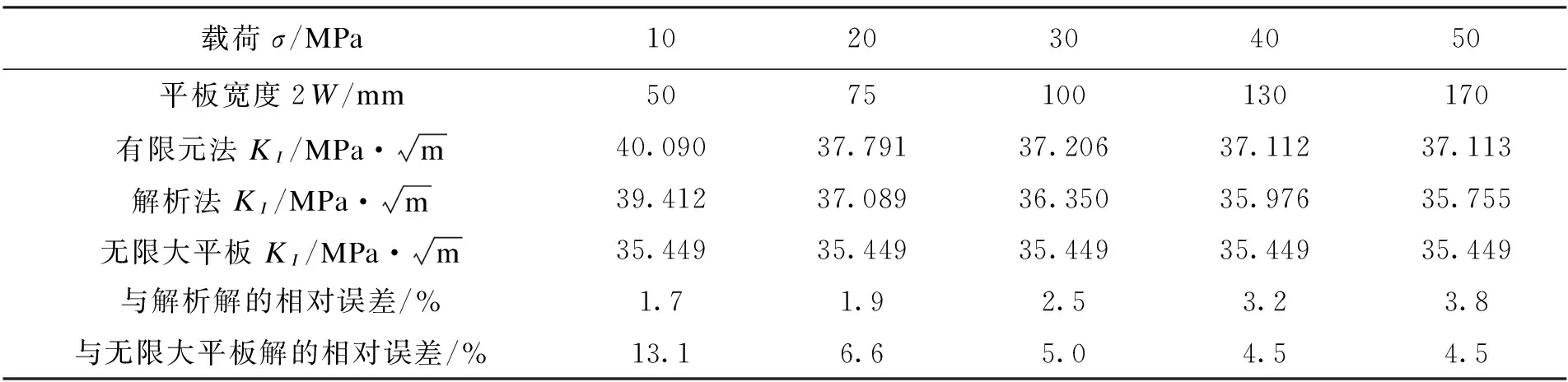
表4 不同平板宽度时KI计算结果

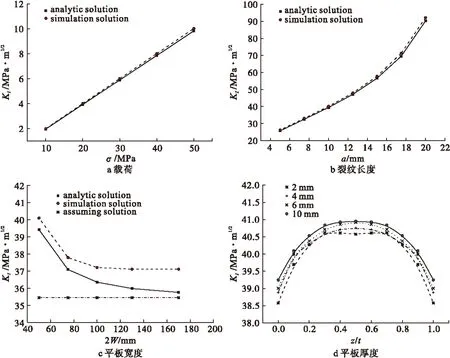
图5 不同条件下应力强度因子KI曲线的比较

由表4和图5c可知，随着a/W的减小应力强度因子KI值也在减小，当a/W<0.2时KI值逐渐趋于一定值，符合断裂力学中“无限大”平板的假设。

3.2 三维应力强度因子的影响因素

随着断裂力学学科的发展，许多研究者不满足于将裂尖附近的三维问题等效为二维问题来看待，进而开展了许多关于三维应力强度因子的研究[7-14]，这些研究都表明裂纹尖端的应力场有着强烈的三维效应。图5d为裂纹长度a/W=0.4不同厚度(t=2,4,6,10 mm)含有中心穿透裂纹板应力强度因子沿厚度变化规律。显然，应力强度因子沿厚度的方向分布是不均匀的，但从中不难发现一些规律：无论式样的厚度如何变化，在裂纹前缘的中心处(z/t=0.5)附近应力强度因子值最大，从中心分别向两表面处(z/t=0,1)延伸应力强度因子值逐渐减小且减小幅度越来越大，在沿试样厚度方向的两表面处达到最小值；从整体上看随着试样厚度的增加裂纹前缘各处的应力强度因子的值均有所增大。

相互作用积分类似于J积分都是基于能量平衡理论产生的方法。金属材料抵抗裂纹扩展的能力分为两部分，分别是形成裂纹新表面所需的表面能和裂纹扩展所需的塑性变形能。试样的中心面由于受厚度方向的约束较大，所以塑性区尺寸较表面处的塑性区要小即需要克服的塑性变形能减少，而随着试样厚度的增加厚度方向的约束愈来愈大，导致在其他条件相同的情况下试样越厚其塑性区尺寸越小所需克服的塑性变形能越小[15]，这也与图4d中不同厚度含有中心穿透裂纹板应力强度因子沿厚度变化规律相符合。

由以上分析可以看出，二维状态时应力强度因子的分布规律与三维状态时的分布规律有较大差异，在工程应用中人们通常会忽略这些差异从而使构件裂纹扩展速率的计算以及剩余寿命的评估不够准确，容易留下隐患。

4 结论

(1)基于相互作用积分法建立了求解应力强度因子的三维有限元模型，并将有限元数值解与解析解进行了对比误差仅为1.7%，证明了有限元模型求解的准确性。

(2)分别通过有限元法与解析法计算了不同载荷、裂纹长度、试样宽度情况下的应力强度因子，结果表明有限元法可以很好的模拟不同条件下的应力强度因子，且当a/W<0.2时有限元求得的解趋于定值，此时的平板可以近似看作“无限大”板。

(3)根据所建立的模型对不同厚度试样的应力强度因子进行求解，结果表明：应力强度因子沿厚度的分布不是均匀的，有限厚度板材板厚度中心应力强度因子最大且沿厚度方向逐渐减小；在所验证的厚度范围内试样越厚其应力强度因子越大。因此，对有限厚度裂纹问题仅考虑二维状态是不安全的。

[1]陈传尧.疲劳与断裂[M].武汉:华中科技大学出版社，2002：1-14.

[2]程勒.断裂力学[M].北京:科学出版社，2006：8-12.

[3]Rice J R.A path independent integral and the approximate analysis of strain concentration by notches and cracks[J].J.Appl.Mech,1968(35)：379-386.

[4]于红军，果立成，国峰楠,等.材料属性连续性对边裂纹应力强度因子的影响[J].哈尔滨工业大学学报，2011,43(S1)：16-20.

[5]Fehl B D，Truman K Z.An Evaluation of Fracture Mechanics Quarter Point Displacement Techniques Used for Computing Stress Intensity Factors[J].Engineering Structures，1999，21(3)：406-415.

[6]王峰.三维应力强度因子分析及干涉预应力影响研究[D].西安：西北工业大学，2007：25-30.

[7]汤英，张晓晶，吴学仁.单边缺口拉伸试样喷丸强化残余应力及其三维应力强度因子分析[J].航空学报，2011，33(7)：1265-1274.

[8]谢伟，黄其青.塑性区阻止效应对三维裂纹应力强度因子的影响研究[J].西北工业大学学报，2005，23(5)：585-588.

[9]杨政，霍春勇,郭万林,等.有限厚度板穿透裂纹前缘附近三维弹性应力场分析[J].应用力学学报，2003，20(3)：74-78.

[10]何宇廷，傅祥炯.铝合金 CCT 试样裂纹扩展三维尺寸效应金相分析[J].空军工程大学学报，2002，3(2)：5-8.

[11]Guo W.Three-dimensional analyses of plastic constraint for through-thickness cracked bodies[J].Eng Fract Mech，1999，62：383-407.

[12]Sternberg E，Sadowsky M A.Three-dimensional solution for the stress concentration around a circular hole in a plate of arbitrary thickness[J].J Appl Mech，1949，16：27-36.

[13]Hartranft R J，Sih G C.An approximate three-dimensional theory of plates with application to crack problems[J].Int J Eng Sci，1970(87)：11-29.

[14]Guo W.Elastoplastic three dimensional crack border field-I singular structure of the field[J].Eng Fract Mech，1993(46)：93-104.

[15]张诗捷,朱亦钢,黄新跃,等.试件厚度对铝合金疲劳裂纹扩展的影响[J].航空学报，1994，6(6)：757-760.

(责任编辑：宋丽萍 英文审校：刘红江)

CalculationofstressintensityfactorsofcracktipsbasedonFEM

YANG Wei1,ZHANG Ning2,XU Liang2,3

(1.The Manufacturing Engineering Department,Aviation Industry Corporation of China,Shenyang 110136,China; 2.College of Mechanical and Electrical Engineering,Shenyang Aerospace University,Shenyang 110136,China; 3.Key Laboratory of Fundamental Science for National Defense of Aeronautical Digital Manufacturing Process,Shenyang 110136,China)

Based on ANSYS software,the calculation model of stress intensity factors(SIF)was built utilizing the interaction integral method to predict the SIF for 3D straight through cracks.The theoretical calculation results are used to compare with the results calculated by using the FEM method.The results of the comparison testify the accuracy of the model.The influences of load,crack length,width and thickness on crack-tip stress intensity factor are studied.Based on the comparison,the 3D effects of the crack tip stress factors are analyzed.According to the results,the calculation model of SIF can simulate the value of SIF accurately in different situations.There are huge differences between the 2D and the 3D on the distribution of SIF.The method is conductive for calculating crack-tip stress intensity factor.

interaction integral method;3D straight through crack;SIF;ANSYS

2014-04-11

杨巍(1982-)，男，辽宁沈阳人，工程师，主要研究方向：结构强度及完整性性评定，E-mail:421852615@qq.com。

2095-1248(2014)03-0019-05

O346.1

A

10.3969/j.issn.2095-1248.2014.03.004