基于核主成分分析的发动机性能衰退评估

谭 巍，徐 健，张 睿

(1.中国人民解放军海军航空兵学院 飞行理论系，辽宁 葫芦岛 125001； 2.海军驻沈阳地区发动机专业 军事代表室，沈阳 110031；3.沈阳航空航天大学 机电工程学院，沈阳 110136)

基于核主成分分析的发动机性能衰退评估

谭 巍1，徐 健2，张 睿3

(1.中国人民解放军海军航空兵学院 飞行理论系，辽宁 葫芦岛 125001； 2.海军驻沈阳地区发动机专业 军事代表室，沈阳 110031；3.沈阳航空航天大学 机电工程学院，沈阳 110136)

针对发动机在使用过程中的性能衰退评估问题，提出了一种基于核主成分分析的发动机参数特征提取方法。通过对发动机性能衰退程度的分类，并与传统的主成分分析方法相比，该方法能够较好地解决航空发动机各参数之间存在的非线性问题，能够在保留原始数据主要信息的基础上获得较好的降维效果，在处理小样本非线性参数指标综合和维数压缩处理方面具有一定的推广价值。

性能衰退；状态评估；核主成分分析；主成分分析

发动机性能衰退评估是对其运行状态的模式识别[1]，其实质是利用当前数据和历史数据，获取发动机当前运行状态的信息，识别发动机当前运行状态，为发动机的状态监控和后续的趋势预测打下良好的基础。张亮提出了一种基于粗糙核距离度量的复杂装备健康评估方法，首先用粗糙集进行健康特征的约简和权重系数的确定,以得到优化的联合健康特征向量,然后基于加权核距离度量进行健康状态分类[2]。杨帆针对核主元分析方法只能实现故障诊断,但无法实现故障变量识别的问题,提出一种基于数据重构的核主元分析的故障变量识别方法。采用改进的数据重构方法对参数进行重构,然后利用故障识别指数对监控参数进行故障变量识别[3]。

发动机在运行过程中，由于气流通道污染引起性能衰退，会导致发动机气路部件的特性变化，引起压气机抽气能力、涡轮效率下降。特性参数的变化会导致转速、流量、供油量、温度、压力等气流通道的热力性能参数发生变化[4]。这些监测参数众多，会对后续的模式分析造成维数灾难问题。为解决这一问题，本文将核主成分分析应用到多维数据的约简中，并使用相关数据对约简效果进行了分析，最后通过发动机状态分类结果验证了核主成分分析方法的有效性。

1 基于核主成分分析的数据特征约简

主成分分析[5]是一种常用的特征提取、特征约简方法，它利用特征向量方向上投影的子空间，得到主特征矢量。依据输入变量的线性变换，由输入变量的互相关矩阵的主要特征值大小确定坐标变换和变量压缩，其目的就是在数据空间中找出一组正交矢量，它们最大可能地捕获数据方差，以便将数据从原始的n维空间中映射到这组正交矢量所生成的m维子向量上，完成降维的任务，得到主特征矢量。但是，由于航空发动机结构复杂，工作情况多变，再加以发动机中一些结构的非线性，使得发动机的工作参数具有一定的非线性特征。通过上述基于线性变换的特征选择方法提取的特征可能不再反映这种非线性特征，当数据间存在大量非线性关系时，主成分分析已不能满足需求。为此，Scholkopf等人[6]在研究支持向量机的时候提出了一个新方法，那就是通过核函数方法将原始输入向量映射到高维特征空间，然后在高维空间中对映射数据进行线性PCA计算，实现对数据维数的降低，这种方法称为核主成分分析[7](Kernel Principal Component Analysis，KPCA)。

1.1 核主成分分析的基本原理

核主成分分析是通过使用“核技巧”将线性PCA 拓展为非线性PCA 的一种方法[8-9]。具体推导过程如下:

首先对原始数据中心化，将原始样本集的核矩阵K用K来取代，即

(1)

式中，I表示n×n维的单位矩阵，ln表示n×n维的全1矩阵。

(2)

(3)

将每个样本与式(3)做内积，则有

λ(φ(xk)·▽)=(φ(xk)·C▽)

k=1,2,L,N

(4)

对于特征向量▽来说，可以用φ(xi)的线性组合表示为

(5)

合并式(4)和式(5)得到

(6)

定义一个m×m维的矩阵K，可以得到

Kij=(φ(xi)·φ(xj))

(7)

其中，α=(α1,L,αm)T，通过求解特征方程得到α

mλα=Kα

(8)

进一步得到式(5)，为提取主成分，需要计算φ(x)在特征空间上的投影。

k=1,2,L,p

(9)

1.2 算法求解主要步骤

通过上述分析，可以看出该算法的流程为：

(1)首先对输入样本进行初始化，计算m×m维的核矩阵K={k(xi,xj)}。

(2)中心化核矩阵K，得到核矩阵K。

(3)求出核矩阵K的特征值和特征向量，并归一化特征向量，得到高维空间中的特征向量主成分。

1.3 数据约简判别准则

核主成分方法首先将在原空间中非线性不可分的数据映射到高维特征空间中，然后在该空间中利用线性PCA算法进行特征约简。而Fisher判别函数[11]通过选择使得Fisher准则函数达到极值的向量作为最佳投影方向，从而使得样本在该方向上投影后，达到最大的类间离散度和最小的类内离散度。因此，为了寻求优化数据的约简方法，可以借鉴Fisher判别函数思想。

Fisher判别准则是针对两类数据的情况提出的。设训练样本集Ω中包含n个d维样本{xi,yi},yi∈{1,-1},i=1,2,L,n，其中n1个属于“+1”类的样本记为X1，n2个属于“-1”类的样本记为X2，即

X1={x1i|(x1i,yi)∈Ω,yi=+1}i=1,2,L,n1

(10)

X2={x2i|(x2i,yi)∈Ω,yj=-1}j=1,2,L,n1

(11)

则这两类在特征空间中的均值向量分别为

(12)

(13)

类间距离的平方为

(14)

X1内离散度的平方为

(x1i,x1i)

(15)

同理，有

(16)

样本的类内离散度矩阵Si和总类内离散度矩阵Sw为

(17)

Sw=S1+S2

(18)

样本类间离散度矩阵Sb为

Sb=(m1-m2)(m1-m2)T

(19)

定义类内类间距离为

(20)

根据Fisher准则的判别思想，(m1-m2)越大越好，Sb越小越好。因此，综合来看，数据之间的类内类间距离J(θ)越大，分类效果越好。

2 仿真与分析

2.1 原始数据核主成分的构建

本文选取发动机低压压气机流量、高压压气机流量、高压涡轮效率、低压涡轮效率、低压转子转速、高压转子转速、高压压气机后压力、尾喷口温度共8维数据，均为相对变化量。采用机理分析和发动机数学模型相结合的方法产生数据样本[12-15]，得到46组发动机性能衰退数据，定义绝对值在0～0.2%变化的参数为性能正常的数据(分类记为-1)；否则为性能衰退的数据(分类记为+1)。

采用支持向量机方法对发动机正常数据和性能衰退数据进行分类[16]。在分类之前，为了检验核主成分分析对数据的约简能力，本文还选取了主成分分析方法处理原始数据，以此作为对比。三种形式的数据分别为：原始数据、原始数据利用主成分方法得到的数据、原始数据经核主成分分析得到的数据。其中，原始数据经过主成分分析和核主成分分析后的结果分别见表1和表2。

表1 主成分分析结果

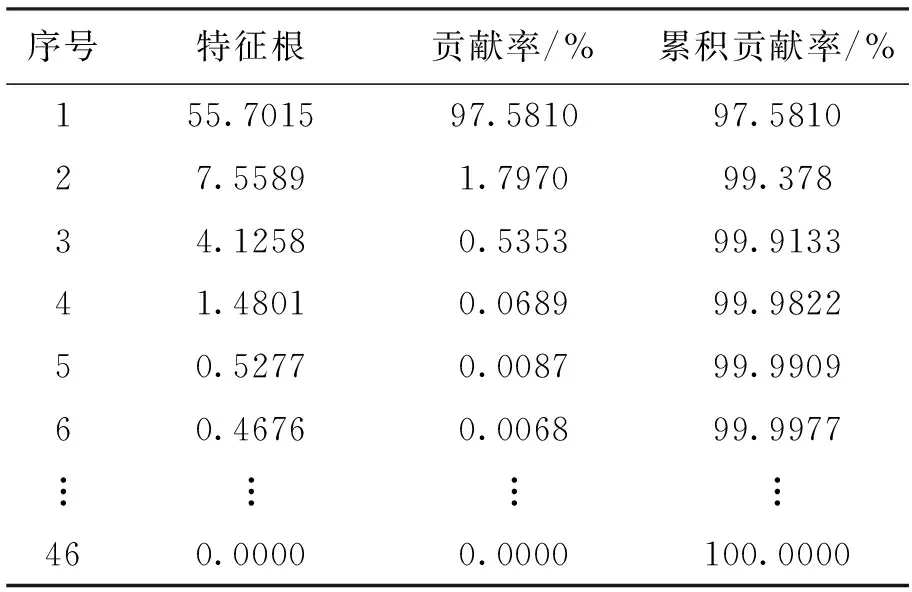
表2 核主成分分析结果

从表1和表2可以看出主成分分析和核主成分分析都可用于样本数据的特征选择，达到降低样本数据维数的目的。但是核主成分分析主元数远多于主成分分析的主元数，核主成分分析有46个主元，而主成分分析只有8个主元，因此核主成分分析主元携带的信息更为全面、丰富；核主成分分析是从46个主元中选取需保留的主元，而主成分分析只是从8个主元中选取需保留的主元，并且按照累积贡献率的大小来看，前3个主成分的累积贡献率已经达到99.9%，因此只需要选择前面3个核主成分就可以达到与主成分分析一样的效果[17]，这样可避免丢失较小的主元中可能包含的重要非线性特征信息，同时还不会带来更多的噪声信息，这说明核主成分分析能够选择更有利于数据分类的特征。

依据判别准则[18-19]，类间距离越大对应分类效果越好。3种数据对应的类内类间距离计算结果见表3。

表3 3种数据形式对应的类内类间距离

从表3可以看出，原始数据形式与主成分分析的方法得到的类内类间距离相同，这是因为主成分分析是对原始数据进行线性变换，并不能改变原始数据的类内类间距离。而核主成分分析是非线性的，它利用核函数对原始数据进行了高维空间的特征映射[20]，本文选择高斯核函数作为核主成分分析的核函数，经计算，核主成分分析数据所对应的类内类间距离最大，因此采用原始数据经核主成分分析方法得到的数据进行分类会取得较好的效果。

2.2 分类结果分析

采用高斯核函数支持向量机方法对3种形式的数据进行分类。取前3个主成分在二维和三维情况进行分类，结果如图1～图6所示。

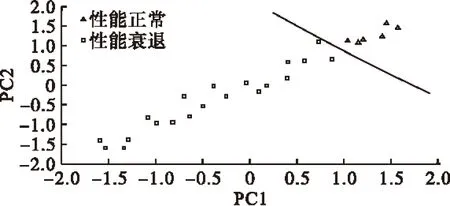
图1 原始数据的二维分类结果

图2 原始数据的三维分类结果

图3 主成分分析数据的二维分类结果

图4 主成分分析数据的三维分类结果

图5 核主成分分析数据的二维分类结果

图6 核主成分分析数据的三维分类结果

图1、图3和图5分别是原始数据、主成分分析数据以及核主成分分析数据的二维分类结果，对于二维分类情况，三种数据形式在二维情况下，利用支持向量机方法都能得到很好的分类。图2、图4和图6分别是原始数据、主成分分析数据以及核主成分分析数据的三维分类结果，从这三幅图中可以看出，三种数据形式在三维分类情况下，原始数据、主成分分析的数据得不到很好的分类，而核主成分分析得到的数据仍能得到很好的分类。究其原因，在二维情况下，两个主成分的线性趋势较强，所以三种数据形式都能得到很好的分类；在三维情况下，三个主成分的线性趋势变弱，非线性趋势增加，虽然采取了主成分分析的方法，但主成分分析是一种线性变换，而性能衰退数据的非线性程度很强，所以对非线性主成分进行分类并不能得到很好的分类结果，图4可以说明这点。而核主成分分析则把低维的非线性不可分关系变成高维的线性可分关系，从图5和图6可以看出，两主成分和三主成分情况都呈线性分布趋势。图6指出对应核主成分分析的情况，性能衰退越严重，主成分参数离最优分界面距离越远，图6三维分类中的主成分参数对应的衰退程度依次增大。

3 结论

针对发动机性能衰退过程中的衰退程度的分类进行了研究，通过核主成分分析方法对发动机状态数据进行了特征约简，并对数据进行了分类，得出如下结论。

(1)相对于原始数据和经主成分分析方法约简后的数据来说，采用核主成分分析方法提取的特征主成分数据在二维和三维情况下都能对发动机的性能衰退状态进行很好的分类。

(2)KPCA方法能较好的解决航空发动机各参数之间存在的非线性问题，能够在保留原始数据主要信息的基础上获得较好的降维效果，具有一定的推广价值。

(3)在对发动机进行性能衰退评估过程中，如何综合发动机的各个性能数据，建立反映发动机性能衰退的综合指标，对于指导发动机工作人员掌握发动机工作状态十分重要，在下一步的工作中要加强对这方面的研究。

[1]Lee J.Measurement of machine performance degradation using a neural network model[J].Computers In Industry,1996,30(3):193-209.

[2]张亮,张凤鸣,杜纯.复杂装备健康状态评估的粗糙核距离度量方法[J].计算机工程与设计,2009,30(18):4269-4271.

[3]杨帆,李应红,石斌.一种基于数据重构的KPCA故障识别方法[J].控制工程,2007,14(7):109-112.

[4]廉筱纯,吴虎.航空发动机原理[M].西安:西北工业大学出版社，2001：101-104.

[5]欧阳成丽.基于主成分分析的航空发动机单元体性能辨识[D].天津：中国民用航空学院，2004:15-16.

[6]Scholkopf B,Smola A,Muller K.Nonlinear component analysis as a kernel eigenvalue problem[J].Neural Computation,1998,10(5):1299-1319.

[7]Cao L J,Chua K S,Chong W K,et al.A comparison of PCA,KPCA and ICA for dimensionality reduction in support vector machine[J].Neurocomputing,2003,55(1-2):321-33.

[8]胡金海,谢寿生,陈卫,等.基于核函数主元分析的航空发动机故障检测方法[J].推进技术，2008,29(1):79-83.

[9]孙丽萍,陈果,陈立波,等.基于KPCA的航空发动机滑油滤磨屑图像识别[J].机械科学与技术,2010,29(6):731-736.

[10]李岳,温熙森,吕克洪.基于核主成分分析的铁谱磨粒特征提取方法研究[J].国防科技大学学报,2007,29(2):113-116.

[11]何学文.基于支持向量机的故障智能诊断理论与方法研究[D].长沙:中南大学,2004:46-65.

[12]尹大伟.某型发动机模型修正研究[D].烟台：海军航空工程学院,2007:89-105.

[13]冯广斌,吴震宇,袁惠群.基于混沌理论与SVM的内燃机振动信号趋势预测[J].振动.测试与诊断，2011(1):64-69.

[14]胡金海,谢寿生,骆广琦,等.基于支持向量机方法的发动机性能趋势预测[J].推进技术，2005(3):260-264.

[15]郭磊.基于核模式分析方法的旋转机械性能退化评估技术研究[D].上海：上海交通大学，2009:56-77.

[16]Dimogianopoulos D,Hios J，Fassois S.Aircraft engine health management via stochastic modeling of flight data interrelations[J].Aerospace Science and Technology,2011(3):1-12.

[17]胡金海,谢寿生,骆广琦,等.基于支持向量机方法的发动机性能趋势预测[J].推进技术，2005(03):260-264.

[18]徐启华,师军.应用SVM的发动机故障诊断若干问题研究[J].航空学报，2005(6):961-967.

[19]许伟鸽,雷勇.某型航空发动机试车数据处理系统的设计[J].机械设计与制造，2008(12):73-75.

[20]李晓白,崔秀伶,郎荣玲.航空发动机性能参数预测方法[J].北京航空航天大学学报，2008(3):253-256.

(责任编辑：宋丽萍 英文审校：刘红江)

ResearchontheassessmentofengineperformancedeteriorationbasedonKPCA

TAN Wei1,XU Jian2，ZHANG Rui3

(1.Flight Theory Department,Naval Aviation Academy,Huludao 125001,China; 2.Navy Station in Shenyang Military Representative Office on Engine,Shenyang 110031,China；3.Mechanical and Electrical Engineering Shenyang Aerospace University,Shenyang 110136,China)

In order to assess the engine performance deterioration,a method of extracting engine parameter features is presented based on Kernel Principal Component Analysis(KPCA).Compared with the traditional KPCA,this method proposes a new classification of deterioration to solve the nonlinear problems in parameters,which realizes the dimensionality reduction and the preservation of main information of original parameters.It is worth of promoting in the synthesis of small sample nonlinear parameter index and dimensionality reduction.

performance deterioration;state assessment;KPCA;PCA

2013-11-26

谭巍(1982-)，男，湖北天门人，主要研究方向：发动机性能与测试，E-mail:twchy@sina.cn。

2095-1248(2014)03-0092-05

V235

A

10.3969/j.issn.2095-1248.2014.03.018