基于信息维数碳纳米管薄膜中碳纳米管分布均匀性评价方法

聂 鹏，高明圳，曾宪君，Ksenia lakovleva

(沈阳航空航天大学 机电工程学院，沈阳 110136)

基于信息维数碳纳米管薄膜中碳纳米管分布均匀性评价方法

聂 鹏，高明圳，曾宪君，Ksenia lakovleva

(沈阳航空航天大学 机电工程学院，沈阳 110136)

以分形理论为基础，以信息维数为测度对碳纳米管薄膜中的碳纳米管分散均匀性进行评价，运用MATLAB软件对碳纳米管薄膜SEM图像进行二值化，图像叠加，直线拟合等处理，求出直线的斜率，其斜率的绝对值即信息维数DI,将DI作为评定碳纳米管分布均匀性参数，其值越接近于2，其分布越均匀。将该理论应用于不同工艺下生产的碳纳米管薄膜，证明其可行性。

碳纳米管薄膜；信息维数；分布均匀性

碳纳米管(CNTs)自1991年Iijima[1]在高分辨率透射电镜下发现以来，由于其具有优越的电学、力学和化学性能而受到广泛关注。目前碳纳米管宏观体的制备，结构和潜在的应用研究已取得了一定的研究成果。在碳纳米管形成薄膜时，管与管之间相互搭接，形成网状结构，但由于碳纳米管分布不均匀，网状结构局部致密程度也会有所不同，对其各方面性能产生了巨大的影响。研究表明碳纳米管薄膜的均匀性是衡量碳纳米管复合材料质量的一项重要指标[2]。目前，碳纳米管薄膜普遍采用透射电镜(TEM)、扫描电镜(SEM)、原子力显微镜(AFM)、X射线衍射(XRD)对薄膜的表面质量进行微观定性的评定或采用混合制备后的纳米管复合材料的热力学、电学等性能进行间接评价。如W Zhou等利用拉曼光谱法对单壁碳纳米管有效地进行了表征[3]。刘兴辉等利用SEM观察碳纳米管表面形貌，再利用TEM对生物的结构进行观察[4]。袁寰等利用TG-DAT、XRD、SEM等对钝化的碳纳米管复合材料进行表征[5]。因此，建立一个定量的评价方法，对纳米薄膜的制备和应用具有重用的理论意义和实际应用价值。分形具有良好的标度不变性，对复杂图形和结构复杂的物质微观图像能够很好地进行定量表征[6]。杨英歌等[7]利用MATLAB等软件完成了分形维数计算程序的设计，并提取了纳米ZnO透射电镜像的分形图像，利用分形维数计算程序计算其分形维数，从而实现了定量描述纳米ZnO的形态。聂鹏等[8]基于盒维数对铁粉进行了分散性评价。王新鑫利用砂盒法和盒计维数对纳米银粉以及纳米TiO2等成功的进行了评价分析[9]。李鸿利，吴大鸣等应用分形方法对无机粒子/高聚物体系分散效果评价进行了研究[10]。分形是Mandelbrot在20世纪70年代表征复杂图像和复杂过程时提出的[11]。本文基于信息维数对碳纳米管薄膜进行定量评价。

1 理论分析

首先定义信息方程为

(1)

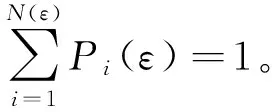
(2)

由于碳纳米管薄膜具有统计意义上的分形，因此本文将以该理论为基础对碳纳米管薄膜进行分形计算。将碳纳米管微观图像进行处理，每次以原盒子边长的1/2进行划分，划分若干次后，分别根据公式(1)、(2)进行计算，求出其信息维数。

信息维数作为一个分形体的空间维数，它应该小于所在空间的拓扑维数且越接近拓扑维数证明其分散越均匀[13]。本文中由于该图像为二维图像，因此该信息维数越接近2，其均匀性越好，即2-DI>0，且差值越小其分散越均匀。

2 参数提取

将图像用imresize函数转换为256*256的图像。由于纳米复合材料TEM图像通常存在背景亮度不均匀，碳纳米管边缘与背景难以区分的特点，因此需要对TEM图像进行相应的图像处理，形成高质量的二值图像，以便提取分散相颗粒图像的像素点数[14]。本文采用最大类间谱法对图像进行二值处理[15]。

利用meshgrid函数在图像上叠加方格，每一次的方格边长变化为原图像方格边长的1/2，经过若干次划分使得方格的边长趋近于0。

将图像二值化后，利用for循环将其变成点阵图像，通过编程统计出共有多少个点，每一次划分方格后，落在每一个方格中的点数占总点数的概率，并依据公式(1)计算出不同的I(ε),再将I(ε)与lnε利用最小二乘法进行直线拟合，所得直线的斜率的相反数即为目标图像的信息维数。

最后利用2-DI求其差值的大小，来判断该碳纳米纸薄膜中碳纳米管的分散均匀性。越趋于0，分散效果越好。

3 碳纳米管薄膜中碳纳米管分布均匀性参数提取实例

碳纳米管薄膜的完整制备过程是将碳纳米管与分散剂曲拉通(TX-100)按1∶4的比例混合进行研磨，使其充分接触，在将其加入500 ml的水中形成水溶液，再经过搅拌，超声破碎，高速离心机留取上清液，真空抽滤，水洗，高温固化等过程，形成碳纳米管薄膜。图1中(A)、(B)、(C)所示图片为未经过完整制备工艺生产出的薄膜，而图1(D)为经过上述完整加工工艺生产的薄膜。

图1 不同工艺条件下制备的碳纳米管薄膜的宏观图像和SEM图像

将以上SEM图像进行处理，应用到MATLAB编好的程序中，得到拟合曲线及值DI。

由图1(A)可以看出碳纳米管薄膜形成堆积，表面极不光滑，碳纳米管的分散最不均匀。由图1(B)可以看出，薄膜表面有破损，破损处无碳纳米管存在，因此碳纳米管的分布也相对不均匀。图1(C)未固化的碳纳米管表面产生了变形，宏观上看形成褶皱。图1(D)中的碳纳米管薄膜是通过完整工艺加工出的薄膜，具有最趋近于2的信息维数。

将图2、图3、图4、图5中的DI分别称为DA，DB，DC，DD，其信息维数分别为DA=1.7702303，DB=1.7888058，DC=1.8102929，DD=1.847477。1-DA>2-DB>2-DC>2-DD,由此可见其信息维数DI越接近于2，其碳纳米管在薄膜中的分布越均匀。

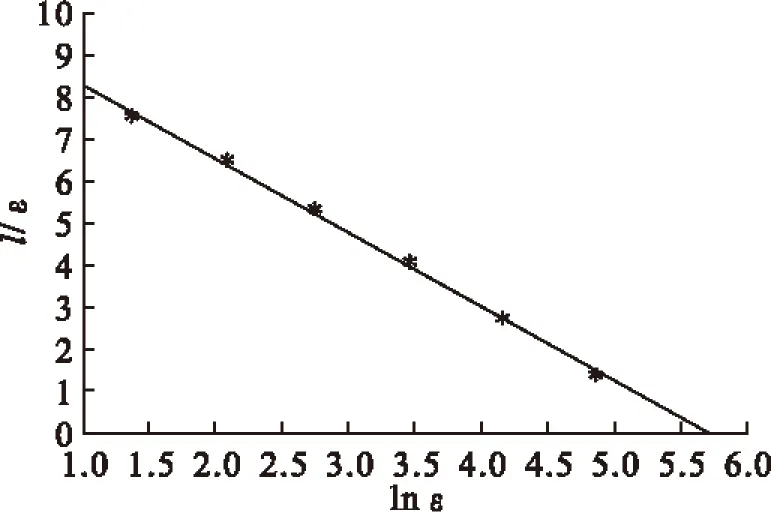
图2 图1-(A)维数DI的拟合曲线

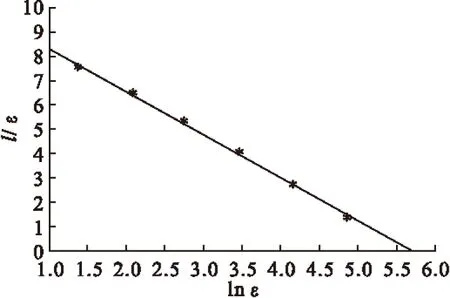
图3 图1-(B)维数DI的拟合曲线

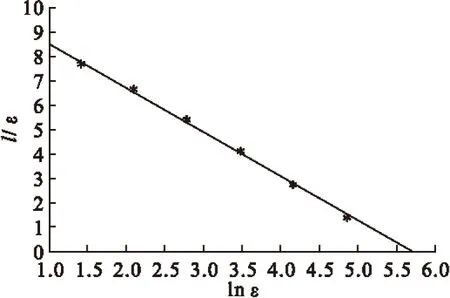
图4 图1-(C)维数DI的拟合曲线

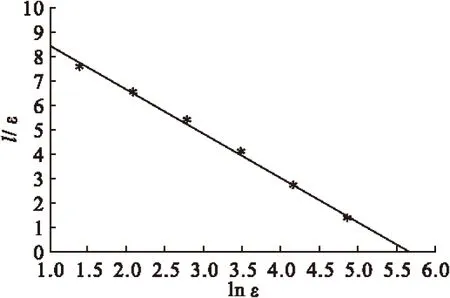
图5 图1-(D)维数DI的拟合曲线

4 结论

(1)本文提出的基于信息维数的模型能够正确评定碳纳米管薄膜中的碳纳米管分布均匀性；

(2)碳纳米管薄膜中碳纳米管分散均匀性的评价参数即信息维数DI均小于2；

(3)2-DI越趋于0，碳纳米管薄膜中碳纳米管的分布越为均匀。

[1]Iijima S.Helical microtubules of graphitic carbon[J].Nature,1991(354):56-58.

[2]徐均琪，易红伟，蔡长龙，等.磁控溅射膜厚均匀性与靶基距关系的研究[J].真空，2004,41(2)：25-28.

[3]W Zhou,Y.H Ooi,R Russo,P Papanek,D.E Luzzi,J.E Fischer.Structural characterization and diameter-dependent oxidative stability of single wall carbon nanotubes synthesized by the catalytic decomposition of CO[J].Chemical Physics Letters,2001,350(1):6-14.

[4]刘兴辉，朱长纯，田昌会，等.大面积碳纳米管复合材料的低温制备与表征[J].功能材料，2004,5(35):590-591.

[5]袁寰,廉永福,刘艳梅.单层碳纳米管的纯化与与其复合材料结构表征[J].齐齐哈尔大学报,2007,2(6):21-23.

[6]吕建国，陈学梅，朱剑博，等.Na参杂量对ZnO薄膜AFM图像多重分形谱的影响[J].电子显微学报2010,10,29(5)：415-419.

[7]杨英歌，吴润，从善海.分形图像分析及其在纳米ZnO中的应用[J].材料导报，2004,18(4):140.

[8]聂鹏，高霁，王新鑫，等.基于TEM图像和分形理论的纳米复合材料分散相粒度分布的评价方法研究[J].塑料工业，2004，32(1)：50.

[9]王新鑫.基于TEM图像和分形理论的纳米复合材料性能评价体系的研究[D].沈阳：沈阳航空航天大学，2009.

[10]李鸿利,吴大鸣,朱芬华,等.利用分形对无机粒子/高聚物体系分散效果的评定[J].塑料工业,2004,32(9):59-61.

[11]BB mndelbrot,The Fractal Geometry of Nature[J],New York,Freeman,1977,10:432-447.

[12]朱华，姬翠翠.分形理论及其应用[M].2011,1:48-49.

[13]石胜友，成明昊，郭启高等涪陵磨盘沟桫椤种群格局的分形特征-信息维数[J].西北植物学报,2004,24(7):1179-1183.

[14]聂鹏，王新鑫，高霁,等.纳米复合材料分散相分散均匀性的分形表征[J].北京航空航天大学学报,2009(7):852-855.

[15]Otsu N.A threshold selection method from grey-level histograms.IEEE Trans System[J].Man Cybernet,1079,SMC-9:62-66.

(责任编辑：吴萍 英文审校： 刘红江)

Evaluationmethodofcarbonnanotubesfilm′suniformitybasedoninformationdimension

NIE Peng,GAO Ming-zhen,ZENG Xian-jun,Ksenia LAKOVLEVA

(College of Electromechanical Engineering,Shenyang Aerospace University,Shenyang 110136)

Based on the fractal theory,the uniformity of carbon nanotube dispersed in carbon nanotube film is measured by the information dimension.With the MATLAB software,the SEM images of carbon nanotube film are processed with the methods of binarization,overlapping and fitting.And the absolute value of the straight line gradient,i.e.the information dimension,is calculated.The information dimension is made as the parameter of carbon nanotubes distribution uniformity.The closer its value is to 2,the more even the distribution of the carbon nanotubes is.Its feasibility was proved by the production of carbon nanotube film under different process.

carbon nanotube film;information dimension;distribution uniformity

2014-03-07

辽宁省航空科学基金(项目编号：2012ZD54)

聂鹏(1972-)，男，吉林吉林人，博士，教授，主要研究方向：航空试验与测试，E-mail:niehit@163.com。

2095-1248(2014)03-0049-04

TP206+.1

A

10.3969/j.issn.2095-1248.2014.03.010