薄壁结构约束阻尼板减振降噪优化设计

张彩霞，沙云东，朱 琳，揭晓博

(沈阳航空航天大学 a.能源与环境学院;b.航空航天工程学部，沈阳 110136)

薄壁结构约束阻尼板减振降噪优化设计

张彩霞a，沙云东b，朱 琳b，揭晓博b

(沈阳航空航天大学 a.能源与环境学院;b.航空航天工程学部，沈阳 110136)

针对薄壁结构约束阻尼减振降噪问题，采用耦合有限元和间接边界元的方法对约束阻尼层厚度进行了优化设计。根据声辐射功率与结构表面振动速度之间的关系，选取振动速度的平方和作为目标函数，各层厚度和总质量分别作为设计变量和状态变量，对一块四角固定的矩形约束阻尼板进行优化仿真，并对优化前后的约束阻尼板进行振动和声学响应分析。结果表明，约束阻尼层厚度配置对阻尼减振有确定性定量影响关系，优化后声辐射功率得到明显降低。

薄壁结构;冲击载荷;约束阻尼层;振动;噪声

为减轻重量航空航天飞行器上大量采用薄壁结构，如飞行器蒙皮、发动机燃烧室等,它们常常因受到随时间变化的冲击载荷的作用而产生较大的结构振动和噪声。工程中经常采用敷设约束阻尼的方式来减小结构振动和噪声[1-10]，并通过优化的方法使阻尼性能和经济效益最大化,因此对冲击载荷作用下薄壁结构约束阻尼减振降噪优化设计的研究具有重要的现实意义。

约束阻尼的减振降噪优化包括两个方面：一是对结构动力特性进行优化；二是对结构振动响应进行优化。在结构振动特性方面，杨雪等[6]研究了各阻尼层材料的几何及物理参数对阻尼结构性能的影响,并对粘弹性阻尼材料和弹性钢板组合成的阻尼板进行了优化设计；沈允文等[5]用有限元结合模态应变能的方法，进行结构阻尼最佳敷设位置的预测；陈学前等[8]采用有限元结合损耗因子最大化的方法，对约束阻尼板各层厚度进行了优化。杨加明等[9]运用改进遗传算法结合损耗因子最大化的方法，对多层黏弹性复合材料结构进行优化设计。在结构振动响应方面，史蒙等[10]对结构重量进行重新分布来减小结构振动和噪声辐射；SEMYUNG WAND等[11]通过灵敏度分析方法改变结构几何尺寸来降低结构辐射声功率。

本文从结构振动响应出发，采用耦合有限元和间接边界元的方法对三层约束阻尼结构各层厚度进行了优化设计。包括四方面内容：一是对结构施加冲击载荷并进行完全瞬态分析得到结构时域的振动速度；二是对结构振动速度进行傅里叶变换和功率谱分析；三是优化设计算法及编程；四是计算优化前后结构的声学响应，并对响应结果进行分析和比较。结果表明本文的方法可以有效的减小结构振动和噪声辐射。

1 结构振动和声辐射理论

1.1 冲击载荷下的响应

冲击载荷作用下结构的运动方程为[12]:

(1)

式中，ω0为结构的自振圆频率；ξ为结构的阻尼比；F(t)为外激励向量。

当系统输入为F(t)，初始位移为零时:

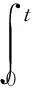
(2)

由(2)式可得结构的振动位移响应，对其进行傅里叶变换并求导可以得到结构和流体交接面的节点法向振动速度V(x,ω)。

1.2 间接边界元声学分析

流体介质是连续的，所以认为结构表面振动速度就是临近表面一层流体的振动速度[13]。设结构表面任意一点声压为P(y,ω)，则：

(3)

式中，r为结构表面任意两点x和y的距离；ρ为空气密度；c为声速。

于是结构表面的声辐射功率达式为:

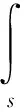
(4)

可以看出，结构对外辐射的声功率是速度的二次性函数。

2 约束阻尼层厚度优化设计

2.1 优化设计原理

优化问题的数学模型可以表示为[14]。

minf(x)=f(x1,x2,…,xn)

(5)

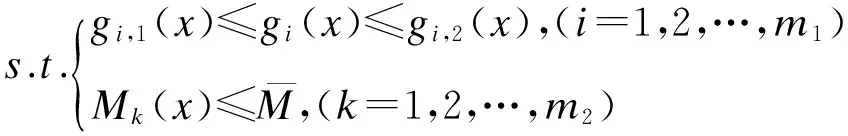
(6)

式中，f(x)是目标函数，优化的最终目标是得到目标函数的极小值。gi(x)和Mk(x)分别是设计变量和状态变量，它们对优化起到约束的作用，在约束范围内的设计才是有效的。本文根据(4)式中声辐射功率与结构表面振动速度之间的关系，选取结构表面各节点法向振动速度平方和为目标函数、各层厚度为设计变量、结构总质量为状态变量对结构进行优化。

2.2 优化设计方法

利用一阶方法进行优化求解。一阶方法在每次迭代过程中依赖目标函数对设计变量的偏导数，将约束问题通过罚函数法转化为无约束问题，即强制设计变量和状态变量的界限，用最大斜度法或共轭方向法确定搜索方向，并用线搜索法使非约束问题最小化，计算得到新的设计变量集，再执行分析文件，最后判断它是否收敛。

无约束化问题是把目标函数和约束函数按照一定的方式构成一个新函数，这样就使得原来有约束优化问题就变成了无约束优化问题[15]。初值的选取采用内点发，即初始点在可行域内，则罚函数如下：

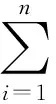
(7)

Px,Pg,PM分别是设计变量和状态变量的罚函数；r是罚因子。

本文的优化流程图如图1所示：

3 约束阻尼层厚度优化算例

3.1 约束阻尼结构有限元模型及载荷形式

研究对象为三层矩形约束阻尼板。阻尼板四角固定，板长1 000 mm，宽600 mm，基层、粘弹性层、约束层的厚度分别为h1,h2,h3。基层和约束层的材料密度为2 763 kg/m3，杨氏模量为73.11 GPa，泊松比为0.32。这里不考虑粘弹性材料弹性模量和损耗因子受温度和频率的影响，根据经验取杨氏模量为270 MPa，损耗因子为0.1，泊松比为0.49，密度为1 780 kg/m3。

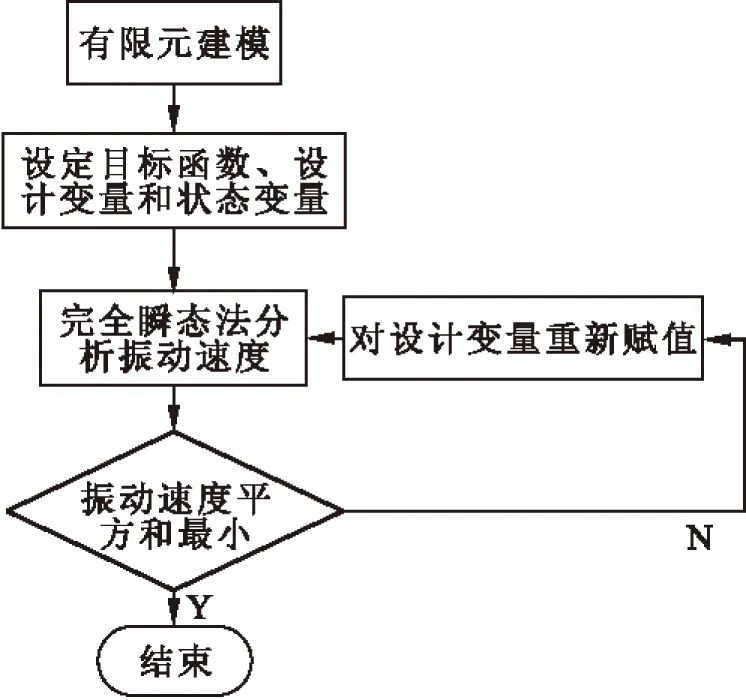
图1 约束阻尼振动速度最小优化流程图

有限元模型如图2所示，基层、粘弹性层和约束层分别采用向上偏心shell181单元、 solid185单元和向下偏心shell181单元，三层通过共用节点连接在一起。在板中心169点施加100N的冲击载荷，载荷时域曲线如图3所示。

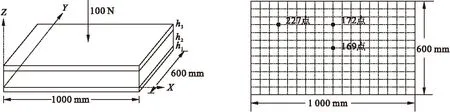
图2 约束阻尼板有限元模型

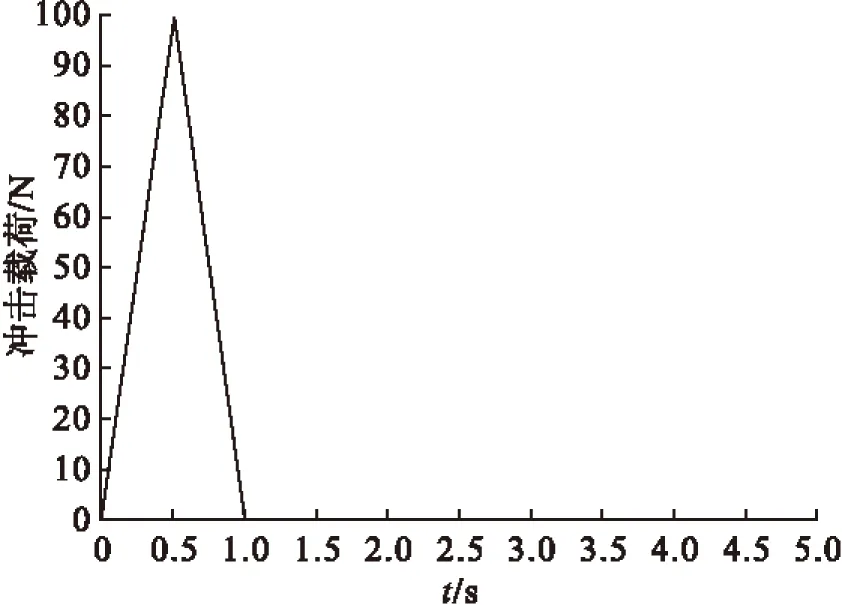
图3 冲击载荷时域曲线

3.2 阻尼层厚度优化设计及分析

优化设计以各层厚度为设计变量，结构总质量为状态变量。依据机械工程手册和前期工作经验，设计基层的范围从1 mm到4 mm；粘弹性层从5 mm到20 mm；约束层从0.1 mm到2 mm；总质量不大于29.2 kg。以各节点速度平方和为目标函数，根据(5)和(6)式，该问题的数学模型为：

(8)

(9)

上述模型中，Vj,k为结构在第j个频率时第k节点的振动速度；W为频率总数；N为有限元模型节点总数；h1,h2,h3分别为基层，粘弹性层和约束层的厚度；M是结构总质量。在本算例中M满足下面方程：

M=1.6578h1+1.068h2+1.6578h3

(10)

设计h1,h2,h3的初值分别为2 mm、13 mm、0.8 mm，对169号节点施加如图3所示的一幅值为100 N的时域冲击载荷，采用一阶方法进行优化求解，经过8次迭代后得到各层厚度最优配置，如表1所示。

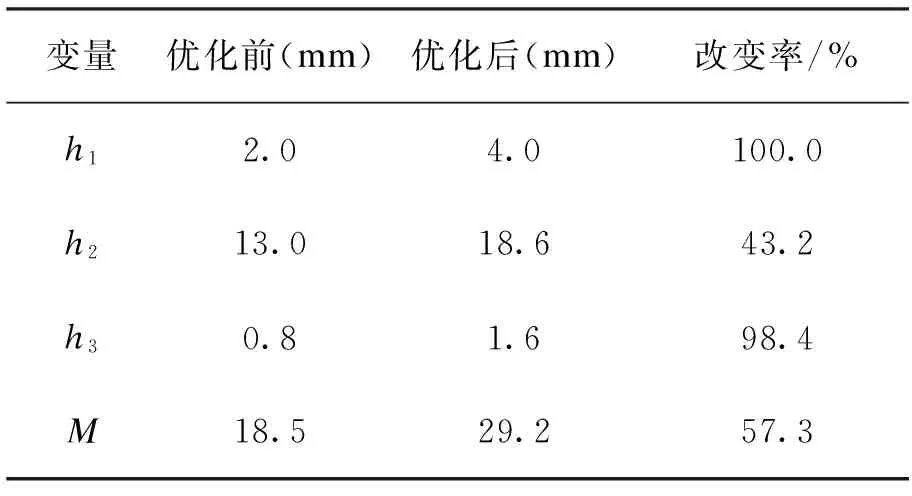
表1 优化前、后设计和状态变量参数

分别对优化前、后结构的前10阶模态进行求解，并提取前四阶振型。优化后结构的第一阶固有频率增大了13.07 Hz，模态对比见表2，振型见图4、5。

表2 优化前、后前10阶模态频率(Hz)对比表

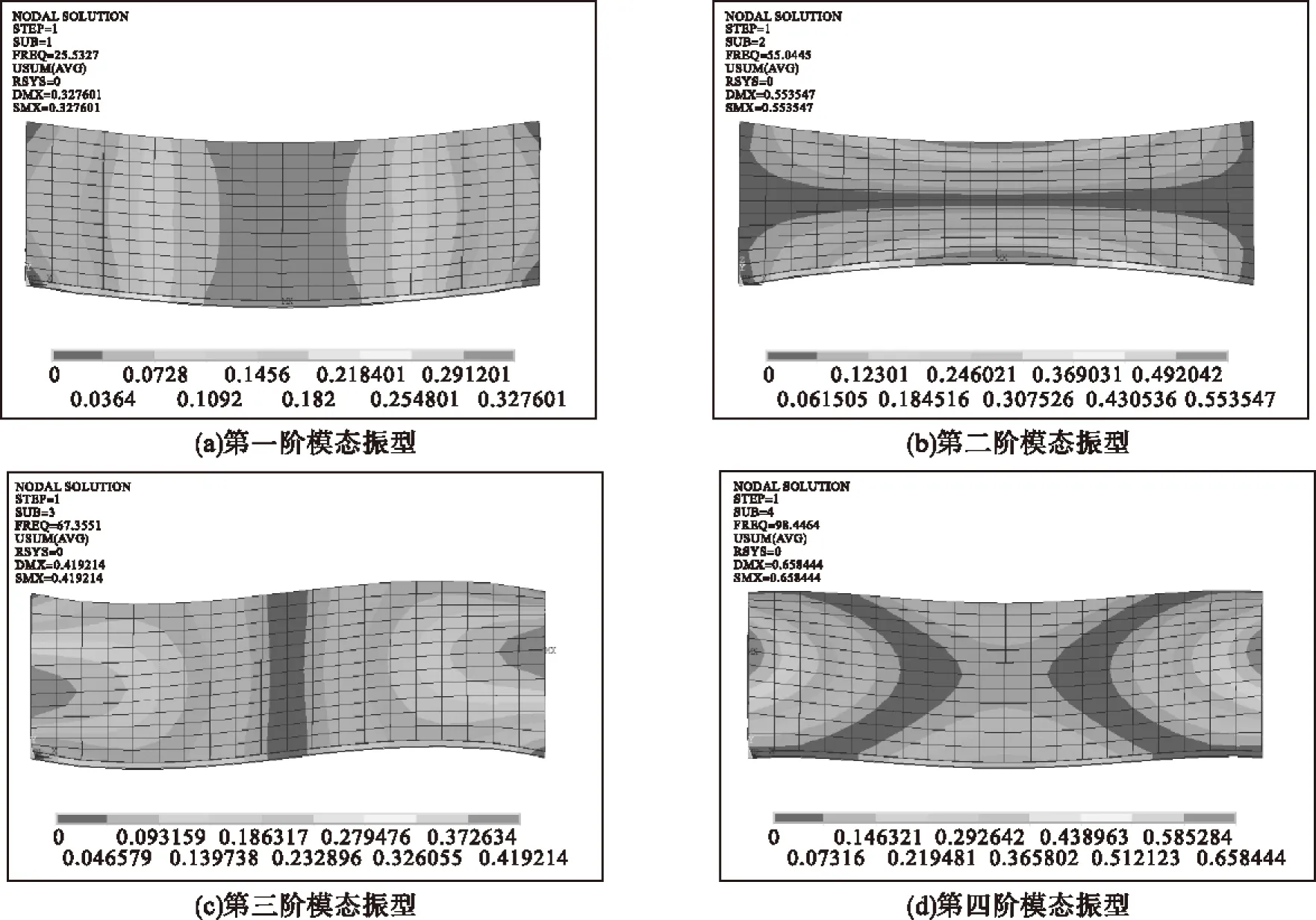
图4 优化前前四阶模态振型

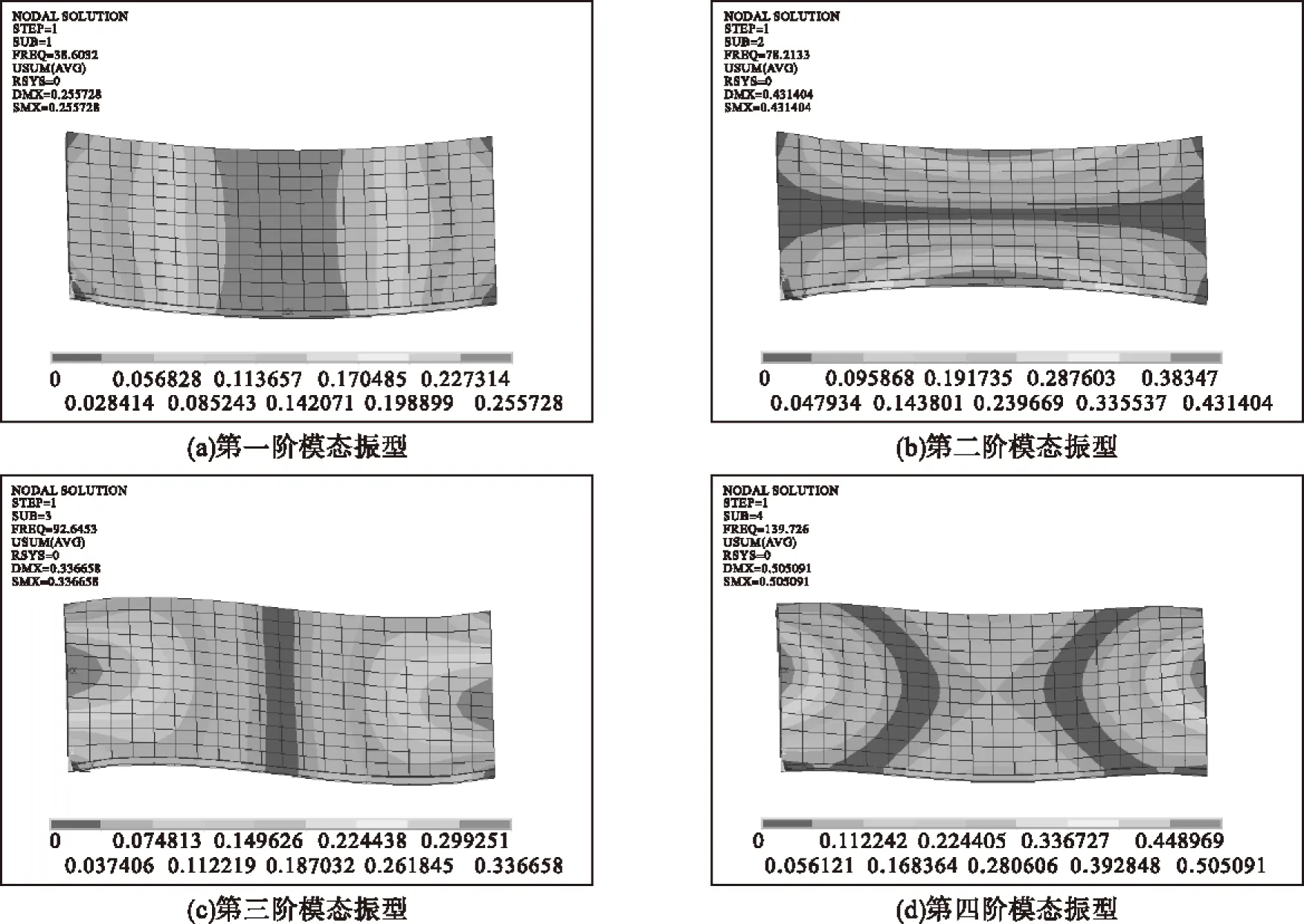
图5 优化后前四阶模态振型

选取有限元模型的169、172和227点作为特征节点，它们的位置如图2所示。提取优化前后三个特征节点的振动速度响应，并求其功率谱密度。图6和7可以看出，优化后振动速度最大赋值从1.5×10-2降到4.5×10-4m/s，振动速度减小了两个数量级。对比优化前后功率谱密度，如图8和9所示，1 Hz到70 Hz频率范围内减少了一阶共振频率，振动能量也明显降低。

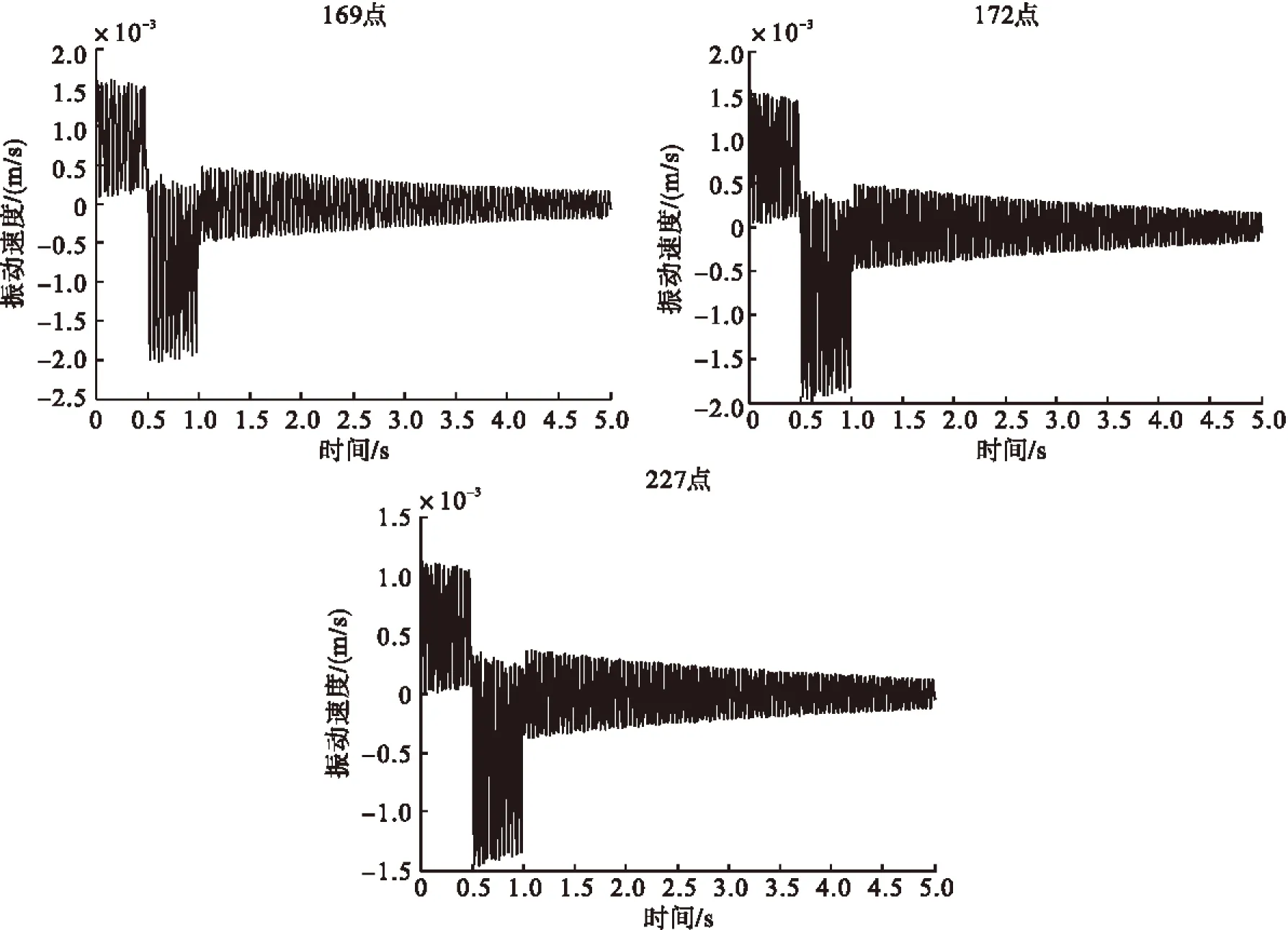
图6 优化前各特征节点振动速度时域曲线

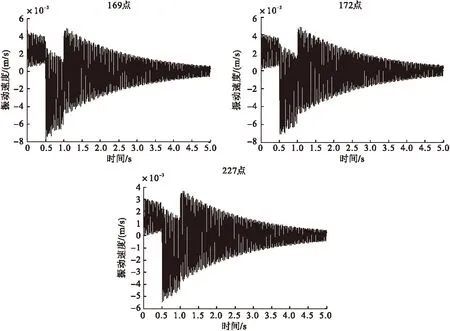
图7 优化后各特征节点振动速度时域曲线

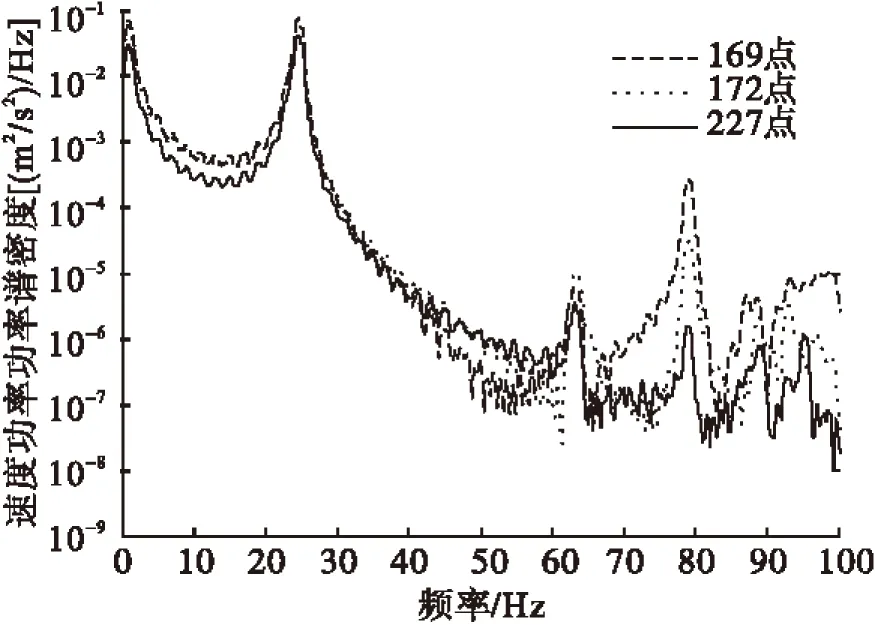
图8 优化前特征点速度功率谱密度

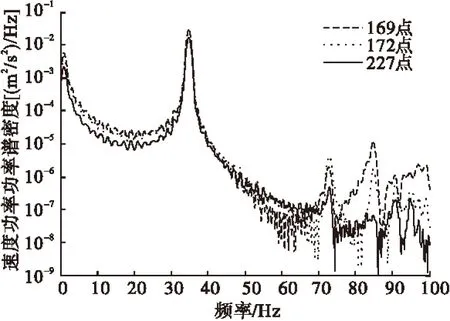
图9 优化后特征点速度功率谱密度

3.3 优化前/后约束阻尼结构声学分析

以上面计算得到的振动速度为边界条件，构造边界元模型，如图10所示。优化前、后的声辐射功率级如图11所示，能够看到20 Hz处声辐射功率级降低了10 dB左右。

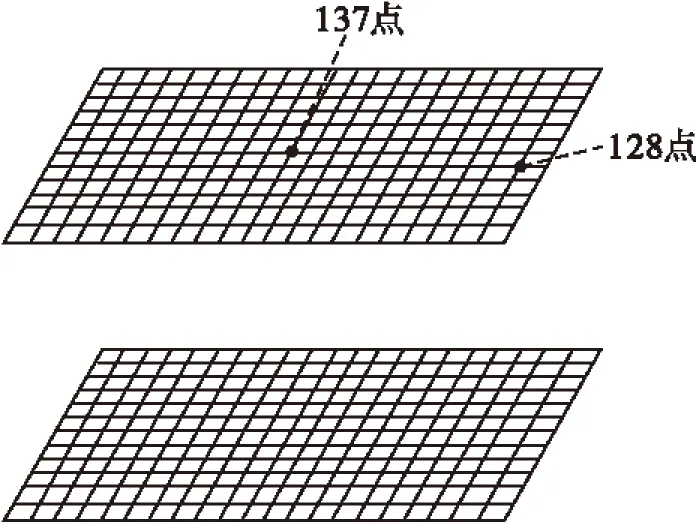
图10 边界元模型及域面网格

在距离薄板表面500 mm的位置建立长1 000 mm，宽600 mm的平面声场网格,如图10所示。平面场点137和128在优化前、后频域的声压级如图12、13所示。对比发现几乎所有频率的声压级都得到降低，137场点最大声压级减小了6 dB，128场点最大声压级减小了4 dB左右。

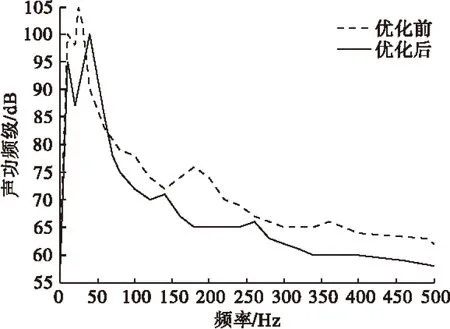
图11 优化前、后声辐射功率级

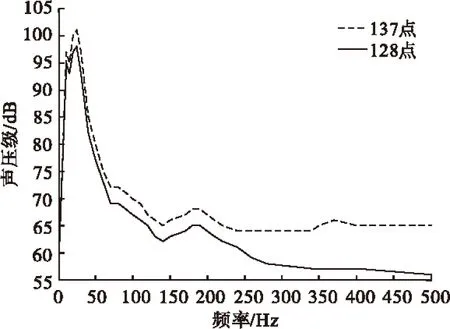
图12 优化前特征场点声压级

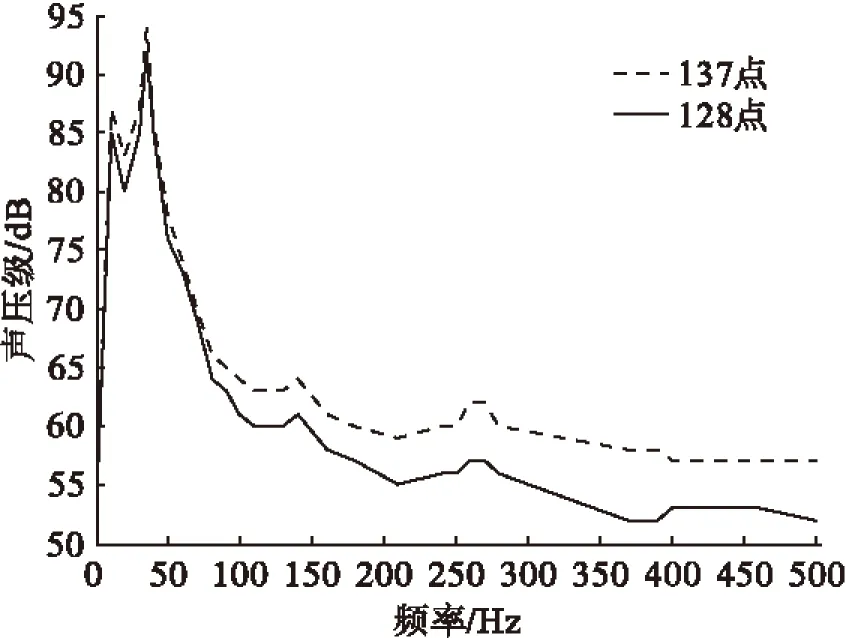
图13 优化后特征场点声压级

4 结论

(1)研究表明声辐射功率与结构振动速度的大小直接相关。因此可以通过寻找最小振动速度的方法对约束阻尼结构进行优化设计；

(2)采用一阶方法对约束阻尼质量和厚度进行优化，能够很快的确定搜索方向，罚函数法将约束问题转化为无约束问题，针对约束阻尼结构各层厚度优化问题采用一阶方法结合罚函数法，可以快速准确的得到最优解；

(3)研究发现约束阻尼层厚度配置对阻尼减振效果有确定性定量影响关系。本文的优化方法可以对质量和厚度有严格要求的约束阻尼板进行优化，也可以为具有其他约束条件的约束阻尼优化提供参考。

[1]Xisheng Cao，Hans-Peter Mlejnek.Computational prediction and redesign for viscoelastically damped structures[J].Computer Methods in Appllied Mechanics and Engineering，1995，125：1-16.

[2]R.Moreira，J.D.Rodrigues.Constrained damping layer treatments:finite element modeling[J].Journal of Vibration And Control，2004，10：575-595.

[3]Sainsbury,M.G.and Zhang,Q.J.The Galerkin Element Method Applied to the Vibration of Damped Sandwich Beams[J].Computers and Structures,1999,71(3):239-256.

[4]Chen,Q.and Chan,Y.W.Integral Finite Element Method for Dynamical Analysis of Elastic-viscoelastic Composite Structures[J].Computers and Structures,2000,74(1):51-64.

[5]李鸿秋，陈国平，张保强.考虑声振耦合下结构阻尼板降噪拓扑优化设计[J].振动、测试与诊断，2011,31(5):586-590.

[6]杨雪，王源升，朱金华.二层粘弹阻尼复合结构的优化设计[J].海军工程大学学报，2003，15(4)：69-72.

[7]沈允文，李树庭.阻尼夹层结构减振的最佳阻尼位置预测[J].西北工业大学学报，1995，13(3)：331-335.

[8]陈学前，杜强，冯加权.运用有限元分析的阻尼板优化设计[J].振动、测试与诊断，2007，27(3)： 236-238.

[9]杨加明，张义长，吴丽娟.多层黏弹性复合材料结构阻尼性能优化设计[J].航空学报，2011，32(2)： 265-270.

[10]史蒙，张军，方吉,等.FEM /BEM法振动板减振降噪优化设计[J].大连交通大学学报，2009,30(2)：1-5.

[11]SEMYUNG WAND，JEAWON LEE.Acoustic design sensitivity analysis and optimization for reduced exterior noise[J].AIAA Journal，2001，39(4)：1237-1245.

[12]徐定海，盖京波，王善.冲击载荷作用下板壳结构的可靠性研究[J].机械设计，2009，26(2)：66-67.

[13]任开勋.机身蒙皮铆接噪声辐射特征及阻尼减振降噪技术研究[D].沈阳：沈阳航空航天大学，2011.

[14]韦勇，陈国平.一般阻尼结构的模态阻尼优化设计[J].振动工程学报，2006，19(4)：433-437.

[15]马骋，李迅，姚家晖，等.一种新的求解带约束的有限极大极小问题的精确罚函数[J].应用数学和力学，2012,33(2):250-264.

(责任编辑：吴萍 英文审校：刘红江)

Optimizationdesignofthin-walledstructurewithconstraineddampinglayer

ZHANG Cai-xia1，SHA Yun-dong2，ZHU Lin2，JIE Xiao-bo2

(1.College of Energy and Environment;2.Faculty of Aerospace Engineering,Shenyang Aerospace University,Shenyang 110136,China)

Finite element and indirect boundary element methods are used to optimize the design of thickness of each layer to reduce the vibration and acoustic radiation power.Based on the relationship between acoustic radiation power and vibration velocity of the surface of structure,the square of the vibration velocity is selected as objective function,and the thickness of each layer and the total mass of structure as design variable and state variable.A constrained damping plate with four corners fixed has been simulated and optimized.The results shows that the configuration of thickness has a definite and quantitative effect on damping.The optimization makes the vibration velocity and acoustic radiation power reduced significantly.

thin-walled structure;impact loadings;constrained damping layer;noise

2013-11-06

张彩霞(1988-)，女，辽宁辽阳人，硕士研究生，主要研究方向： E-mail:617321997@qq.com;沙云东(1966-)，男，黑龙江阿城人，教授，主要研究方向：发动机强度震动与噪声，E-mail:ydsha2006@vip.sina.com。

2095-1248(2014)03-0032-07

V214.19

A

10.3969/j.issn.2095-1248.2014.03.007