框架箱涵的力学特性研究及参数分析

张海涛 王 锦

随着交通系统的发展，交通线路的下穿或者跨越的情况越来越频繁，地下通道成为了一种简单又经济的方案选择。同时出于对景观、环境的考虑，为了减少汽车、人流等地面交通的影响，也使得地下通道的应用发挥了越来越大的作用[1,2]。

对于通道的结构设计，设计人员最常用的方法是取1 m通道的展向长度，将其简化为二维的平面框架进行内力计算，在此基础上对结构进行受力分析和配筋[3]。在多数形状规则、斜交角度较小的情况下，这样的简化计算经证明是合理的。但随着地下通道实用造型的需要，可能会出现大斜交角的情况，以往的一些研究结果已表明，采用上述的简化方法计算得到的结果与实际斜交情况下的受力存在较大偏差，容易造成不安全因素。与此同时，一些对地下结构产生直接影响的因素，包括地基条件以及分孔布置等，如何合理模拟这些参数的影响，对于计算的精细化而言都是非常关键的问题，而以往对此并未见详细的研究。

本文通过采用相比梁单元更为精细的板壳单元模型对斜交箱涵的空间受力进行了数值模拟，总结了随斜交角增加结构内力的变化趋势。并对地下通道设计中的关键参数地基系数和分孔尺寸进行了一定范围内的定性研究，由此对其影响总结出规律。再在这些规律的基础上对结构方案中的参数设计提出合理化建议。

1 计算模型与参数设置

1.1 计算模型

本文计算模型取自某工程实例，并根据研究目的进行适当简化处理。项目中由于通道口存在交通线汇合，所以箱体的截面由三孔逐渐过渡到两孔，实际工程中也多存在两孔和三孔两种构造，故本文计算模型共涉及了这两种典型的断面形式，如图1所示，其中Δ为中孔跨径。

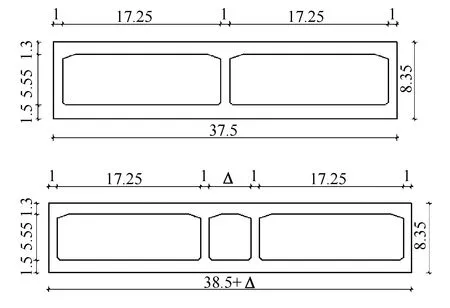
图1 框架箱涵断面图(单位：m)Fig.1 Frame box culvert cross sections (Unit: m)

如图1所示，由交通流量控制的单孔净跨为17.25 m，箱体靠近外侧为人行道，内侧为单向三车道，孔洞净高5.55 m，顶板厚设为1.3 m，底板厚为1.5 m，竖墙厚为1 m，这些尺寸都是设计初步拟定的尺寸。通道顶地下埋深2 m，三孔的中孔为空置状态，没有实际交通用途。

为了考虑斜交角度对内力的影响，本文用六自由度板单元对斜交角下的箱体进行了空间受力分析，模型如图2所示。模型保持通道的有效使用宽度为18.75 m不变，通道段长为30 m，其中θ为斜交角。

如图2所示，模型选择9个点作为控制节点，提取其内力变化。其中，1，1′，1″为顶板靠近中墙位置，2，2′，2″为顶板靠近外墙位置，3，3′，3″为顶板跨中位置。而1′，2′，3′是在箱体纵向中分线上，其余两组在箱体两端。

1.2 计算荷载

计入的恒载除了结构自重，还包括顶板上覆土重及通道内铺装、栏杆的重量，侧墙所受的土压力按规范取主动土压力[4]，采用梯形荷载输入，实际工程没有地下水的影响，单孔荷载分布示意如图3所示。

图2 斜交框架计算模型(单位：m)Fig.2 Skew frame computational model (Unit: m)

图3 计算荷载示意图Fig.3 Computational loads

汽车荷载按公路一级计算。另外，考虑顶板后浇混凝土收缩效应，按顶板降温15 ℃处理。

1.3 计算参数设置

本文主要涉及的设计参数包括斜交角度θ、地基系数k0和箱室布置(中孔尺寸大小)。

其中计算的斜交角度有0°、10°、20°、30°、40°、50°，以充分考虑随斜交角增大的内力变化；计算了5种不同级别的地基系数，考虑随地基刚度增加底板内力的变化；为了验证箱室大小布置对内力分布的影响，在保证边孔尺寸不变的情况下，计算了中孔宽度为0 m、2.5 m、5 m、8.5 m、15 m、17.25 m、22 m、25 m的情况以考虑其增大效应。

2 计算结果分析

2.1 斜交角度的影响

本节以两孔箱涵为背景对斜交角度的影响进行了讨论，为了方便对计算结果进行对比，选取了如图2所示的9个控制节点。不同算例保证顶板的垂直有效跨度不变，按斜交的角度计算顶板的受力。需要说明的是，中间墙体上下端顶底板的弯矩峰值仅作不同算例之间的对照，直接取用的模型计算结果，并没有进行弯矩的顶上削峰折减。此处计算使用的地基系数为10 000 kN/m3，而关于地基系数的详细影响在后面再作进一步讨论。

由图4可见，随着斜交角度的增加，弯矩的极值在增加，弯矩的分布也越来越不均匀，峰值逐渐向两端的自由边集中，且跨中弯矩最大值方向保持与自由边垂直，导致Y坐标不同位置处的横向弯矩分布差别越来越大。如果此时仍按照简化的二维平面框架进行计算，显然与实际情况不符。

图5所示为各控制点处的弯矩随斜交角度变化的曲线图。由图5(a)可见，点1～1″处的最大负弯矩，钝角处和中部的弯矩都在逐渐增大，而锐角处的弯矩逐渐减小，由于1和1″实际是在中墙同点两侧的弯矩，却出现了相反的发展趋势，可见随着斜交角的增加，中墙顶部分担的弯矩也在逐渐增加。图5(b)所示为顶板两端的负弯矩变化，可见，随着斜交角增加，钝角处2″的负弯矩迅速增大，而锐角处的弯矩缓慢减小，甚至在最后出现了正弯矩，相比之下中部节点2′处的弯矩变化不大。图5(c)所示的是跨中最大正弯矩的变化趋势，可见，随着斜交角的增加，3′和3″处的弯矩都迅速减小，3处的弯矩随着斜交角的增加变化趋势比较特别，首先是增大，但随后到40°之后又减小，这种现象在图4的云图中表现很直观，接近箱体两端锐角处的应力集中现象越来越明显，而以往研究中也都出现过相似情况[5,6]。

图4 顶板横向弯矩分布云图随斜交角增加的变化Fig.4 Cross-structure bending moment nephogram of the top-plate with increasing skew angles

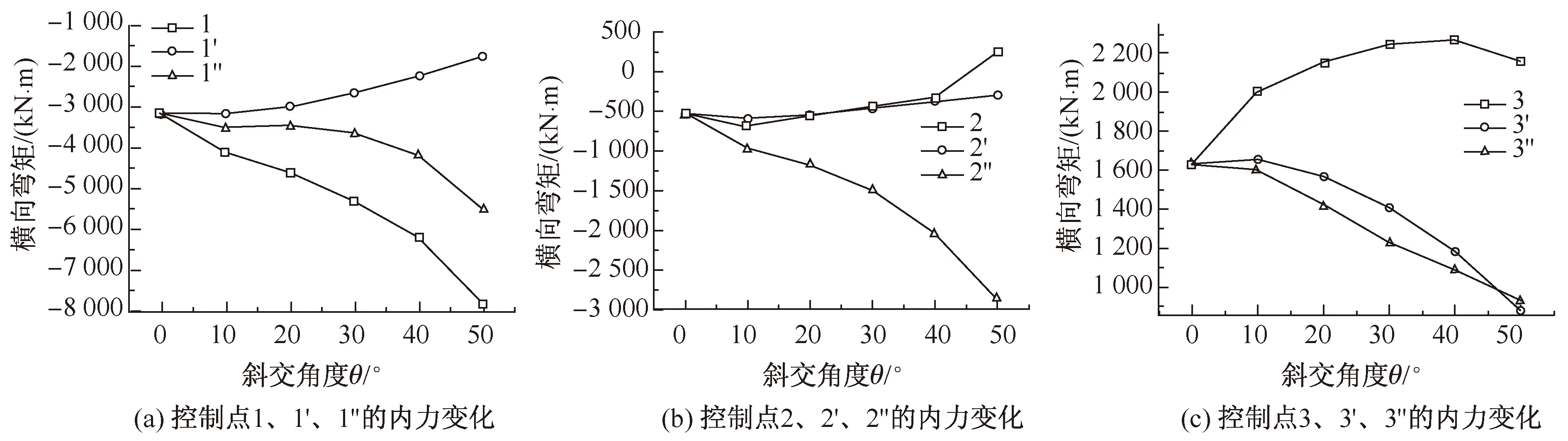
图5 顶板横向弯矩随斜交角增加的变化Fig.5 Cross-structure bending moment of the top-plate with increasing skew angles

由上可知，随斜交角增加钝角区域的应力集中现象最为明显，而锐角区和中部段有卸载的现象。所以，在设计钝角位置的配筋时也应该加强以满足受力需求，且最好双向配置。

2.2 地基系数的影响

基于文克尔弹性地基梁的假定，地基对箱涵底的作用可以视为连续弹性支撑，在计算中可以用地基土弹簧模拟基础的支撑作用，弹簧刚度与地基土的刚度有关，用地基系数k0表示[7]。地基系数随不同种类土质的变化很大，为了讨论不同地基条件对结构内力的影响，以下采用了几种常见的土体类型，其参数如表1所示。

表1几种土质的地基系数参考值[7]

Table1ReferencevaluesoffoundationmaterialcoefficientskN/m3

土名淤泥质土、新填土软弱黏性土碎石土普通砂岩地基系数0.5×1041×1041.5×1051×106

此处为了增加对比位置采用的是三孔箱体模型，如图6所示，选用了5对控制节点提取了内力值，其中1～5分别代表底板上靠近外墙位置、边孔跨中位置、靠近中墙两侧位置和中孔跨中位置，1′～5′则对应顶板上的上述位置。计算结果与以往研究都表明[8]，地基系数对底板的受力影响较大，对顶板的受力则几乎没有影响，故以下主要对比了底板的计算结果。

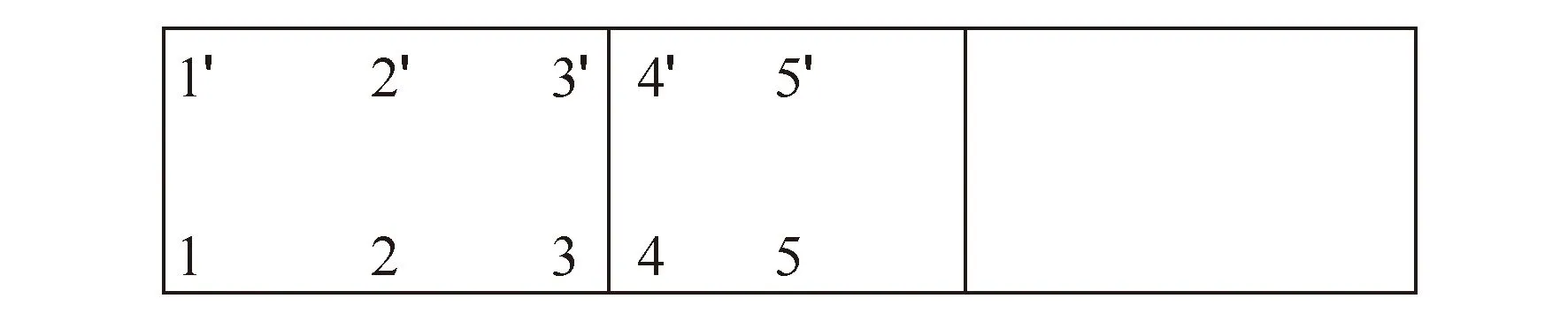
图6 顶底板控制节点示意图Fig.6 Control nodes on the top and bottom plates

图7所示为箱体底板传递给下部地基的压力。首先可知，地基压力的总和是一定的，承受着上部传递的全部恒、活载，地基系数的影响表现为对压力分布的改变。

图7 基底压力随地基系数变化情况Fig.7 Base pressure with increasing base coefficients

可以看到，当地基系数较小时，压力分布是均匀平缓的，这是因为地基较“软”能够和底板共同变形。随着地基系数的增加，压力逐渐变得不均匀，特别是墙体连接处的力会迅速增大，代表地基土对底板的限制作用也越来越强，这样在需要承受传递较大上部荷载的部位，如图中所示的控制节点1、3、4处和承受较大汽车荷载的区域，压力的作用都要明显高于传力较小的其他部位。

由于地基作用直接影响了底板受力，图8给出了随地基系数改变底板弯矩包络图的变化情况。可以看到，与图7中所示的情况相对应，地基系数越大，底板内力就越小，直到地基系数为1×106kN/m3时，跨中的板内力已经非常接近于0了，内力变化也趋于均匀。当然在直接承受顶板荷载的各墙肢墙底，局部受力还是较大的。另外，可以看到随着地基系数的增大，控制节点3和4处的内力差越来越大，这是由于底板抗变形能力的增加，导致墙底分配的弯矩更大，这时候就需要特别注意墙底的配筋布置能不能够满足需求。

图8 底板弯矩随地基系数变化情况Fig.8 Bending moment of the bottom-plate with increasing base coefficients

由上可知，地基系数越大，也就是地基的抗变形能力越强，可以缓解底板所受的弯矩，却导致基底反力更加的不平均，局部压力过大增加了地基设计处理的困难。

2.3 箱室尺寸的变化

在实际工程应用中，三孔箱体与两孔同样是一种常见的截面型式，本工程的中间孔虽无实际交通需求，但中孔的受力依然有这种截面的代表特性，同时中孔尺寸变化对框架整体的受力也会产生影响。此处，对不同中孔跨度的受力作计算以研究这种影响的变化。此处依然采用了图6中的模型，并采集了5对控制节点的内力值。

如图9所示，底板中孔的弯矩受中孔跨度的影响较大，而边孔的内力则基本没有发生改变。其中中墙墙底处3点、4点的弯矩首先是下降之后又增加，是因为最初由单墙传递的上部力分为双墙传递时削弱了底板的弯矩尖峰，但随后由于中孔跨度的增加，导致这部分的削弱很快被填补回来。而5点处的弯矩则有一个很明显的增加趋势。

图9 底板弯矩随中孔跨度变化Fig.9 Bending moment of the bottom-plate with increasing middle-box widths

图10所示的顶板内力变化与底板有相似的情况，比如边孔的1′点、2′点处弯矩变化较小，2′点处的弯矩出现了小幅的减小，其实是由于中孔荷载的反向“翘起”作用引起的；3′点、4′点处的弯矩也出现了先减小后增加的趋势，而中孔跨中5′点的内力则几乎是线性增加的，这与底板5点处的情况不太一样，5点内力在增加到一定程度之后就趋于水平，是因为中孔底板上没有直接作用荷载，而顶板的覆土作用会随着净跨一直增加。另外，可以看到顶板上覆土作用导致3′点、4′点处荷载增长趋势的改变，在中孔跨度为22 m时两点弯矩基本相同，也就是说此时墙顶中的弯矩接近0，进而可知墙顶弯矩随中孔跨度的变化趋势。

图10 顶板弯矩随中孔跨度变化Fig.10 Bending moment of the top-plate with increasing middle-box widths

由上可知，单孔受力状态影响最大的是本孔内的跨中弯矩，孔两端的弯矩由于和相邻孔顶底板的变形协调，增长趋势较为缓和，同时墙体的上下端弯矩大小和方向也会因为相邻两孔跨度的比例改变而改变。

3 结论与建议

通过对地下通道箱涵建立空间板壳模型和简化杆系模型进行有限元计算，并考虑重要结构参数的影响趋势后，可得到如下主要结论：

(1) 对于斜交箱体而言，斜交角度对箱体的受力影响较大，特别是随角度增加简化的杆系模型不能考虑到钝角附近出现的应力集中现象，计算结果偏于不安全。这时候，最好能够采用空间板壳模型进行整体计算，以充分考虑结构整体的受力及配筋。

(2) 地基系数对计算结果的影响较大，既影响了底板的受力和进一步配筋工作，同时影响了地基的设计、处理，加之影响土的力学特性的因素复杂难以确定，其数据上的参考价值就大打折扣，所以当条件满足时最好能够根据详细的地勘结果确定。

(3) 箱孔的尺寸分配对该孔的内力影响较大，主要是跨中的正弯矩最明显，而对边孔的内力影响较小，增加孔空间及孔数量提高箱体的利用率从受力来讲并不会造成更大的设计困难，是一种可选的方案。

(4) 由于算例的限制，本文并没有考虑多个因素的综合影响，比如斜交和地基系数、箱室布置的共同变化等，但大致可以根据本文结论进行推论。不管是箱内行车的地下通道还是顶板行车的地道桥，对于结构受力的特点而言是没有差别的，所以此处所作的结论对于其他用途的相似结构也是通用的。参考以上计算得到的一些规律，可以对箱体的设计特别是方案初选进行合理的布置。

[ 1 ] 李鹏，黄怡.城市人行天桥与地下通道方案设计及比选[J]. 城市道桥与防洪,2006(6):25-28.

Li Peng, Huang Yi. Design comparison and selection of urban pedestrian overpass and underpass scheme[J]. Urban Roads Bridges and Flood Control, 2006(6): 25-28. (in Chinese)

[ 2 ] 刘韵.城市地下快速道路建设动因分析[J]. 地下空间与工程学报,2006(S2): 1293-1296.

Liu Yun. Analysis on motivation of urban underground fast-driving road construction[J]. Chinese Journal of Underground Space and Engineering, 2006(S2): 1293-1296. (in Chinese)

[ 3 ] 李家稳. 地道桥设计与施工[M]. 北京：中国铁道出版社, 2011.

Li Jiawen. Design and construction of underpass bridge[M]. Beijing: China Railway Publication House, 2011. (in Chinese)

[ 4 ] 中交公路规划设计院.JTGD60-2004公路桥涵设计通用规范[S]. 北京: 人民交通出版社,2004.

CCCC Highway Planning and Design Institute. General code for design of highway bridges and culverts[S]. Beijing: China Communications Press, 2004. (in Chinese)

[ 5 ] 王庆贵.斜交框架地道桥的参数分析[J].盐城工学院学报(自然科学版),2013, 26(1): 75-78.

Wang Qinggui. Parameters analysis of skew frame underpass bridge[J]. Journal of Yancheng Institue of Technology (Natural Science Edition), 2013, 26(1): 75-78. (in Chinese)

[ 6 ] 谢敏杰.某大斜交角度框架地道桥的设计与分析[J]. 石家庄铁道大学学报(自然科学版),2012, 25(2): 15-18.

Xie Minjie. Design and analysis of large skew angle framework bridge[J]. Journal of Shijiazhuang Tiedao University (Natural Science Edition),2012, 25(2): 15-18. (in Chinese)

[ 7 ] 姜伟，袁勇，柳献.地下结构中混凝土结构边界约束效应分析[J]. 结构工程师, 2011, 27(1): 61-65.

Jiang Wei, Yuan Yong, Liu Xian. Boundary restraint of concrete structures during underground construction[J]. Structural Engineers, 2011, 27(1): 61-65. (in Chinese)

[ 8 ] 王丽，季日臣，伊新芳，等.斜交框架地道桥的力学特性[J]. 甘肃科学学报,2009, 21(1): 132-134.

Wang Li, Ji Richen, Yin Xinfang, et al. Mechanic character of frame tunnel bridge with skew angle[J]. Journal of Gansu Science, 2009, 21(1): 132-134. (in Chinese)