预应力结构小比例模型设计方法探讨
2014-08-27任祥香卢文胜
任祥香 卢文胜
1 引 言
目前,国内外振动台模型试验的一般过程为[1-3]:根据相似关系设计并制作与原型结构相似的模型结构;对模型结构进行试验;将模型结构的动力特性和动力反应通过相似关系反推到原型;最后对原型结构的抗震性能进行评价。可见,相似关系的正确性是确保试验有效性的关键,只有在保证相似关系正确的前提下,模型试验研究才是有意义的。
理论上,当影响结构性能的各因素均能满足经典相似理论的要求时,原型结构的动力特性和动力反应可以通过模型结构来准确模拟。但在小比例结构模型相似设计时,由于受振动台性能、材料的力学性能等方面的制约,传统相似关系的严格要求与现有的试验及相关技术能力具有严重的不可调和性。为此,国内外研究者着力于研究一些实用相似方法,在长期的研究过程中得出一些适用于限制条件下的相似试验方法并在模型试验中得到广泛的应用[3-6]。
然而,对于预应力结构而言,小比例模型相似设计方法依然匮乏,现有的相似方法试验模拟的效果还不是很理想。虽然近年来也不乏预应力结构地震模拟振动台试验的研究工作[7,8],但这些试验研究多是针对整体结构性能开展的,很大程度上忽略了预应力结构构件的相似要求。因此,预应力结构的相似关系需要进一步的研究。
2 结构模型相似关系
结构模型振动台试验中的相似关系可从材料、构件和整体结构三个层面上进行讨论。
2.1 基于材料层面的相似关系
基于材料层面的相似关系从构成结构的材料出发,依据材料的物理力学性能参数,运用量纲分析法或方程式分析法进行模型结构的设计并用于模型试验。其一般方法为:基于材料弹性模量相似常数SE、几何相似常数SL和密度相似常数Sρ,通过量纲分析法推导出其他物理量的相似常数进行相似设计。理论上,这种由材料特性相似保证整体结构相似的方法能够满足结构模型弹性阶段的相似要求,但在实际操作中具有相当的难度[9]。
2.2 基于构件层面的相似关系
基于构件层面的相似关系[4]从构件变形和承载能力分析的角度上,强调构件力学性能的相似。可控相似常数选用几何相似常数SL、变形相似常数Sd、构件控制截面承载力相似常数SM、加速度相似常数Sa及重力加速度相似常数Sg,并通过这5个基本量纲根据似量纲分析方法确定其他相似常数。该方法能够保证构件在弹性阶段的相似性,而当构件进入弹塑性阶段,结构构件内力和变形发生重分布时,要同时满足承载能力和刚度的相似性则需要把握构件关键截面非线性性能。
2.3 基于结构层面的相似关系
基于结构层面的相似关系强调结构动力特性和动力反应的相似。在进行模型设计时,结合试验目的,直接控制结构参数来把握模型与原型动力特性和动力反应的相似。其中,动力特性主要涉及结构的自振频率、质量和阻尼;动力反应主要涉及结构的弹塑性变形、位移角、剪重比和加速度反应等。
在把握构件层面相似关系的基础上,这种直接由结构动力特性和动力反应的相似保证结构相似的方法可以保证结构在弹性阶段和弹塑性阶段的相似。
3 预应力结构相似关系探讨
预应力结构模型模拟地震振动台试验应实现整体结构与模型结构特性和动力反应的相似,并在此基础上确保预应力构件的相似。
3.1 整体结构相似关系表达
基于结构层面的相似关系可控相似常数一般可选用几何相似常数SL、刚度相似常数SK、质量相似常数Sm、弹性模量相似常数SE和力相似常数SF。在静力试验中SL,SK和SE可以确定其余相似常数;在动力试验中确定重力加速度相似常数后,根据SL,SK,Sm和SE可以确定其余相似常数。根据具体试验参数的获取方法不同,可将SK或Sm转化为动力特性相似常数St。基于结构效应的模型试验相似关系可以表达如表1所示。
表1基于结构效应的模型试验相似关系
Table1Generalformsofsimilarityrelationsbasedonstructuraleffects
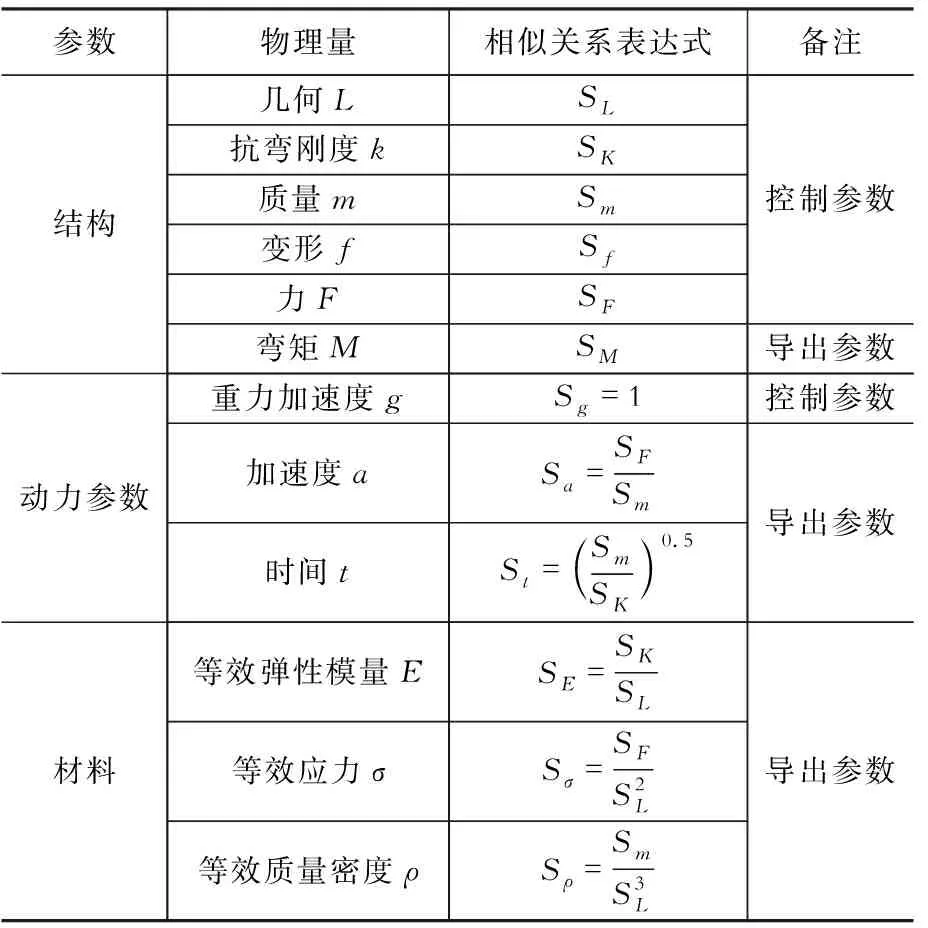
参数物理量相似关系表达式备注结构几何L抗弯刚度k质量m变形f力F弯矩MSLSKSmSfSFSM控制参数导出参数动力参数重力加速度g加速度a时间tSg=1Sa=SFSmSt=SmSK 0.5控制参数导出参数材料等效弹性模量E等效应力σ等效质量密度ρSE=SKSLSσ=SFS2LSρ=SmS3L导出参数
3.2 预应力混凝土结构相似关系
基于结构效应的相似关系需要根据不同的试验对象及试验目的具体分析,以选取合理参数进行相似设计。针对预应力混凝土结构模型,本文提出基于“预应力作用效应”相似的设计方法,即控制结构参数,在保证模型和原型结构预应力构件荷载—位移关系曲线相似的基础上,进行材料选择和截面参数的确定。
该相似方法主要有两个优点:一个是荷载—位移关系曲线是预应力构件刚度性能变化的重要反映,预应力构件中预应力的损失、裂缝的产生等原因导致的刚度下降都将体现在位移反应上;另一个优点是荷载—位移关系曲线的相似不仅可以保证弹性阶段的相似,还可以保证部分构件屈服进入弹塑性阶段后的相似。
4 基于“预应力作用效应”的预应力构件相似设计方法
本文采用现行规范中的刚度模型,分两阶段对预应力混凝土梁进行挠度相似分析。
4.1 未开裂阶段相似关系
未开裂状态下的预应力混凝土截面刚度降低系数取为0.85。预应力梁在集中力F作用下的挠度为
(1)
同样,对模型结构有:
(2)
根据式(1)、式(2),可推导出挠度相似常数为
(3)
可得:
SEc=SF·SL-1·Sf-1
(4)
式中 上标为p代表原型,上标为m代表模型;
S——挠度计算公式系数;
F——施加在梁上的集中力;
L——预应力梁长度;
Bs——预应力梁的等效抗弯刚度;
Ec——混凝土弹性模量;
I0——预应力梁截面惯性矩。
4.2 开裂阶段相似关系
预应力梁受拉区混凝土开裂后,引入折减系数μ来考虑混凝土开裂对梁刚度的影响,则:
Bs=μ0.85EcI0
(5)
(6)
(7)
Mcr=(σpc+γftk)W0
(8)
式中Bs——预应力梁的等效抗弯刚度;
Ec——混凝土弹性模量;
kcr——预应力梁截面的开裂弯矩Mcr与外荷载F产生的弯矩Mk比值;
αE——钢筋弹性模量与混凝土弹性模量的比值;
ρ——纵向受拉钢筋的配筋率;
γf——受拉翼缘面积与腹板有效面积的比值;
σpc——扣除全部预应力损失后在抗裂验算边缘的混凝土预压应力;
γ——混凝土构件的截面抵抗矩塑性影响系数;
ftk——混凝土的抗拉强度标准值。
由以上公式可以看出,受拉区混凝土开裂后的刚度相似关系应该在满足开裂前的相似关系的基础上,保证折减系数μ的相同。则由式(5)—式(8)可推得:
(9)
式中A——预应力梁的截面面积;
Ap——预应力钢筋面积。
化简式(9)可得:
(10)
综上所述,设计预应力混凝土梁模型结构时,如果预应力钢筋设计满足相似准则(4)、(10),则该模型与原型的预应力“结构效应”相似。
对预应力混凝土结构,基于结构层面的相似关系更为合理。一方面,预应力混凝土结构由混凝土、钢材等多种材料组成,由于各种材料相似性的不协调,实际模型中基于不同材料的相似关系可能不同,即一个模型中存在多个材料相似关系,但基于结构层面的宏观反应的相似关系只有一个。另一方面,振动台模型试验大多是针对整体结构,随着试验对象体量的增大,缩尺比例也越来越小,加上预应力混凝土结构受力机制较为复杂,基于材料层面的传统相似关系更加难以应用。
4.3 预应力结构相似关系表达
运用量纲分析法,基于“预应力作用效应”相似关系可以补充如表2所示。
表2预应力结构相似关系表达式
Table2Generalformsofsimilarityrelationsofprestressedstructures
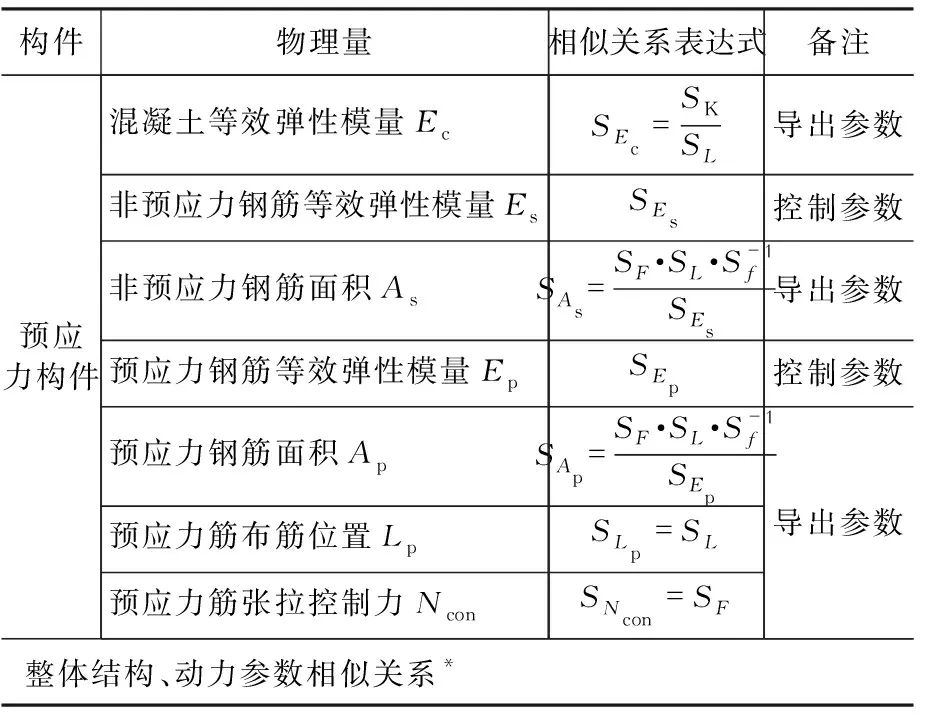
构件物理量相似关系表达式备注预应力构件混凝土等效弹性模量Ec非预应力钢筋等效弹性模量Es非预应力钢筋面积As预应力钢筋等效弹性模量Ep预应力钢筋面积Ap预应力筋布筋位置Lp预应力筋张拉控制力NconSEc=SKSLSEsSAs=SF·SL·S-1fSEsSEpSAp=SF·SL·S-1fSEpSLp=SLSNcon=SF导出参数控制参数导出参数控制参数导出参数整体结构、动力参数相似关系*
注:整体结构、动力参数相似关系参见表1。
5 大跨预应力结构小比例模型设计实例
5.1 工程概况
某文化艺术中心主楼为框架-剪力墙混凝土结构体系。如图1和图2所示,结构总高度为45.9 m,标高23.2 m处至屋顶层为一端悬挑的三向预应力混凝土结构。其中,典型楼层沿悬挑方向布置12根预应力大梁,悬挑长度为9.35~17.54 m。该建筑位于7度抗震设防区。

图1 典型楼层预应力结构平面布置图Fig.1 Typical layout of the prestressed elements

图2 建筑剖面图Fig.2 Structural configuration profile
为研究结构在不同水准地震作用下的整体抗震性能,考察可能存在的薄弱部位,对该结构进行模拟地震振动台试验。
5.2 相似模型设计
该工程对悬挑部分施加预应力的主要目的在于提高构件的抗裂性、延缓裂缝的开展并减小裂缝宽度。预应力效应在结构层面上表现为减小该悬挑部分在竖向荷载作用下的位移。因此,在进行模型设计时,可将悬挑端的位移作为衡量结构效应的参数,并保证模型与原型之间的结构响应(位移)的相似。因此,先选择该结构J-2轴线与J-3轴线间的一根预应力混凝土悬挑梁(图3)为设计对象,对该相似设计方法进行验证。
5.2.1原型预应力混凝土梁
结构混凝土强度等级为C50;预应力钢绞线采用低松弛钢绞线,规格为φ5×7;非预应力钢筋采用HRB400级钢,材料参数如表3所示。预应力张拉采用应力-应变双控,控制应力为0.75fptk。具体参数如表3所示。
计算得该梁的开裂弯矩585.7 kN·m,极限弯矩Mu为1 463.3 kN·m。在梁端部施加集中力F,F从零逐步增加直至梁破坏过程中,力与梁端位移的关系曲线如图4所示。
5.2.2相似设计
为确保该预应力大悬挑混凝土框架-剪力墙结构模拟地震振动台试验顺利进行,综合考虑原型结构和试验室条件,采用缩尺比例为1/30的模型进行模拟地震作用下的动力试验。

图3 预应力悬挑梁示意图(单位:mm)Fig.3 Schematic diagram of the prestressed cantilever beam (Unit: mm)
表3预应力梁材料力学性能指标及参数
Table3Materialsmechanicalperformanceindexoftheprestressedbeam

混凝土预应力钢绞线fc/MPaftk/MPaEc/MPafptk/MPafpy/MPa-23.12.643.45×1041 8601 320-预应力钢绞线非预应力钢筋Ep/MPaAp/mm2fy/MPaAs/mm2Es/MPaAs'/mm21.95×1054 35536014 4762.00×10512 867
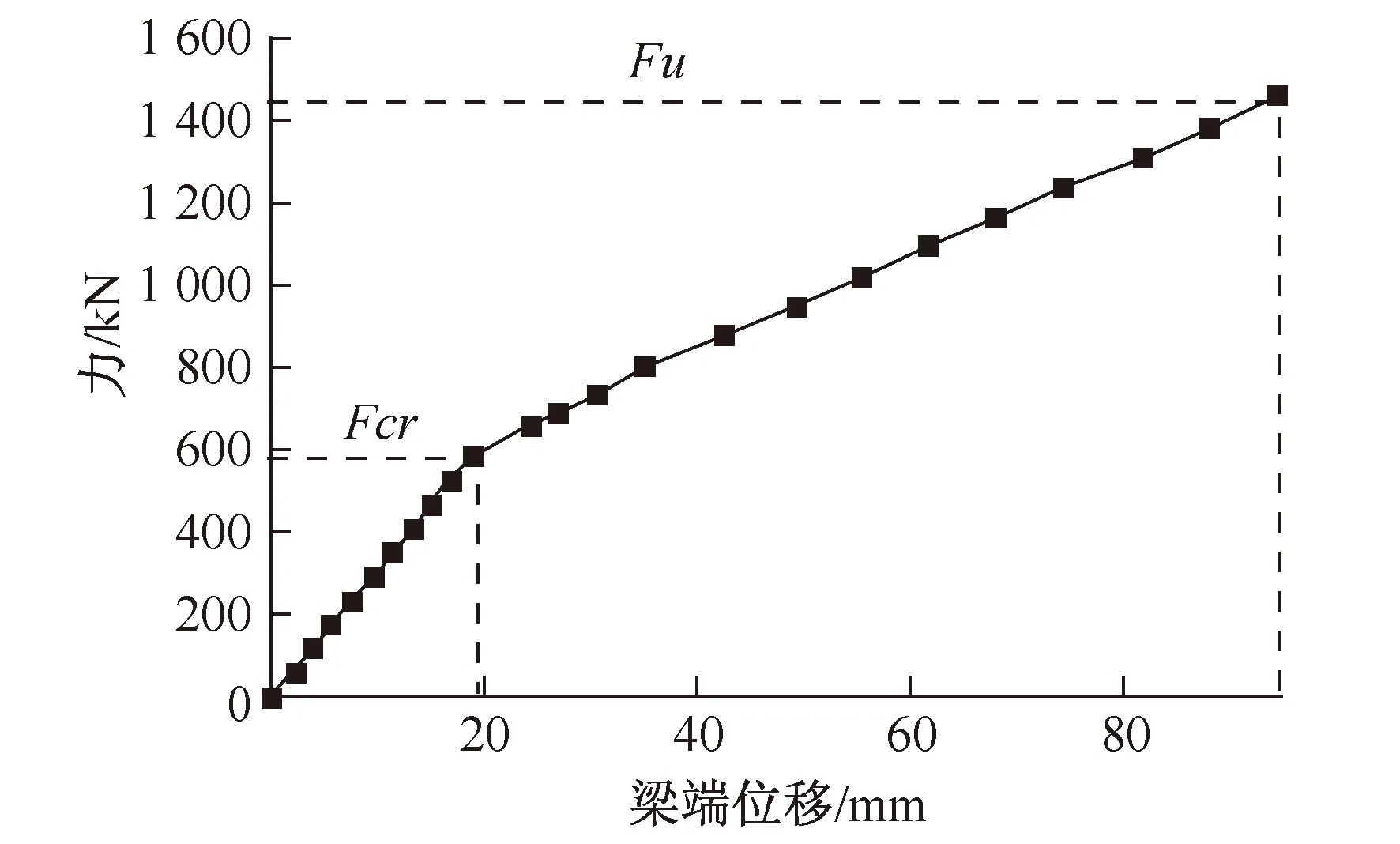
图4 预应力悬臂梁力—位移关系曲线Fig.4 Load-displacement curves of the prestressed cantilever beam
模型用微粒混凝土制作。微粒混凝土是一种模型混凝土,它是由细骨料、水泥和水组成的专门用于结构模型试验的材料。一般采用2.5~5.0 mm的粗砂代替普通混凝土中的粗骨料砾石;用0.15~2.5 mm的细砂代替普通混凝土中的细骨料砾石,并按一定级配和水灰比组成。通过调整配合比控制微粒混凝土弹性模量与原型混凝土弹性模量相似比为0.2。在模型制作过程中同时浇筑规定数量的砂浆立方体试块和棱柱体试块以测定微粒混凝土材料的强度和弹性模量。
模型钢筋采用回火镀锌铁丝;预应力钢绞线采用玻璃纤维筋(GFRP)模拟;非预应力钢筋采用HRB400级钢筋。控制结构参数保证梁端力—位移关系曲线相似,从而达到模型结构与原型结构的“预应力效应”相似,具体相似常数如表4所示。
表4模型和原型相似常数
Table4Similarityrelationbetweenthemodelandtheprototype
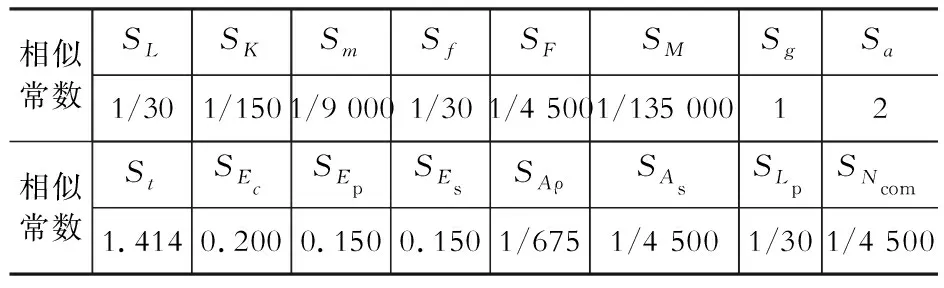
相似常数SLSKSmSfSFSMSgSa1/301/1501/9 0001/301/4 5001/135 00012相似常数StSEcSEpSEsSAρSAsSLpSNcom1.4140.2000.1500.1501/6751/4 5001/301/4 500
根据表2所示的相似关系进行模型设计,设计完成后模型的尺寸及预应力筋的布置位置如图5所示;模型材料及相关配筋面积如表5所示。

图5 预应力悬挑梁模型示意图(单位:mm)Fig.5 Material parameters and the reinforcement area of the model beam (Unit: mm)
表5模型材料参数及配筋面积
Table5Materialparametersandareaofthereinforcementofthemodelbeam

微粒混凝土混凝土GFRPfc/MPaftk/MPaEc/MPafptk/MPaσef/MPaEp/MPaAp/mm24.620.530.69×104900207.73.00×1046.50非预应力钢筋fy/MPaEs/MPaAs/mm2As'/mm22802.00×1053.202.56
5.2.3模型结构计算分析
根据现有预应力纤维聚合物混凝土结构的研究成果[10],计算GFRP预应力混凝土悬臂梁模型的挠度。梁的刚度采用双直线法。未开裂状态下刚度降低系数仍采用0.85;受拉区混凝土开裂后的截面刚度:
(11a)
(11b)
(12)
式中Bs——模型梁的等效抗弯刚度;
Ec——微粒混凝土弹性模量;
kcr——模型梁截面的开裂弯矩Mcr与集中力F产生弯矩Mk的比值;
αE——钢筋弹性模量与微粒混凝土弹性模量的比值;
ρ——纵向受拉钢筋的配筋率;
λ——预应力度;
σpc——预应力筋在受拉区边缘混凝土产生的有效预压应力;
σsc——短期荷载在混凝土边缘产生的拉应力。

(13)
(14)


SM——模型结构与原型结构弯矩相似常数,见表4。
δ1和δ2随着截面的不同而变化,其对应原型构件各截面的分布规律如图6所示,其中x为截面与固定端的距离。
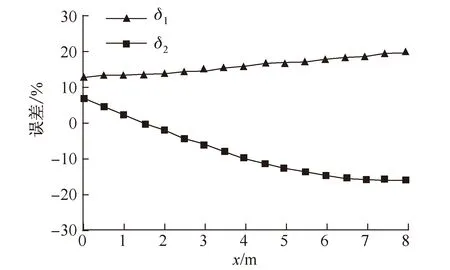
图6 模型和原型间误差分布Fig.6 Distribution of errors between the model and the prototype
同样,模型结构的力-位移关系曲线可通过表2中的相似关系反推,得到一条模型结构的推算曲线。将推算曲线与4.2.1节中原型结构的力—位移计算曲线相比较,如图7所示。

图7 模型反推原型的弯矩—位移关系曲线Fig.7 Load-displacement curve of the prototype
分析上述计算结果可知:
(1)不同截面处模型的开裂弯矩和极限弯矩与原型结构误差保证在20%以内,具有较好的相似性。
(2)相对于原型结构,模型受拉区混凝土开裂和截面破坏均较晚。
(3)在混凝土未开裂阶段和开裂阶段,模型的力-位移关系曲线与原型误差均保持在15%以内,较为吻合。
(4)预应力梁进入开裂后,在相同力作用下,模型推算出的挠度要小于原型。在对原型结构进行性能评定时要充分考虑这方面的因素。
可见,基于“预应力效应”相似的设计方法是有效的,且在模型中采用玻璃纤维增强聚合物替代原型中的预应力钢绞线是可行的。
5.3 大跨预应力结构1/30模型设计
依据表4中的相似常数,对该大悬挑预应力混凝土结构进行1/30的缩尺模型设计。在模型设计时尽可能满足模型与真实结构几何特性、构件和节点构造、荷载分布等方面的相似规律。然而,必要时要根据设计计算分析,在确保正确模拟主体结构性能的前提下,对主体结构作一定的简化设计,如简化不规则的洞口、次梁及次要楼层等。据此制作完成的模型结构如图8所示。

图8 模型全景Fig.8 Model view
6 结 论
本文在总结现有结构模型相似设计方法的基础上,提出了基于“预应力效应”相似的设计方法。采用该方法设计了某预应力混凝土框架-剪力墙结构1/30的缩尺模型,并通过实例对该方法进行验证。
(1) 控制模型结构与原型结构力—位移关系曲线相似,推导出实际操作中便于实现的预应力构件的相似准则,并通过实例说明其具体应用。
(2) 不同于传统设计方法,首次提出在模型中采用玻璃纤维筋(GFRP)模拟原型结构的预应力钢绞线。
(3) 计算结果表明,该方法设计的模型梁与原型梁的开裂弯矩及极限弯矩的误差在20%以内;混凝土进入开裂阶段后,梁的力—位移关系误差保证在15%以内,保证了较好的相似性。
[ 1 ] 吕西林,邹昀,卢文胜,等.上海环球金融中心大厦结构模型振动台抗震试验[J].地震工程与工程振动,2004,20(3):57-63.
Lu Xilin, Zou Yun, Lu Wensheng, et al. Experimental study on Shanghai Finacial Center[J]. Earthquake Engineering and Engineering Vibration, 2004, 24(3): 57-63. (in Chinese)
[ 2 ] 李检保,吕西林,卢文胜,等.北京LG大厦单塔结构整体模型模拟地震振动台试验研究[J].建筑结构学报,2006,27(2):10-14,39.
Li Jianbao, Lu Xilin, Lu Wensheng, et al. Shaking table model test of Beijing LG building[J]. Journal of Building Structures, 2006,27(2): 10-14,39. (in Chinese)
[ 3 ] 王栋,卢文胜,吕西林.某高位转换框支剪力墙超限高层结构模拟地震振动台试验研究[J].振动与冲击,2013,32(21):142-149.
Wang Dong, Lu Wensheng, Lu Xilin. Shaking table test of a high-rise frame-supported shear wall structure with a high transfer floor[J]. Journal of Vibration and Shock, 2013, 32(21):142-149. (in Chinese)
[ 4 ] 周颖,吕西林,卢文胜.不同结构的振动台试验模型等效设计方法[J].结构工程师,2006,22(4):37-40.
Zhou Ying, Lu Xilin, Lu Wensheng. Shaking table test model design in different structures[J]. Structural Engineers, 2006,22(4):37-40. (in Chinese)
[ 5 ] Kim N S, Lee J H, Chang S P. Equivalent multi-phase similitude law for pseudodynamic test on small scale reinforced concrete models[J]. Engineering Structures, 2009, 31(4):834-846.
[ 6 ] Ioannis V, Kalpakidis, Micheal C, Constaninou. Principles of scaling and similarity for testing of lead-rubber bearings[J]. Earthquake Engineering and Structural Dynamics, 2010, 39:1551-1568.
[ 7 ] 陈以一,张大照,薛伟辰,等.环向空间预应力结构模型振动台试验研究[J].地震工程与工程振动, 2006,26(6):158-163.
Chen Yiyi, Zhang Dazhao, Xue Weichen, et al. Shaking table model test for circular spatial and prestressed structure[J]. Earthquake Engineering and Engineering Vibration, 2006, 26(6):158-163. (in Chinese)
[ 8 ] 胡锡勇,卢文胜,沈伟明.预应力混凝土简支梁小比例结构模型相似关系[J].结构工程师,2011,27(1):110-117.
Hu Xiyong, Lu Wensheng, Shen Weiming. Similarity law for small-sized model of prestressed concrete simply supported beams[J]. Structural Engineers, 2011, 27(1):110-117. (in Chinese)
[ 9 ] 周颖,卢文胜,吕西林.模拟地震振动台模型实用设计方法[J].结构工程师,2003,19(3):30-33.
Zhou Ying, Lu Wensheng, Lu Xilin. Practical model design method of shaking table tests[J]. Structural Engineers, 2003, 19(3): 30-33. (in Chinese)
[10] 程东辉,薛志成.预应力混凝土结构[M].北京:中国计量出版社,2010.
Cheng Donghui, Xue Zhicheng. Prestressed concrete sturctures[M]. Beijing: China Metrology Publishing House, 2010. (in Chinese)
