基于扩展有限元法的RC剪力墙抗震性能模拟

瓮文芳 余江滔 陆洲导 张远淼

1 引 言

地震作用下的钢筋混凝土结构的力学反应复杂，研究者一般通过低周反复荷载试验对结构构件的抗震性能进行研究。钢筋混凝土构件的抗震性能主要表现在强度[5]刚度退化，耗能能力变化，滞回曲线捏拢等。许多学者在试验的基础上进行大量数值模拟[1-6]，试图通过模拟的方式，将混凝土开裂过程、破坏机理理论化，探究影响构件滞回性能、承载能力、延性等抗震性能的因素。其中大多数的数值模拟是基于有限元法。有限元法采用连续函数作为形函数，求解连续介质的连续变形时非常有效，但在模拟材料断裂方面有着不可克服的困难。混凝土作为弹脆性材料，开裂后反复荷载下会出现裂缝闭合的现象，若仍采用常规有限元法(CFEM)虽具有一定精度，但细观上难以反映混凝土损伤机理，因此引入扩展有限元法。

扩展有限元法[7,8](Extended Finite Element Method，XFEM)是美国西北大学Belytschko教授为代表的研究组于1999年提出的一种数值方法，是基于单位分解的方法(PUM)对单元的形函数加以改进，从而考虑所研究问题的不连续性、奇异性和边界层等特性。它除继承了常规有限元法(CFEM)的优点外，所使用的网格与结构内部的几何或物理界面无关，从而克服了诸如裂纹尖端高应力和变形集中区进行高密度网格剖分所带来的困难，模拟裂纹生长时也无须对网格进行重新剖分。

一些学者已经开始利用XFEM模拟构件开裂过程。方修君等[9]基于ABAQUS平台子程序UEL开发了XFEM程序，利用黏聚性裂纹模型描述混凝土的非线性开裂[10]，模拟印度的Koyna坝的地震开裂过程。霍中艳等[11]在XFEM的基础上，推导了考虑裂尖加强的黏聚性裂缝扩展有限元法，并用这种算法模拟混凝土简支梁集中荷载作用下的开裂过程。杨涛等[12]基于XFEM分别采用三维实体单元和杆单元模拟混凝土和钢筋，采用非线性弹簧单元模拟钢筋混凝土之间的粘结滑移，预设裂缝，模拟简支梁的开裂过程。尹冠生等[13]利用XFEM对混凝土板与梁的损伤进行模拟。

本文采用ABAQUS基于扩展有限元模型对RC剪力墙低周反复荷载作用下的开裂破坏过程模拟，用平面应力单元(plane stress element)模拟混凝土，二力杆单元(truss element)模拟纵向钢筋及箍筋，连接单元(connector element)模拟混凝土与钢筋的粘结-滑移关系。对比低周反复模拟结果与试验结果，包括裂缝开展、承载能力、位移延性和耗能能力等抗震性能，验证了XFEM模拟的可靠性。然后利用该模型计算分析轴压比、剪跨比对RC剪力墙承载力与极限位移的影响。

2 剪力墙设计与试验

试验按照《混凝土结构设计规范》(GB 50010—2010)[14]与《建筑抗震试验方法规程》(JGJ 10—96)[15]制作了2个缩尺RC剪力墙模型，缩尺比例为1/2，分别命名为JLQ1、JLQ2。试件尺寸与配筋如图1所示，配筋数量与试验参数如表1所示，其他具体情况详见文献[15,16]。

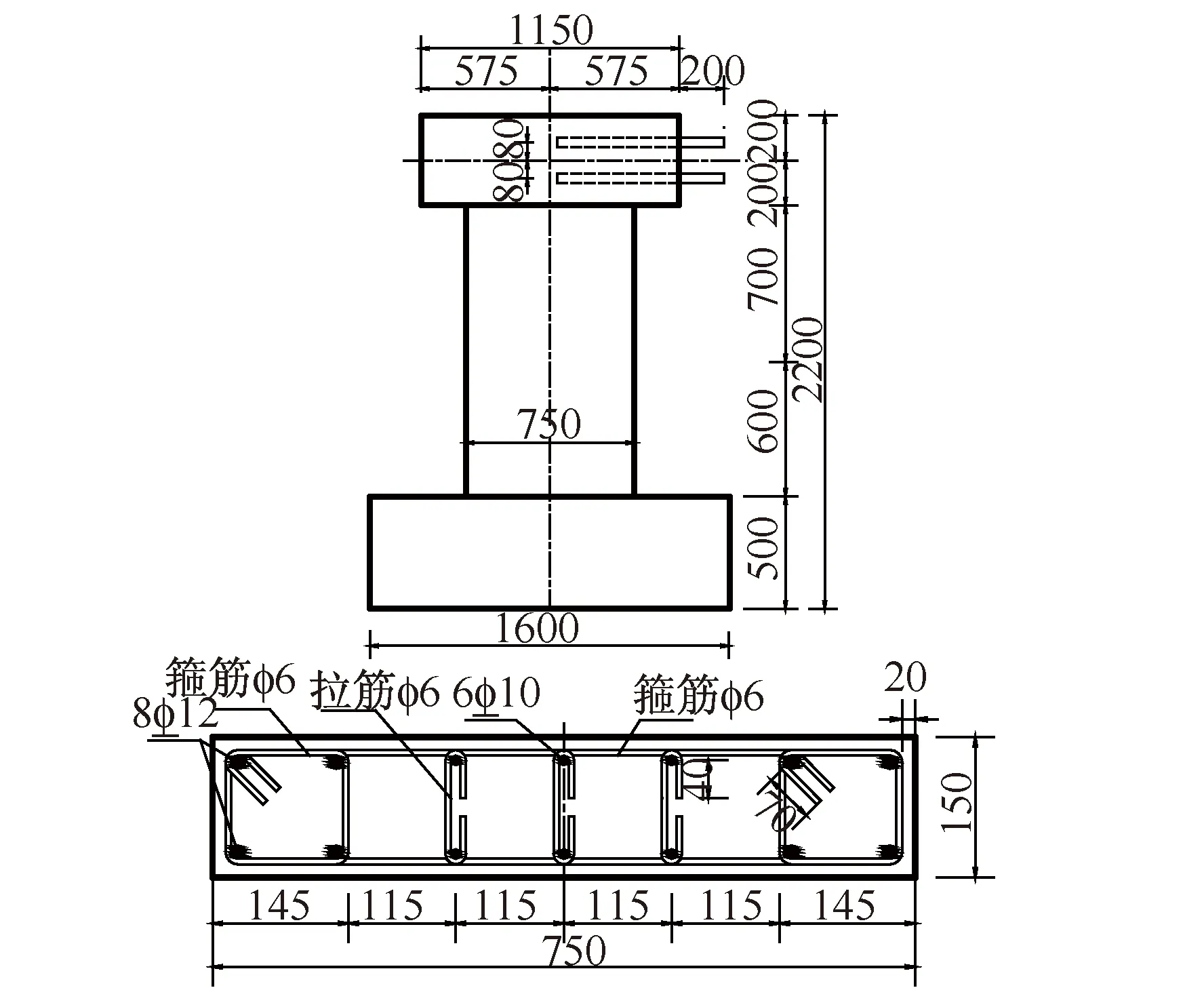
图1 剪力墙尺寸及配筋示意图Fig.1 Details of the general geometry, element section and corresponding reinforcement of shear walls

表1剪力墙参数表

Table1Keyparametersofshearwalls

编号尺寸/mm暗柱纵筋纵筋配筋率全截面纵筋竖向分布筋配筋率箍筋/暗柱箍筋箍筋配筋率水平分布筋分布筋配箍率轴力/kN(轴压比)JLQ1150×750×1 5008 122.086 101.22% 6@1000.77% 6@1000.37%480/0.3JLQ2150×750×1 5008 122.086 101.22% 6@1000.77% 6@1000.37%960/0.6

试件所用混凝土采用C30商品混凝土。混凝土为细石混凝土，配合比为水泥∶沙子∶细石∶水=1∶1.55∶3.61∶0.51。水泥为425#普通硅酸盐水泥，沙子为细沙，细石最大粒径为10 mm，水是普通自来水。通过混凝土轴心受压试验测得所用混凝土棱柱体抗压强度平均值为40.1 MPa，弹性模量为30 244 MPa。所用钢筋力学性能见表2：直径φ6的钢筋为HPB235级圆钢，试件中φ10，φ12，φ18均为HRB335级螺纹钢。

试验加载根据《建筑抗震试验方法规程》(JGJ 101—96)[15]规定进行，先施加竖向荷载到预定值，再施加水平荷载。水平加载采用荷载变形混合控制的加载制度，在试件屈服前采用荷载控制，在试件屈服后采用位移控制。试验过程详见文献[16,17]。

表2钢筋力学性能

Table2MechanicalpropertyofsteelbarsMPa

钢筋直径 6 10 12 18屈服强度354420419385极限抗拉强度456546596559

3 数值模拟参数取值

本文采用ABAQUS有限元分析软件建立剪力墙的有限元模型，具体步骤如下：在Part模块创建部件；在Property模块定义材料性质；在Assembly模块创建实体；在Mesh模块划分网格，再定义网格单元；在Step模块创建两个分析步，分别用于施加竖向轴力与反复水平作用；在Interaction模块中定义各种约束、耦合，包括Connector、XFEM等；在Load模块中定义模型的荷载和边界条件，将底部完全固定，在顶梁中部施加反复的位移荷载，加载制度与荷载大小与试验相同；在Job中提交分析；在Visualization模块中查看模型的分析计算结果并提取所需要的数据。

模型采用XFEM算法来体现混凝土开裂的非连续力学性能。这一模型有别于其他基于连续性介质假定的混凝土模型，分析过程中混凝土的裂纹发生与发展都以虚拟节点[18](phantom node)的生成和分离体现。混凝土基于损伤力学的traction-separation law来建立裂纹的演化过程，包括裂纹的生成(initiation)、裂纹发展(propagation)和裂纹面的分离(separating)三个部分。混凝土的正向受拉破坏为Ι形断裂为主，采用XFEM来模拟Ι形裂纹的出现与扩展可以实现破坏的局部化。因此，本文提出的模型不需要定义混凝土的受拉应力-应变曲线，混凝土的受拉上升段视为线弹性，由输入的弹性模量及最大周向强度因子决定。应力达到指定的周向强度后，判断裂纹生成，裂纹面之间的残余拉力由能量释放率决定。本文以BK混合模式定义基于能量的指数形式(Exponential)损伤演化过程。

图2 粘结—滑移关系曲线Fig.2 Bound-slip curve

4 数值模拟结果

将模拟结果与试验所得结果对比，比较开裂与破坏、滞回曲线与滞回环和骨架曲线，以验证ABAQUS扩展有限元对RC剪力墙抗震性能模拟的可行性。

4.1 开裂与破坏现象对比

试验加载至破坏过程中，试件底部首先出现水平受拉裂缝。水平裂缝出现后，边缘构件中部开始出现斜裂缝。斜裂缝分为两种，一种是剪力墙边缘的主拉应力裂缝，另一种是裂缝源于腹板中部，然后向边缘发展。最终，JLQ1、JLQ2均以底部混凝土被压碎，底部钢筋压弯破坏告终。

数值模拟裂缝结果与前面试验现象较为符合，第一条水平裂缝出现的位置和随后的开展形态与试验现象基本一致。模拟的应力显示最大位移时，主裂缝处钢筋应变达到很大值，受压侧混凝土压应变也达到相当大的程度，这与试验中观察到的外侧钢筋压弯及受压侧混凝土压碎的现象相符合，如图3所示。其中图3(a)、图3(b)为最终破坏图，图3(c)为模拟第一条裂缝开裂情况，图3(d)为模拟最终破坏图。

4.2 混凝土开裂单元的力学反应

传统的有限元计算中，混凝土常常被假定为均匀的连续介质，它的变形特性用宏观应力-应变曲线形式描述，然后再提出本构关系来模拟这些曲线[20]。在近乎线弹性的强化阶段，这一假定是合理的，但在材料受压与受拉的软化阶段，这一假定存在很大的问题。大量的研究证明混凝土的受压与受拉破坏实际上源于局部破坏，局部破坏发生后，通过得到的位移而转化的应变只是整个测量范围内的平均值，不能反映局部应变的变化[21,22]。

图3 试验与模拟结果Fig.3 Results of experiment and simulation

下面基于底部边缘区的混凝土开裂单元的力学反应，从开裂混凝土单元的角度浅析生成的滞回曲线。

如前文所述，开裂是一个位移非连续的过程。通过XFEM的计算，本模型中开裂表现为位移场在不连续单元处的跳跃，以虚拟节点之间的分离体现出来，如图4所示。开裂后，单元会被增加的虚拟节点切断。现将被切断的开裂单元取出，提取其Y方向的应力-应变曲线，如图5所示。图5与我们所熟悉的、传统意义上的混凝土的应力-应变的滞回曲线有很大差别[23,24]。曲线可以认为由受压加载、受压卸载、受拉加载和受拉卸载四部分组成。对于混凝土的受压损伤，本文采用各项同性强化准则(Isotropic Hardening Rule)的塑性模型(Plasticity Model)，因此受压加载、受压卸载与塑性材料无异。值得注意的是，受拉加载和受拉卸载是以线性的方式表现出来的。其物理意义是，混凝土达到最大周向拉应力后，裂纹生成，开裂单元的应力释放，应变以原有的弹性模量的幅度回弹。相比连续介质单元模拟中应变不断增大来反映裂缝的开展，这种受拉应变回弹无疑更接近真实情况，因此相对于CFEM，采用XFEM单元可以更好地模拟开裂混凝土的力学性能。

图4 开裂单元开口Fig.4 Mouth opening of cracking elements

4.3 滞回曲线比较

图5为试件JLQ1、JLQ2的模拟滞回曲线与试验滞回曲线，通过滞回曲线的对比(见图6)可知：

(1) ABAQUS模拟滞回曲线反映的刚度退化、耗能能力等均与试验所得吻合较好，模型可以较好地模拟低周反复荷载作用下剪力墙的抗震性能。

(2) 滞回曲线对比图中，JLQ1(轴压比为0.3)滞回曲线较JLQ2(轴压比为0.6)滞回曲线饱满，表明用该方法模拟轴压比的变化对剪力墙抗震性能产生的影响，与试验对比结论一致。

图7为水平加载峰值位移为20 mm时的模拟滞回环与试验滞回环的对比，模拟结果JLQ2滞回环较JLQ1倾斜斜率增大，即构件刚度明显增大，这与试验所得的滞回环变化一致，表明ABAQUS模型可以很好地模拟出轴压比变化对单个滞回环刚度的影响。

图5 开裂混凝土的应力-应变滞回曲线Fig.5 Stress-strain hysteretic curves of cracked concrete

4.4 骨架曲线对比

力—位移滞回曲线中滞回环峰值点连线得到试件的骨架曲线。如图8所示，通过骨架曲线对比，模拟骨架曲线与试验所得骨架曲线基本重合，表明ABAQUS扩展有限元模型可以近乎精确地模拟出荷载与水平加载位移之间的关系。另外，JLQ2模拟得到的极限承载力明显高于JLQ1，而极限位移相比较小，与试验结果一致，又表明XFEM方法可以很好地模拟承载力与极限位移受轴压比变化的影响。

图6 滞回曲线对比Fig.6 Comparison of hysteretic curves

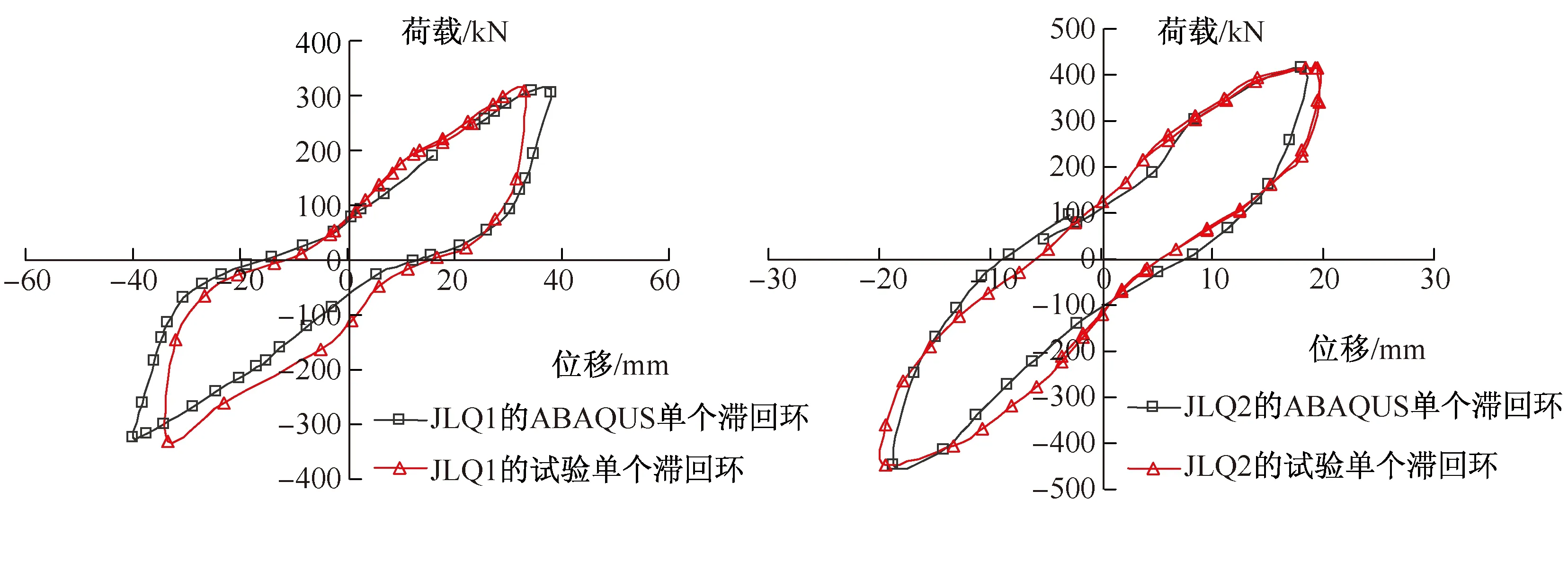
图7 水平位移20 mm滞回环对比Fig.7 Comparison of hysteretic loops at 20 mm lateral displacement

图8 骨架曲线对比Fig.8 Comparison of skeleton curves

JLQ1、JLQ2模拟结果以滞回曲线、单个滞回环、骨架曲线的形式直观对比，将模拟和试验所得的峰值荷载与位移总结如表3所示。由表中数据可知，峰值荷载最大误差为3.39%，峰值位移最大误差为6.67%，模拟结果与试验结果吻合较好，证明采用XFEM模拟低周反复荷载试验是可行的。由以上对比结果可知，采用ABAQUS基于扩展有限元方法对RC剪力墙承载力计算与试验结果吻合较好。

表3模拟结果与试验结果对比表

Table3Comparisonofresultsofexperimentandsimulation

剪力墙峰值荷载试验值/kN模拟值/kN误差峰值位移试验值/mm模拟值/mm误差JLQ1314.3325.03.39%37.540.06.67%JLQ2436.3447.32.52%21.119.8-6.42%

5 参数分析

采用XFEM模型对影响构件的参数轴压比和剪跨比进行有限元分析。

5.1 轴压比

模拟中采用11组不同的轴压比，为了确定RC构件合适的轴压比范围，平均取0.1～1.0之间10个数进行单向的水平加载模拟，并设置轴压比为0的对照组。模拟计算的结果如表4及图9所示。

图9 不同轴压比下的极限位移对比Fig.9 Comparison of one-dimensional displacements with different axial compression ratios

表4不同轴压比下峰值荷载的对比

Table4Comparisonofpeakloadwithdifferentaxialcompressionratio

轴压比峰值荷载/kN轴压比峰值荷载/kN轴压比峰值荷载/kN0232.60.4387.50.8443.40.1285.10.5390.00.9455.50.2281.40.6421.51.0455.10.3334.80.7432.4

由上述计算结果可知：轴压比小于0.6时，RC剪力墙承载力随着轴压比的增大而增大，且增大幅度比较明显；当轴压比大于0.6时，随着轴压比的增大，剪力墙承载力提高幅度明显变小。轴压比增大对承载能力提升的原因可能是其延缓和限制了裂缝的开展，从而减小裂缝间钢筋的拉应力；在轴压比增大到一定程度后对承载力提高幅度减小的原因可能是过大的轴压比增大了受压区混凝土的压应力从而抑制了承载力的提高。

当轴压比为0.1～0.3时，由于轴压比较小，对极限位移几乎没有影响；而轴压比大于0.3小于0.5时，轴压比的增大使剪力墙的刚度增大，延性稍有减小；轴压比大于0.5之后，延性急剧减小。

就承载力而言，轴压比为0～0.6时，对剪力墙承载力有所提升，轴压比取值越大越好；就延性而言，轴压比取0～0.5比较合适，再增大就会造成延性的显著下降。综合考虑剪力墙承载力与位移延性影响，建议剪力墙轴压比取值为0.5左右较合适。

5.2 剪跨比

试验中剪力墙的剪跨比均为2，为更深入了解剪跨比对构件承载力的影响，模拟中采取了8组不同的剪跨比，进行单向的水平加载模拟。模拟的结果如表5及图10所示。

表5不同剪跨比下峰值荷载的对比

Table5Comparisonofpeakloadwithdifferentshearspanratio

剪跨比峰值荷载/kN剪跨比峰值荷载/kN0.61 2611.35480.7410271.54900.879051.753861.16832335

由上述计算结果可知：RC剪力墙承载力随着剪跨比的减小而增大，且承载力增大比较明显，当剪跨比小于1.0之后，随着剪跨比的减小，剪力墙承载力提高幅度明显变大；构件极限位移随着剪跨比的减小而减小。

剪跨比对墙体承载能力的提高作用可能是因为：剪跨比减小会减小水平推力引起的墙体底部的弯矩，从而抑制了水平裂缝的开展，这不仅对墙体抗弯能力有提升，对墙体的抗剪能力也有帮助。剪跨比较小时墙体的受力形式类似于深梁，其抵抗水平推力的能力强于剪跨比较大的墙体。

图10 不同剪跨比下的单向位移对比Fig.10 Comparison of one-dimensional displacements with different shear span ratios

6 结 论

本文通过试验与模拟的对比和ABAQUS扩展有限元进一步分析，可以得到以下结论：

(1) 采用基于XFEM的ABAQUS模型可以模拟混凝土开裂后的不连续性，通过计算结果与试验结果对比，表明扩展有限元方法能够有效模拟RC剪力墙裂缝开展后的力学性能和轴压比变化对其产生的影响，具有较好的精度。

(2) XFEM法所得的单元滞回曲线有别于宏观滞回曲线，它将混凝土破坏归结为局部破坏，考虑了开裂后混凝土的受拉回弹，更接近真实情况，结果更加可靠。因此可以对单元滞回曲线对整体抗震性能的影响作进一步探究。

(3) RC剪力墙的承载力随轴压比的增大而增大，极限位移随之减小；轴压比大于0.6时，由于同时增大了受压区的压力而抑制构件承载力的增加。为了获得较好的抗震性能，RC剪力墙设计时应考虑将轴压比的大小限制在一定的范围内。

(4) 剪跨比对RC剪力墙的承载力也有较大的影响。剪跨比小的RC剪力墙破坏形式类似于深梁，随剪跨比减小，承载力增大，极限位移减小，延性降低。因此，实际工程设计中，应将剪跨比也作为一项重要的影响因素加以考虑。

[ 1 ] 韩小雷,陈学伟,吴培峰,等.OpenSEES的剪力墙宏观单元的研究[J].世界地震工程,2008,24(4):76-82.

Han Xiaolei, Chen Xuewei, Wu Peifeng, et al. Research on the shear wan macro-element of Open SEES [J]. World Earthquake Engineering, 2008, 24(4): 76-82.(in Chinese)

[ 2 ] 韩小雷，陈学伟,戴金花,等.基于OpenSEES的剪力墙低周往复试验的数值分析[J].华南理工大学学报(自然科学版),2008, 36(12):8-16.

Han Xiaolei, Chen Xuewei, Dai Jinhua, et al. Numerical analysis for low-cyclic loading test of shear walls based on Open SEES [J]. Journal of South China University of Technology (Natural Science Edition), 2008(12), 36(12): 8-16.(in Chinese)

[ 3 ] 韩向科,张晓明.T形型钢混凝土短肢剪力墙承载力模拟分析[J].山西建筑，2007,33(23):61-62.

Han Xiangke, Zhang Xiaoming. Simulation analysis of bearing capacity of short-leg T-shaped steel reinforced concrete shear wall [J]. Shanxi Architecture, 2007, 33(23): 61-62.(in Chinese)

[ 4 ] 吕西林，卢文生.纤维墙单元模型在剪力墙结构非线性分析中的应用[J].力学季刊,2005(3), 26(1):72-80.

Lu Xilin, Lu Wensheng. Application of element model non-linear analysis of shear wall structures[J]. Chinese Quarterly Mechanics, 2005(3), 26(1): 72-80.(in Chinese)

[ 5 ] 杨溥，唐剑，陈名弟,等.钢筋混凝土异形柱在不同加载方向的受力性能分析[J].重庆大学学报(自然科学版),2005,28(8):117-121.

Yang Pu, Tang Jian, Chen Mingdi, et al. Analysis on seismic capacity for RC specially shaped columns in different horizontal direction[J]. Journal of Chongqing University(Natural Science Edition), 2005, 28(8): 117-121.(in Chinese)

[ 6 ] 王琨，袁沈峰，郑文忠.水平荷载作用下型钢混凝土梁-角钢混凝土柱框架非线性有限元模拟[J].结构工程师,2011,27(6):41-47.

Wang Kun, Yuan Shenfeng, Zheng Wenzhong. Nonlinear finite element simulation on a frame structure of steel reinforced concrete beam and angle steel concrete column under horizontal loading[J]. Structural Engineers, 2011, 27(6): 41-47.(in Chinese)

[ 7 ] Belytschko T, Black T. Elastic crack growth in finite elements with minimal remeshing[J]. International Journal for Numerical Methods in Engineering, 1999, 45(5): 601-620.

[ 8 ] Mo⊇s N, Dolbow J, Belytschko T. A finite element method for crack growth without remeshing[J]. International Journal for Numerical Methods in Engineering, 1999, 46(1): 131-150.

[ 9 ] 方修君，金峰，王进廷.基于扩展有限元法的Koyna重力坝地震开裂过程模拟[J].清华大学学报(自然科学版)，2008,48(12)：2065-2069.

Fang Xiujun, Jin Feng, Wang Jinting. Seismic fracture simulation of the Koyna gravity dam using an extended finite element method [J]. Tsinghua Univ (Science and Technology), 2008, 48(12): 2065-2069.(in Chinese)

[10] 方修君,金峰,王进廷.用扩展有限元方法模拟混凝土的复合型开裂过程[J].工程力学,2007, 24(S1):46-52.

Fang Xiujun, Jin Feng, Wang Jinting. Simulation of mixed-mode fracture of concrete using extended finite element method [J]. Engineering Mechanics, 2007, 24(S1): 46-52.(in Chinese)

[11] 霍中艳，郑东健.基于XFEM的黏聚性裂缝模型模拟混凝土开裂过程[C].中国计算力学大会2010(CCCM2010暨第八届南方计算力学学术会议(SCCM8)论文集,2010.

Huo Zhongyan, Zheng Dongjian. Simulation of concrete cracking using cohesive crack model based on XFEM [C]. Proceedings of the 2010 Chinese Congress on Computational Mechanics in conjunction with the 8th South Congress on Computational Mechanics, 2010.(in Chinese)

[12] 杨涛，邹道勤.基于XFEM的钢筋混凝土梁开裂数值模拟[J].浙江大学学报(工学版),2013,47(3)：495.

Yang Tao, Zou Daoqin. Numerical simulation of crack growth of reinforced concrete beam based on XFEM[J]. Journal of Zhejiang University (Engineering Science),2013, 47(3): 495.(in Chinese)

[13] 尹冠生,周肖飞.基于XFEM的损伤扩展模拟[J].长安大学学报(自然科学版),2013,33(2):68-72.

Yin Guansheng, Zhou Xiaofei. Crack propagation simulation based on extended finite element method [J].Journal of Chang’an University (Natural Science Edition),2013, 33(2), 68-72.(in Chinese)

[14] 中华人民共和国住房和城市建设部.GB 50010—2010混凝土结构设计规范[S]. 北京：中国建筑工业出版社，2010.

Ministry Housing and Urban-Rural of Construction of the People’s Republic of China.GB 50010—2010 Code for design of concrete structures [S]. Beijing: China Architecture and Building Industry Press, 2010.(in Chinese)

[15] 中华人民共和国住房和城市建设部.JGJ 101—96建筑抗震试验方法规程[S].北京：中国建筑工业出版社，1997.

Ministry of Construction of the People’s Republic of China.JGJ 101—96 Specification of testing methods for earthquake resistant building[S]. Beijing: China building Architecture and Press, 2010.(in Chinese)

[16] 唐波.“一”字形扁柱、短肢剪力墙拟静力试验研究[D].上海：同济大学，2012.

Tang Bo. Pseudo-static experimental researches on flat column with shallow rectangular section and short-pier shear wall [D].Shanghai: Tongji University, 2012.(in Chinese)

[17] 魏亮亮.水平推力作用下短肢剪力墙的试验和数值模拟研究[D].上海：同济大学,2013.

Wei Liangliang. Experimental researches and numerical analysis of short-pier shear wall under horizontal thrust [D]. Shanghai: Tongji University, 2013.(in Chinese)

[18] Song J H, Areias PMA, Belytschko T. A method for dynamic crack and shear band propagation with phantom nodes [J]. International Journal for Numerical Methods in Engineering, 2006, 67(6): 868-893.

[19] CEB-FIP Model Code.Design code[S].1990.

[20] 陈惠发.弹性与塑性力学[M].北京：中国建筑工业出版社,2005:276.

Chen Huifa. Elasticity and plasticity [M]. Beijing: China Architecture and Building Press,2005: 276.(in Chinese)

[21] Van Mier J G M. Complete stress-strain behavior and damaging status of concrete under multi-axial conditions [C]. International Conference on Concrete under Multi-axial Conditions, Pressesdel’ University’s Paul Sabatier, Toulouse, France,1984(1): 124-132.

[22] Korsovos M D. Effect of testing techniques on the post-ultimate behavior of concrete in compression [J]. Material and Structures (RILEM), 1983,16(91): 3-12.

[23] Lee J, Fenves G. Plastic-damage model for cyclic loading of concrete structures [J]. Engineering Mechanics. (1998), 124(8), 892-900.

[24] Sakai J, Kawashima. Unloading and reloading stress-strain model for confined concrete [J]. Structure Engineering, 2006, 132(1), 112-122.