大跨度公铁两用斜拉桥列车制动力作用下结构响应研究

吕 龙 李建中

1 引 言

随着桥梁跨径不断增加，斜拉桥不断涌现，斜拉桥常常受地震、风、列车制动力等动力荷载控制，斜拉桥结构体系对结构动力反应有显著的影响[1]。合理设计塔梁连接方式是控制斜拉桥在地震、列车荷载作用下结构动力反应的关键。在塔梁间设置弹性约束装置和阻尼约束装置是两种常用措施。塔梁间增加弹性约束装置能有效降低主梁纵向位移，但没有耗能作用，增大结构受力。塔梁之间采用纵向阻尼约束装置，通过额外增加的阻尼起到耗能作用，改变结构局部构件传力关系，调整结构动力响应，能有效控制主梁纵向位移。在大跨度斜拉桥中，黏滞阻尼器是一种应用较多的阻尼约束装置。

国内外学者对斜拉桥塔梁间合理选择阻尼参数进行了一些研究，并应用于实际桥梁[2-6]。但在进行阻尼器参数合理选取时，大多数是对地震荷载作用下结构响应进行研究，设置阻尼器列车制动力对桥梁结构响应影响的研究尚属空白。随着高铁快速发展，大跨度铁路斜拉桥不断应用于铁路建设中，因此对这方面的研究很有必要。本文主要研究了设置阻尼器后，公铁两用斜拉桥在列车制动力作用下桥梁结构动力响应，并与未设置阻尼器情况下结构动力响应相比较。

2 大吨位黏滞阻尼器工作原理

大吨位黏滞阻尼器由活塞、油缸和阻尼孔组成。其原理是利用活塞前后压力差使油流过阻尼孔产生阻尼力。阻尼器阻尼力与相对速度有关，表达式为

F=CVα

(1)

式中，F为阻尼力，kN；C为阻尼常数，kN/(m·s-1)α，与阻尼孔开孔面积有关；V为阻尼器相对速度，m/s；α为速度指数(其值应用范围一般为0.2～1.0)，当α=1，即阻尼力与相对速度成比例时，称为线性阻尼器，当α≠1，即阻尼力与相对速度不成比例时，称为非线性阻尼器。

由式(1)可知，当速度指数α为定值，阻尼力F随阻尼常数C增大而增大；对于α<1时，当阻尼常数为定值时，阻尼力F与速度指数α的关系和阻尼器相对速度V有关，当V<1 m/s时，阻尼力F随速度指数α增大而减小，当V>1 m/s 时，则相反[2]。

图1给出了不同参数的黏滞阻尼器模型滞回曲线。当α=1时，滞回曲线近似为椭圆，滞回曲线随α的减小逐渐接近于矩形。当阻尼器阻尼力最大时，其相对位移最小，相对速度大；当阻尼器相对位移最大时，其相对速度小，因而阻尼力最小，接近于零。

图1 黏滞阻尼器滞回曲线Fig.1 Hysteretic curve of viscous damper

3 计算模型

某大跨度公铁两用斜拉桥为主跨1 092 m的双塔三索面平弦钢桁梁斜拉桥(图2)，桥跨组合为140 m+462 m+1 092 m+462 m+140 m，上层为六车道公路，下层为四线铁路。主梁采用箱桁组合桁架结构，桁架下弦由与主梁断面同宽的钢箱组成，钢箱同时兼作整体桥面。主梁桁高16 m，桁宽35 m。边跨侧224 m 范围公路桥面采用带有混凝土桥面板的结合截面。主塔为钻石形钢筋混凝土桥塔，塔高325 m。每个主塔和桥墩在每片主桁下均设纵向活动支座，两主塔处主塔横梁和主桁之间分别设置6个液体黏滞阻尼器。

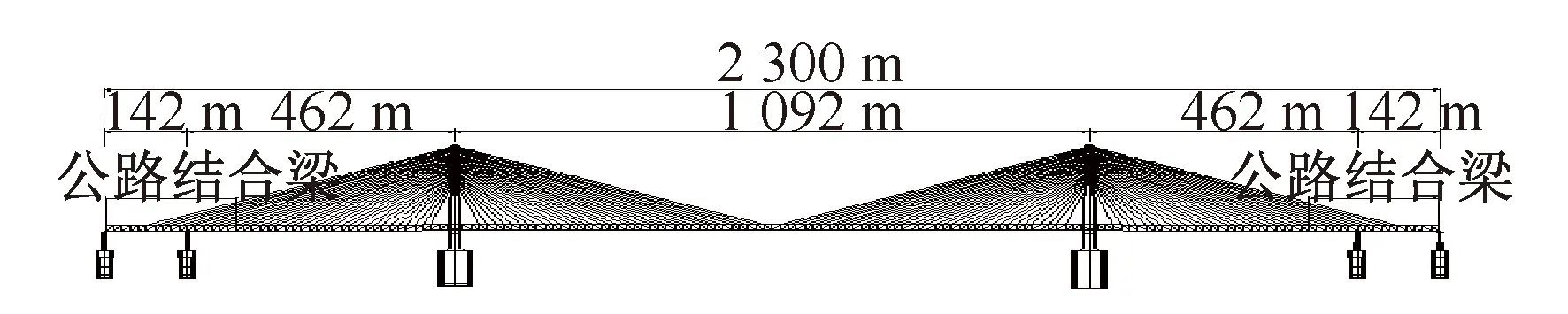
图2 总体布置图Fig.2 General arrangement plan

本文采用SAP2000建立桥梁结构有限元模型，分析结构动力特性和动力响应[7]。主桥钢桁梁用三维桁架单元模拟；主塔和墩用三维梁单元模拟，考虑恒载轴力引起的几何刚度的影响；斜拉索采用三维梁单元模拟，释放模拟拉索的梁单元两端抗弯、抗扭自由度，考虑斜拉索垂度效应及恒载引起的几何刚度的影响，采用Ernst公式修正拉索弹性模量考虑垂度效应；通过在承台质心处施加集中质量模拟承台的作用。

4 制动力计算模型

对于列车制动力国内外学者做了较多研究[8-10]，列车制动力主要来自轮轨之间的滚动摩擦，即：

T=μW

(2)

式中，T为列车制动力；μ为轮轨摩擦系数；W为所考虑范围内列车重力，文中取一线ZK活载和一线中-活载的列车重量为7 662 t。

活载加载图示如图3所示。

由式(2)得到列车减加速度与轮轨摩擦系数之间关系：

μ=T/W=a/g

(3)

式中，a为列车减加速度。

由上述关系，参考秦沈线实测列车减加速度变化曲线，列车减加速度转化为相应的轮轨摩擦系数，求得列车制动力，图4为秦沈线实测列车减加速度变化曲线及相应简化制动力时程曲线。

图3 活载加载图示Fig.3 Live load loading schema

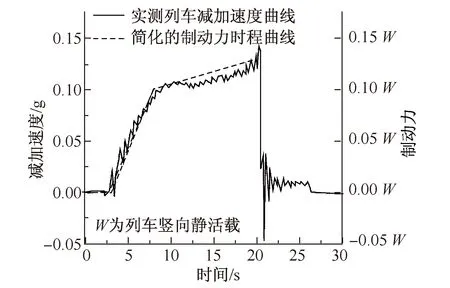
图4 实测列车减加速度及简化制动力曲线Fig.4 Actual train deceleration curve and simplified train braking force curve

由于列车在桥梁上制动时为紧急制动，是为使列车尽快停住而实施的制动，这种情况下的制动力作用比较迅猛，且用上了列车的全部制动能力，而列车制动能力由列车制动装置决定。因此，同一列车以不同行车速度制动时，制动力变化规律相似，仅是列车制动持续时间不同。

由实测列车减加速度变化曲线可知，列车减加速度由0至0.1 g持续时间约为6 s，而0.1 g至最大减加速度所需时间与减加速度峰值大小相关。实测的列车制动减加速度峰值范围为(0.1～0.15) g[3]。本文取减加速度峰值为0.1 g、0.125 g、0.15 g三种情况计算列车制动力。

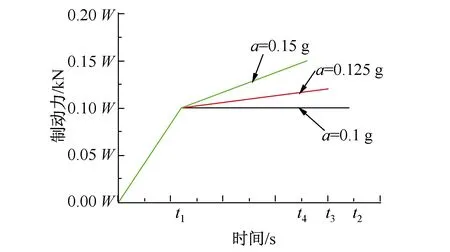
图5 制动力加载时程曲线Fig.5 Braking force loading time-history curve

表1制动力加载时程参数

Table1Parametersforthebrakingforceloadingtime-historycurve

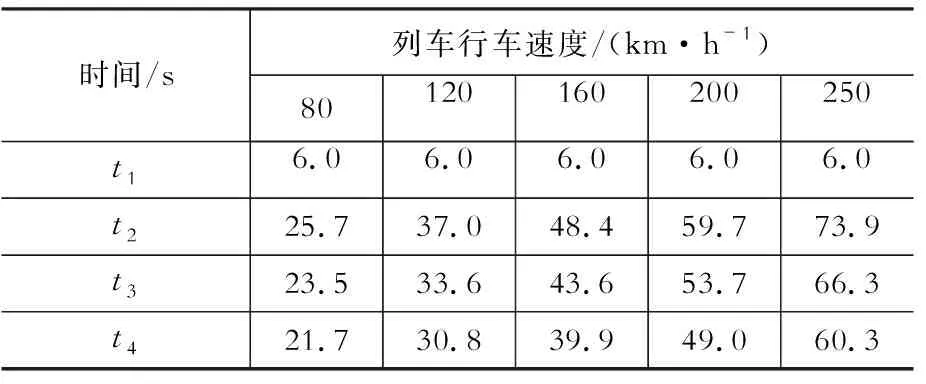
时间/s列车行车速度/(km·h-1)80120160200250t16.06.06.06.06.0t225.737.048.459.773.9t323.533.643.653.766.3t421.730.839.949.060.3

根据运动方程及制动持续时间则可确定不同行车速度制动过程中列车速度变化规律，如图6所示。

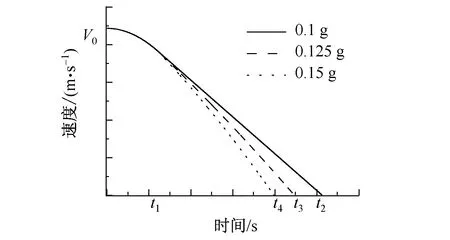
图6 列车制动过程中速度变化曲线Fig.6 Velocity changing in the process of train braking

5 结构动力响应分析

为研究列车制动力对结构动力响应的影响，分别选取单个阻尼器阻尼常数C为0，1 000，3 000，4 500，7 000，10 000，15 000，20 000，25 000共9个值；速度指数α为0.3，0.4，0.5，0.7，1.0共5个值，总计45组参数。计算每组参数在列车行车速度以80 km/h，120 km/h，160 km/h，200 km/h，250 km/h制动时结构的最大动力响应，并取减加速度峰值为0.1 g，0.125 g，0.15 g三种情况下结构响应最大值。其中，C=0为飘浮体系，C≠0为阻尼体系。

列车在制动过程中，由于轮轨与轨道间摩擦作用，使得主梁受到纵桥向水平力作用，而产生纵桥向振动，并引起塔底内力。若桥梁结构为漂浮体系，则导致塔梁间相对位移；若在塔梁间设置阻尼器，则会导致阻尼器产生动力响应，并影响结构在制动力作用下动力响应。

图7给出了列车制动力作用下阻尼参数对塔底剪力的影响。由图可知，塔底剪力受速度指数影响较小，当阻尼常数C<4 500 kN/(m·s-1)α时，塔底剪力随阻尼常数的增大而显著减小；当阻尼常数C>4 500 kN/(m·s-1)α时，塔底剪力受阻尼常数影响较小，保持在3 200 kN左右，行车速度对塔底剪力影响不大。

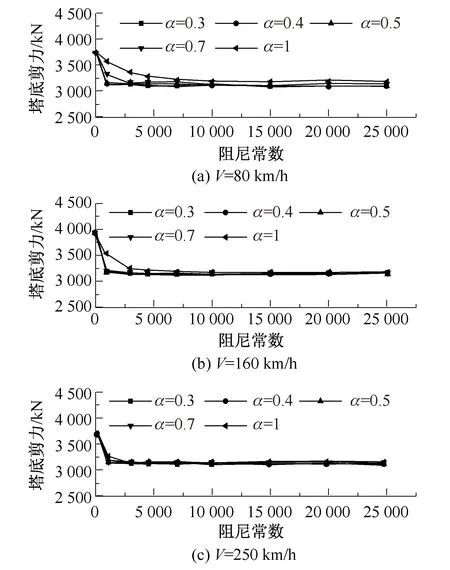
图7 列车制动力作用下阻尼参数对塔底剪力影响Fig.7 Influence of damping parameters on tower bottom shear forces under train braking forces

图8给出了列车制动力作用下阻尼参数对塔底弯矩的影响。图中表明，塔底弯矩随阻尼常数的增大而减小，并趋近于常数；塔底弯矩受速度指数影响较大，并随速度指数增大而增大，在300～1 000 MN范围内变化；行车速度对塔底弯矩有一定的影响，总体上塔底弯矩随行车速度增大而增大，其增幅受阻尼参数影响较大。

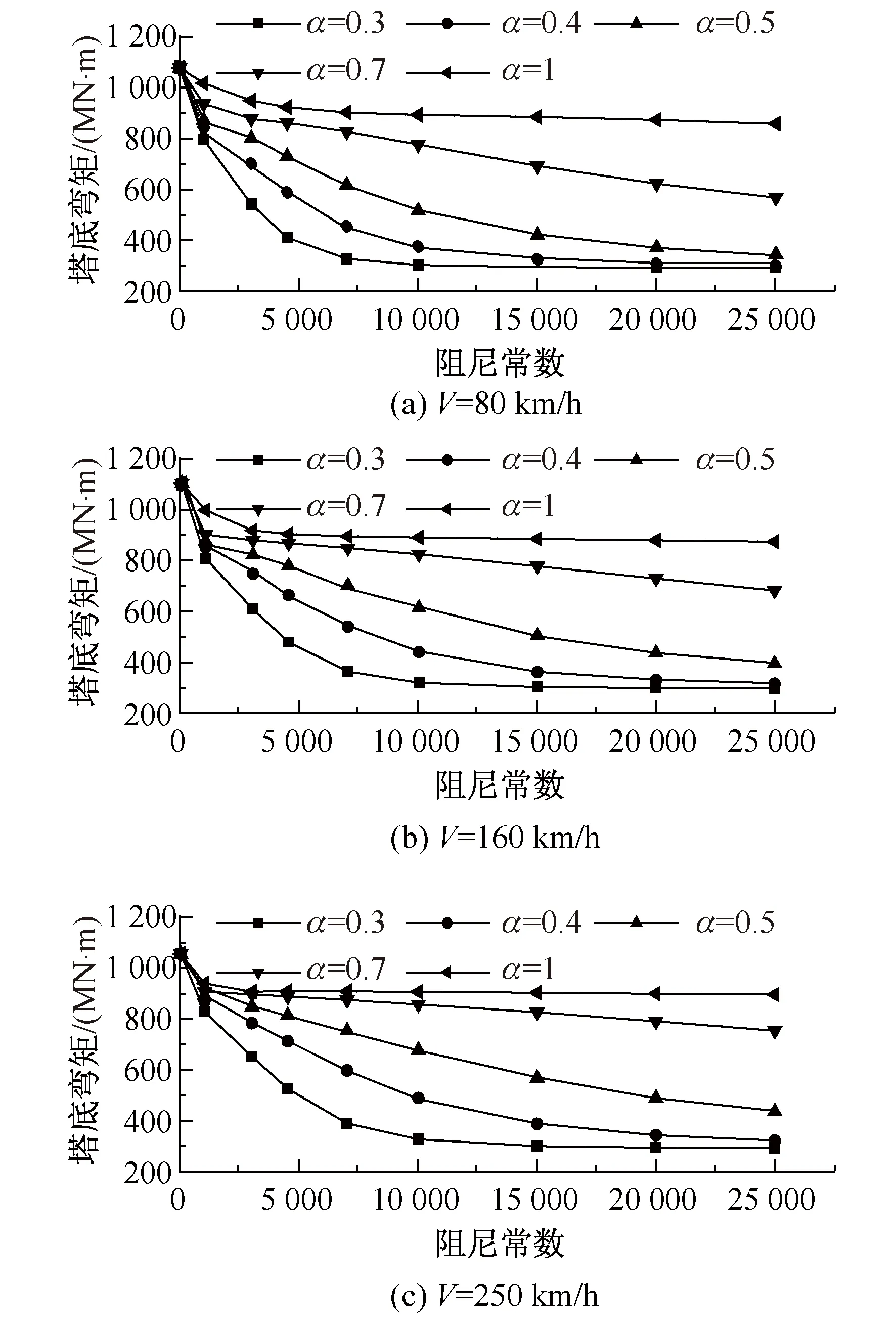
图8 列车制动力作用下阻尼参数对塔底弯矩影响Fig.8 Influence of damping parameters on tower bottom moment under train braking forces

图9给出了列车制动力作用下阻尼参数对梁端位移的影响。从图中可知，梁端位移随阻尼常数的增加快速减小，并趋近于常数；梁端位移受速度指数影响较大，随速度指数增大而增大，在0.01～0.2 m范围内变化；此外，行车速度对梁端位移有一定的影响，总体上梁端位移随行车速度增大而增大，其增幅受阻尼参数影响较大。

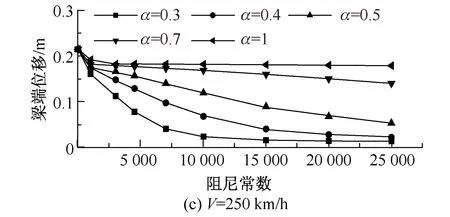
图9 列车制动力作用下阻尼参数对梁端位移影响Fig.9 Influence of damping parameters on displacement of beam end subjected to train braking force

图10给出了列车制动力作用下阻尼参数对塔梁相对位移(阻尼器位移)的影响。由图可知，塔梁相对位移和梁端位移具有相同的变化规律。

图10 列车制动力作用下阻尼参数对塔梁相对位移影响Fig.10 Influence of damping parameters on displacement between tower and beam under train braking forces

图11给出了列车制动力作用下阻尼参数对阻尼器阻尼力的影响。由图可知，阻尼力随阻尼常数增大而增大，并逐渐趋于常数；阻尼力受速度指数影响较大，随速度指数增大而减小，在400～900 kN范围内变化；行车速度对阻尼器阻尼力影响不大。

图11 列车制动力作用下阻尼参数对阻尼力影响Fig.11 Influence of damping parameters on damping forces under train braking forces

综合以上参数分析可知，在塔梁间设置阻尼器能显著减小塔底内力，梁端位移及塔梁间相对位移。当阻尼常数C<10 000 kN/(m·s-1)α时，塔底地震内力及梁端位移随阻尼常数增大而显著减小，且在阻尼常数增大到4 500 kN/(m·s-1)α后，效果更加显著；当阻尼常数C<10 000 kN/(m·s-1)α时，则趋于常数，若继续增大阻尼常数则较C=10 000 kN/(m·s-1)α时无更显著效果。因此，建议阻尼常数采用4 500～10 000 kN/(m·s-1)α。若采用同一阻尼常数，当速度指数较小时，结构地震响应的减小更加显著，而阻尼力更大，但其数值仍较小，因此，建议速度指数α可取0.3。

从表2列出的制动力作用下结构动力响应可知，阻尼体系(C=4 500，α=0.3)塔底内力及梁端位移和塔梁相对位移均小于漂浮体系，其中，对于不同行车速度，塔底剪力减小为漂浮体系的80%～85%，塔底弯矩减小为35%～50%；阻尼体系梁端位移和塔梁相对位移减小为漂浮体系的20%～35%。

表2列车制动力作用下结构响应

Table2Structuralresponsesundertrainbrakingforces

行车速度/(km·h-1)80120160200250阻尼体系塔底剪力/kN3 1133 1163 1493 1453 147塔底弯矩/(MN·m)389449484507531梁端位移/m0.0430.0540.0620.0690.075塔梁相对位移/m0.0370.0480.0560.0620.068漂浮体系塔底剪力/kN3 7453 8653 9433 7443 716塔底弯矩/(MN·m)1 0721 1031 1271 0691 063梁端位移/m0.2110.2200.2240.2120.210塔梁相对位移/m0.2010.2100.2130.2020.200

图12为未设置和设置阻尼器梁端位移时程图，图中表明，设置阻尼器能有效地控制主梁纵向位移。综合表2和图12表明，设置阻尼器对降低结构位移和改善结构受力有利。

图12 列车制动力作用下梁端位移时程图Fig.12 Time-history of beam end displacements under train braking forces

6 结 论

(1) 对于大跨度公铁两用斜拉桥，列车制动力会导致主梁纵向振动及引起塔底弯矩，因此，在选取阻尼器参数时，有必要考虑列车制动力作用下结构及阻尼器动力响应。

(2) 塔梁间设置阻尼器对列车制动力作用下结构动力响应影响较大。合理选择阻尼器参数能有效地减小塔底弯矩、梁端位移及塔梁相对位移，但对塔底剪力影响相对较小。对于本文分析的大跨度公铁两用桥，建议在每个塔梁间设置6个阻尼常数为4 500～10 000 kN/(m·s-1)α，速度指数为0.3的大吨位黏滞阻尼器。

[ 1 ] 叶爱君,胡世德,范立础.斜拉桥抗震结构体系研究[J].桥梁建设, 2002(4):1-4.

Ye Aijun, Hu Shide, Fan Lichu. Research on aseismatic structural system of cable-stayed bridge[J]. Bridge Construction, 2002(4): 1-4. (in Chinese)

[ 2 ] 叶爱君,范立础.附加阻尼器对超大跨度斜拉桥的减震效果[J].同济大学学报(自然科学版),2006, 34(7):859-863.

Ye Aijun, Fan Lichu. Seismic response reduction of a super-long-span cable-stayed bridge by adding dampers[J]. Journal of Tongji University (Natural Science Edition), 2006, 34(7): 859-863. (in Chinese)

[ 3 ] 梁智垚，李建中.大跨度公铁两用斜拉桥阻尼器参数研究[J].同济大学学报(自然科学版), 2007, 35(6):728-733.

Liang Zhiyao, Li Jianzhong. Research on damper parameters of long-span rail-cum-road cable-stayed bridge[J]. Journal of Tongji University (Natural Science Edition), 2007, 35(6): 728-733. (in Chinese)

[ 4 ] 秦顺全.武汉天兴洲公铁两用长江大桥关键技术研究[J].工程力学,2008, 25(12):99-105.

Qin Shunquan. Key technology of Tianxingzhou Yangtze River Brigde [J]. Engineering Mechanics, 2008, 25(12):99-105. (in Chinese)

[ 5 ] 王志强, 胡世德, 范立础.东海大桥黏滞阻尼器参数研究[J].中国公路学报, 2005,18(3):37-421.

Wang Zhiqiang, Hu Shide, Fan Lichu. Research on viscous damper parameters of Donghai Bridge [J]. China Journal of Highway and Transport, 2005, 18(3): 37-421. (in Chinese)

[ 6 ] 韩万水，黄平明，兰燕．斜拉桥纵向设置黏滞阻尼器参数分析[J].地震工程与工程振动,2005, 25(6):146-151.

Han Wanshui, Huang Pingming, Lan Yan. Parametric analysis of cable-stayed bridge with longitudinal viscous dampers [J]. Earhquake Engineering and Engineering Vibration, 2005, 25(6): 146-151. (in Chinese)

[ 7 ] Wilson E L.Three dimensional static and dynamic analysis of structures: A physical approach with emphasis on earthquake engineering [M]. California: Computers and Structures Inc., 2002.

[ 8 ] 王锐锋, 李宏年. 铁路桥梁列车制动力荷载研究[J].北方交通大学学报, 2003, 27(1):63.

Wang Ruifeng, Li Hongnian. Study of train braking force on railroad bridge[J]. Journal of Northern Jiaotong University, 2003, 27(1): 63. (in Chinese)

[ 9 ] 雷俊卿,李宏年,冯东.铁路桥梁列车制动力的试验研究与计算分析 [J].工程力学, 2006, 23(3): 134-140.

Lei Junqing, Li Hongnian, Feng Dong. Expericemengt study and computational analysis on baking force between running train and railway bridge[J]. Engineering Mechanics, 2006, 23(3): 134-140. (in Chinese)

[10] 瞿伟廉,刘嘉,涂建维,等.天兴洲公铁两用斜拉桥主梁纵向列车制动振动反应分析[J].地震工程与工程振动, 2008, 28(1):130-138.

Qu Weilian, Liu Jia, Tu Jianwei, et al. Longitudinal response analysis of Tianxingzhou highway and railway combined cable-stayed bridge subjected to train braking and traffic[J]. Earhquake Engineering and Engineering Vibration, 2008, 28(1): 130-138. (in Chinese)