基坑支护中桩长设置的影响因素分析

林 洁 李科成

1 引 言

钻孔灌注桩在工程支护中已经得到了较好应用，尤其在边坡及基坑支护工程中更是运用广泛。孔德森等[1]研究了倾斜支护桩在基坑中的应用，分析桩体的变形及受力特征，得到的结论为倾斜桩能够更好地发挥桩身材料的强度，其中桩顶位移较直桩有所减小，桩身弯矩分布与直桩也有差别。高广运等[2-4]研究了桩周土体的物理力学性质对灌注桩承载力的影响，主要得出了土体模量对桩承载力影响较大的结论。吴刚等[5-7]研究双排桩在基坑支护中的设计计算方法，主要是应用弹性地基梁法确定桩体参数。在这些研究中，主要分析了灌注桩的设计计算方法，影响灌注桩承载力的因素等。对于在基坑支护中，灌注桩桩长的影响因素少有涉及，因此本文主要针对这一问题进行探讨。

本文以软土基坑支护工程为例，主要分析影响灌注桩桩长设置的因素，如桩周土体的物理力学参数中黏聚力、摩擦角的影响，以及基坑开挖深度的影响。在分析时采用数值软件计算基坑的变形及稳定性，在计算时调整土体的物理力学参数及基坑开挖深度，同时调整灌注桩长度使基坑变形量保持在一定范围内，再结合基坑整体稳定性系数，以此来确定上述因素变化对最佳桩长的影响，并建立相关关系公式，为基坑支护桩的设计提供理论参考。

2 数值模型的建立

本文采用FLAC3D[8-9]软件计算，对这一问题进行分析。背景为一开挖深度为6 m的基坑，支护形式是单排钻孔灌注桩，为柔性悬臂式支护结构。计算时忽略土体分层情况，因此土体为单一土层，基坑工程安全等级为三级，基坑整体稳定性系数不低于1.25，悬臂式支挡结构嵌固稳定安全系数不低于1.15。模拟计算时土体采用摩尔-库伦本构模型，支护结构采用FLAC3D自带的beam单元，初始应力采用计算自动生成。模型长度与高度均为40 m，取基坑一半为计算对象，开挖宽度为20 m。

模拟时取模型厚度为1 m，将计算等效成平面问题，基坑开挖时分为层开挖，开挖一层运行800步，开挖完成时计算至稳定状态。模型底部采用全约束，即约束所有方向的变形，模型侧边约束水平方向的变形，模型顶部为自由面，无约束。土体及支护结构参数见表1，数值模型见图1。

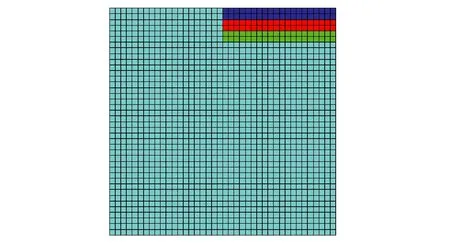
图1 数值模型Fig.1 The numerical model

表1土层及支护结构物理力学参数

Table1Mechanicalparametersofthesoilandthesupportingstructure

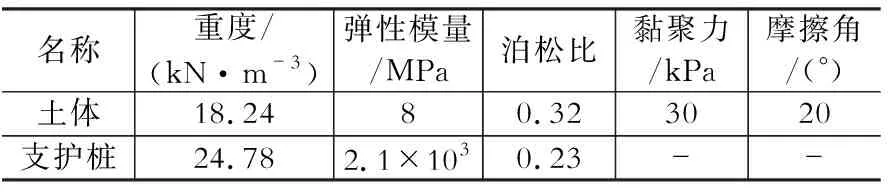
名称重度/(kN·m-3)弹性模量/MPa泊松比黏聚力/kPa摩擦角/(°)土体18.2480.323020支护桩24.782.1×1030.23--

3 计算结果分析

3.1 合理桩长的确定

首先设置不同桩长分别计算开挖土体的位移及稳定性情况，桩长分别为7 m、8 m、9 m、10 m、12 m、14 m，共6种工况。以土体最大水平位移及基坑整体稳定性系数为评判标准，来判断最佳的桩长。

图2为桩长与基坑土体最大水平位移的对应关系，对应上述6种工况的最大水平位移分别为：24.67 mm，14.88 mm，12.24 mm，10.78 mm，10.65 mm，10.58 mm。从中可以看出当桩长由7 m增加至9 m时，最大水平位移急剧减小。而到桩长增加至10 m附近时，土体最大水平位移区域稳定，说明此时增加桩长对支护效果已经影响不大。因此可以通过土体最大水平位移与桩长的关系来确定合理桩长，为了增加说服力，本文还计算了各种工况下的基坑整体稳定性系数，计算结果见图3。

图2 桩长与最大水平位移的关系Fig.2 Correlation between the pile length and the maximum horizontal displacement

图3为桩长与基坑整体稳定性系数的关系，从图中可以看出随着桩长的增加稳定性系数也在增加。5种工况对应的稳定性系数分别为1.073，1.154，1.227，1.268，1.295，1.318，从稳定性系数来看，当桩长为10 m时已达1.268，说明桩长继续增加已无必要。

图3 桩长与稳定性系数的关系Fig.3 Correlation between the pile length and FOS

通过上述分析，将桩长与基坑土体最大水平及基坑整体稳定性进行了对比，认为最合理桩长应在10 m左右。本文将继续分析土体性质的变化对合理桩长的影响。

3.2 摩擦角对桩长的影响

首先变化土体的摩擦角，以此来分析摩擦角对合理桩长的影响，将摩擦角分别设置为11°，14°，17°，20°，23°，26°，其他因素保持不变，共6种工况。在确定每种工况的合理桩长时，均采用上述分析的方法，即通过位移及稳定性系数与桩长的对比分析来确定。

图4为各工况下的土体最大水平位移与桩长的关系曲线。从曲线形态来看，各种工况下最大水平位移随桩长的变化特征相似。从图中也可以看出，随着摩擦角的增大，土体最大水平位移逐渐减小，而且变化曲线的缓和段逐渐前移，即最佳桩长逐渐减小，说明摩擦角的增大促使了最佳桩长的减小。经过与稳定性系数计算结果的对比得到了相同的结论，由于篇幅所限，不再给出稳定性计算的所有结果。摩擦角11°～26°对应的最佳桩长条件下基坑整体稳定性系数分别为1.279，1.275，1.265，1.268，1.274，1.280，嵌固稳定性系数计算结果分别为1.173，1.171，1.168，1.165，1.171，1.178，均满足规范要求，且与基坑整体稳定性系数计算结果一致。

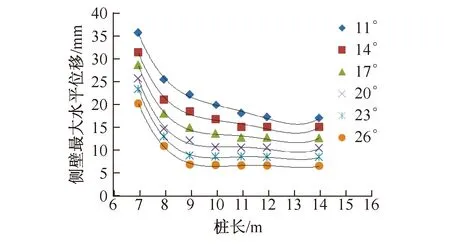
图4 桩长与最大水平位移的关系Fig.4 Correlation between the pile length and the maximum horizontal displacement

为了便于对比分析，将摩擦角与最佳桩长建立关系，如图5所示。摩擦角从11°增加至26°时，最佳桩长从12 m减小至9.5 m。图中还对两者的关系进行了拟合，相关关系公式为

y=-0.181x+13.848，

(1)

式中，y为最佳桩长，x为土体摩擦角。

拟合的相关系数达0.937 7，拟合精度较高，说明摩擦角与最佳桩长有着明显的线性对应关系。

3.3 黏聚力对桩长的影响

在分析土体黏聚力的变化对最佳桩长的影响时，将黏聚力变化为21 kPa，24 kPa，27 kPa，30 kPa，33 kPa，36 kPa。其他因素保持不变，摩擦角仍为20°，其他参数见表1。计算结果见图6、图7。

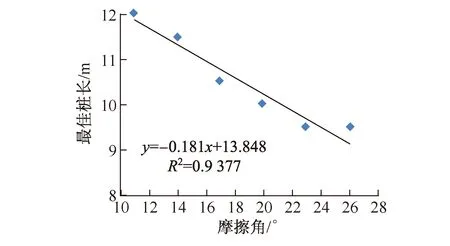
图5 最佳桩长与摩擦角的关系Fig.5 Correlation between the best pile length with the friction angle

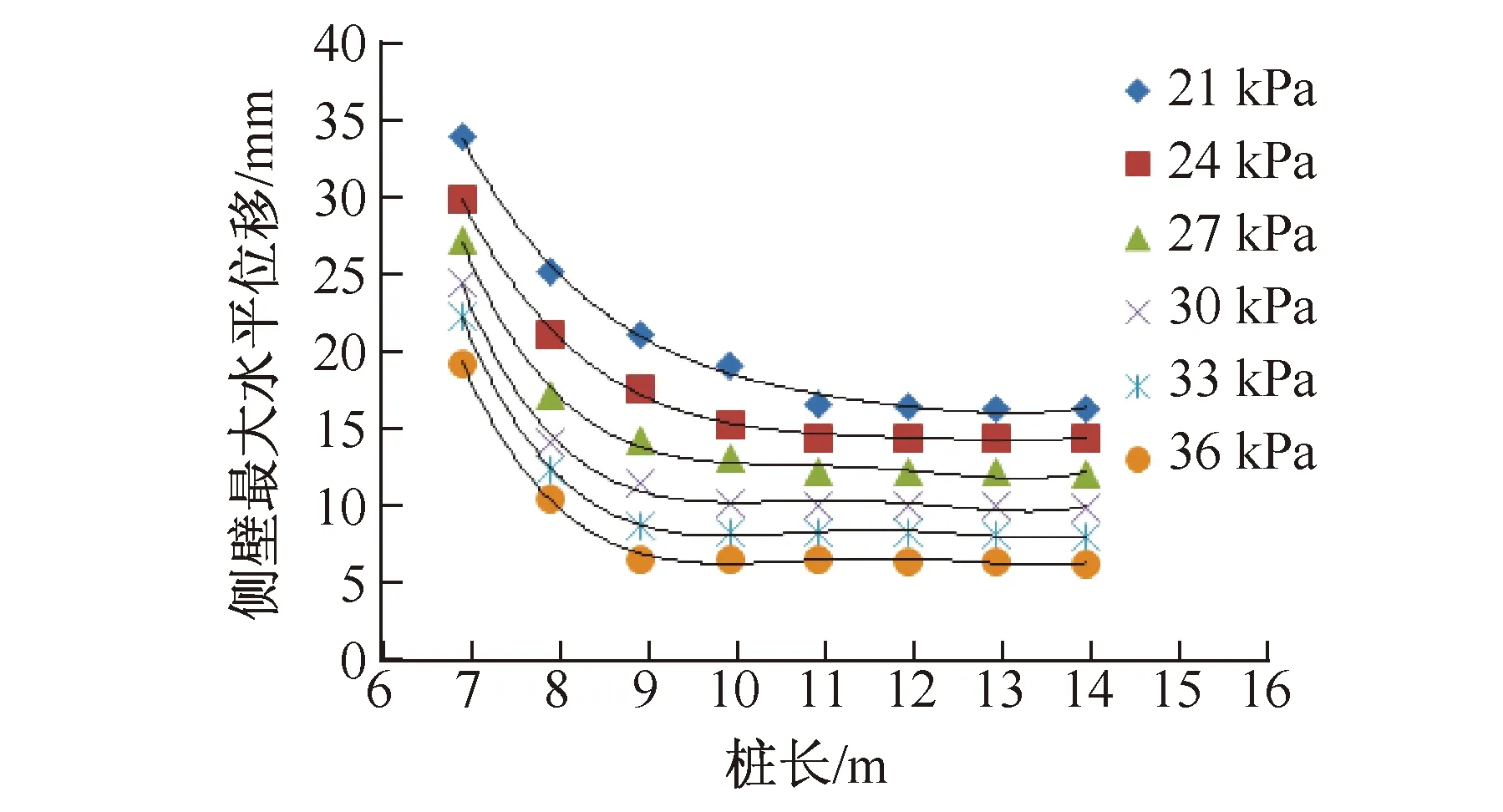
图6 桩长与最大水平位移的关系Fig.6 Correlation between the pile length and the maximum horizontal displacement

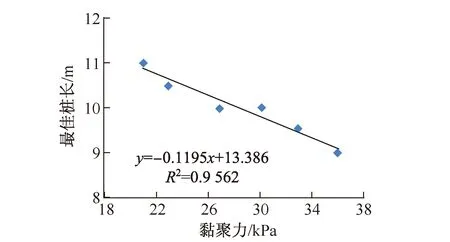
图7 最佳桩长与黏聚力的关系Fig.7 Correlation between the best pile length and the friction angle

图6为各工况下桩长与土体最大水平位移的关系。曲线形态特征与摩擦角因素分析时相似，最大水平位移随桩长的增加仍然是由快速下降段至缓和段。另外，随着黏聚力的增大，缓和段位置逐渐前移，即最佳桩长逐渐减小，与摩擦角因素分析时结论一致。黏聚力21 kPa增加至36 kPa时最佳桩长对应的基坑整体稳定性系数分别为1.269，1.275，1.266，1.277，1.281，1.279，嵌固稳定性系数计算结果分别为1.164，1.172，1.165，1.175，1.181，1.179，均满足规范要求，且与基坑整体稳定性系数计算结果一致。

图7为最佳桩长与黏聚力的关系曲线，黏聚力从21 kPa增加至36 kPa时，最佳桩长从11 m减小至9 m，说明随着土体黏聚力的逐渐增加，最佳桩长逐渐减少。图中对两者的关系拟合结果为

y=-0.119 5x+13.386

(2)

式中，y为最佳桩长，x为土体黏聚力。

拟合的相关系数达0.956 2，拟合精度较高，两者仍然成线性关系。

比较土体黏聚力、摩擦角与最佳桩长的相关关系公式时发现，摩擦角与最佳桩长的关系公式斜率为-0.181，而黏聚力与最佳桩长的关系公式斜率-0.119 5，其中摩擦角的斜率绝对值要比黏聚力的大，说明对应最佳桩长来说，摩擦角因素更为敏感。

3.4 开挖深度对桩长的影响

通过前述分析可知土体抗剪强度参数对桩长的设置有一定的影响，另外基坑开挖深度的大小对最佳桩长的设置势必产生影响，因此本文对开挖深度这一因素也进行了分析。在分析基坑开挖深度对最佳桩长的影响时，将开挖深度设置为2 m，4 m，6 m，8 m，10 m，共5种工况，仍然以土体最大水平位移及基坑整体稳定性系数为评判标准。为了更合理地分析问题，运用插入比的概念来分析桩长因素的影响，计算结果见图8、图9。

图8为5种工况下土体最大水平位移与插入比的关系。从曲线形态特征来看，与前述分析摩擦角、黏聚力因素时形似，只要在基坑开挖深度为2 m时，曲线的快速变形段与缓和段区别不明显，这也说明基坑开挖深度较浅时，设置灌注桩这种支护形式显得没有必要。

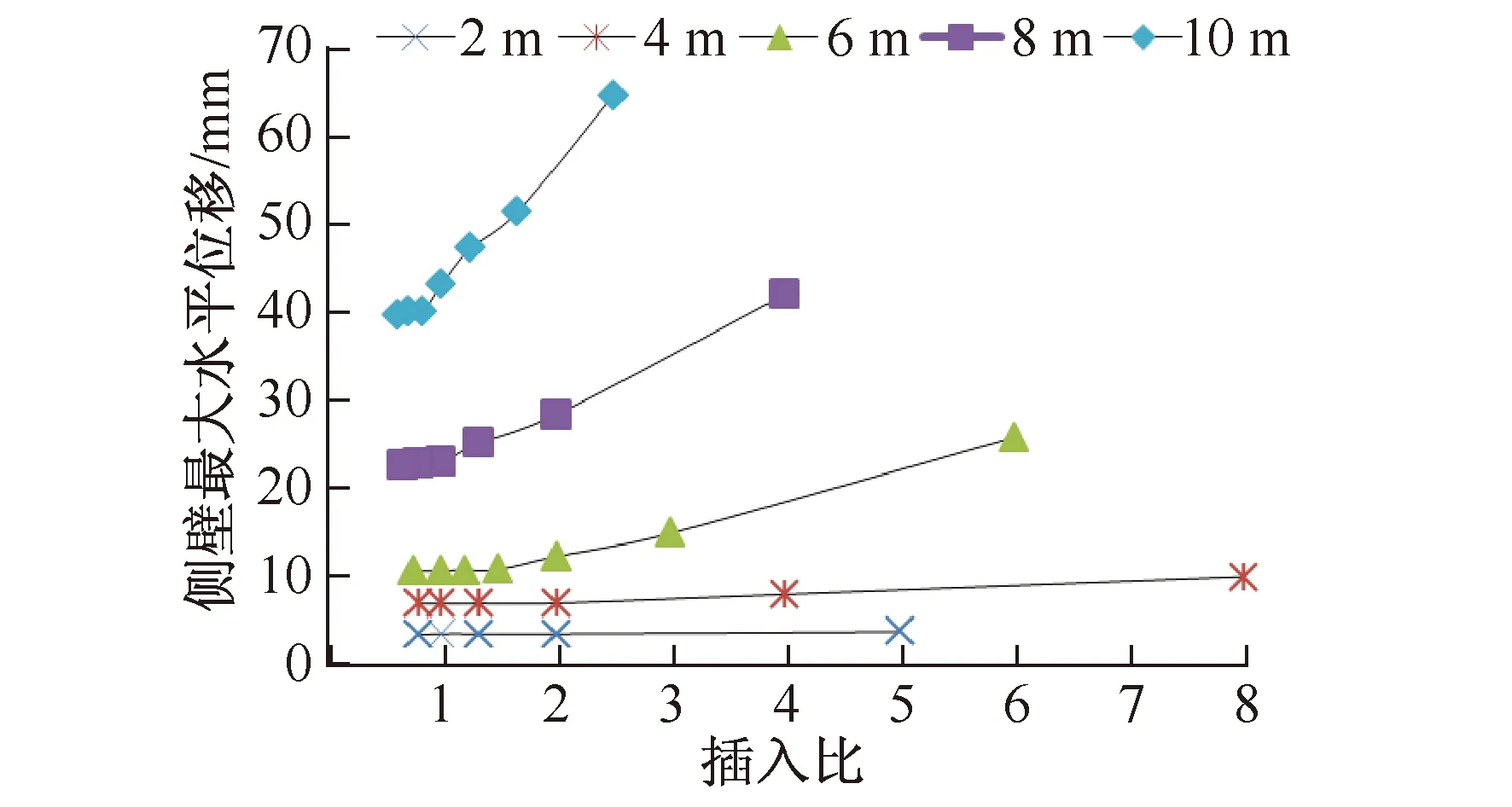
图8 插入比与最大水平位移的关系Fig.8 Relationship of insert ratio with maximum horizontal displacement

从图8中还以看出，当基坑开挖深度为8 m时，最后的缓和段中土体最大水平位移仍在20 mm以上，说明土体变形较大。当基坑开挖深度为10 m时，缓和段的土体最大水平位移在40 mm左右，变形已经超出了一般允许值[10]，这也说明当基坑开挖深度较大时，采用本文中所述的单排灌注桩支护形式已经不能满足工程需求。

图9为各工况下最佳插入比所对应的基坑整体稳定性系数。开挖深度2～10 m对应的插入比分别为3.33，2.00，1.50，0.94，0.80，从该图中也可以看出，基坑开挖深度达8～10 m时稳定性系数显著降低。基坑开挖空2～10 m的嵌固稳定性系数计算结果分别为1.274，1.231，1.188，1.135，1.128，与基坑整体稳定性系数计算结果一致。

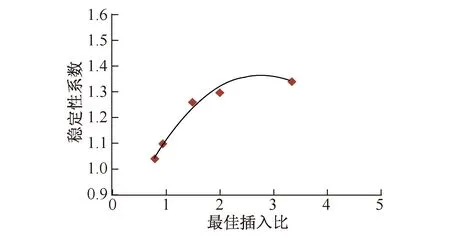
图9 最佳插入比与稳定性系数的关系Fig.9 Relationship of best insert ratio with stability factor

图10为最佳插入比与基坑开挖深度的对应关系。从图中可以看出，与摩擦角、黏聚力因素相比，开挖深度与最佳桩长不再是线性关系，而是成幂函数关系。其相关关系公式为

y=6.144 7x-0.866

(3)

式中，y为最佳插入比；x为基坑开挖深度。

拟合的相关系数达0.994 6，拟合精度要高于前述两种因素。从图10中也可以看出，随着基坑开挖深度的增加，最佳插入比呈减小趋势。

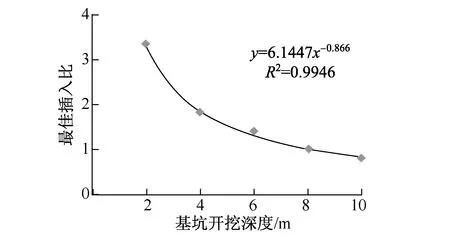
图10 最佳插入比与开挖深度的关系Fig.10 Relationship of best insert ratio with excavation depth

为了便于比较三种因素的影响程度，用线性拟合最佳插入比与基坑开挖深度的关系式为

y=-0.293x+3.431

(4)

其直线斜率为-0.293，与摩擦角的-0.181、黏聚力的-0.120相比，绝对值最大，也说明基坑开挖深度对最佳桩长的设置影响最大。

4 结 论

通过分析土体摩擦角、黏聚力以及基坑开挖深度对基坑支护桩桩长设置的影响，本文得到了以下几点认识：

(1) 在分析最佳桩长时发现，土体最大水平位移与桩长的关系为：最大水平位移随着桩长的增加先是快速减小，然后趋于稳定，即存在快速段和缓和段。

(2)通过三个因素的分析，认为其中基坑开挖深度对桩长的设置影响最大，而土体黏聚力影响最小，土体摩擦角居中。

(3)土体摩擦角、黏聚力成线性关系，其值越大，最大桩长越小。基坑开挖深度与最佳插入比成幂函数关系，且与最佳插入比的相关系数要高于摩擦角与黏聚力。

[ 1 ] 孔德森，张秋华，史明臣.基坑悬臂式倾斜支护桩受力特性数值分析[J].地下空间与工程学报，2012，8(4)：742-747.

Kong Desen, Zhang Qiuhua, Shi Mingchen. Study on the bearing behavior characteristics of cantilever inclined retaining pile for foundation pit[J]. Chinese Journal of Underground Space and Engineering, 2012,8(4):742-747.(in Chinese)

[ 2 ] 高广运，杨成斌，高盟，等.持力层对大直径扩底灌注桩竖向承载性状的影响[J].岩土工程学报，2012，34(7)：1184-1191.

Gao Guangyun, Yang Chengbin, Gao Meng, et al. Influences of bearing stratum on vertical bearing behaviors of large diameter cast-in-place belled piles [J].Chinese Journal of Geotechnical Engineering, 2012,34(7): 1184-1191.(in Chinese)

[ 3 ] 孙元奎，陈永，陈华顺.淤土地基灌注桩水平承载特性试验及数值计算[J].公路，2012，1：78-82.

Sun Yuankui, Chen Yong, Chen Huashun. Experiment and numerical analysis of lateral load-carrying behavior of grouting piles in silty foundation[J]. Highway, 2012,1: 78-82.(in Chinese)

[ 4 ] 王忠福，刘汉东，贾金禄，等.大直径深长钻孔灌注桩竖向承载力特性试验研究[J].岩土力学，2012，33(9)：2663-2670.

Wang Zhongfu, Liu Handong, Jia Jinlu, et al. Experimental study of vertical bearing capacity behavior of large-diameter bored cast-in-situ long pile [J]. Rock and Soil Mechanics, 2012,33(9): 2663-2670.(in Chinese)

[ 5 ] 吴刚，白冰，聂庆科.深基坑双排桩支护结构设计计算方法研究[J].岩土力学，2008，29(10)：2753-2758.

Wu Gang, Bai Bing, Nie Qingke. Research on calculation method of double-row piles retaining structure for deep excavation [J]. Rock and Soil Mechanics, 2008,29(10): 2753-2758.(in Chinese)

[ 6 ] 赵志缙,赵帆.深基坑工程技术的进步与展望[J].建筑技术，2003，34(2)：88-94.

Zhao Zhijin, Zhao Fan. Progress and prospects of deep foundation pit technology[J]. Architecture Technology, 2003,34(2):88-94.(in Chinese)

[ 7 ] 汪龙兵.邻近既有线深基坑支护方案优化与施工安全研究[J].铁道建筑，2013，4：101-104.

Wang Longbing. Adjacent to the existing line of deep foundation pit optimization and construction safety research[J]. Railway Engineering, 2013,4:101-104.(in Chinese)

[ 8 ] Itasca Consulting Group Inc. FLAC users manual(version5.0)[M].Minneapolis:Itasca Consulting Group Inc,2005:1-3.

[ 9 ] 刘波，韩彦辉.FLAC 原理、实例与应用指南[M].北京：人民交通出版社，2005.

Liu Bo,Han Yanhui. FLAC principle, application and implementation[M]. Beijing: China Communications Press, 2005.(in Chinese)

[10] 中华人民共和国住房和城市建设部.GB 50497—2009 建筑基坑工程监测技术规范[S].北京：中国计划出版社，2009.

Ministry of Housing and Urban-Rural Construction of the People’s Republic of China. GB 50497—2009 Technical code for monitoring of building foundation pit engineering[S]. Beijing: China Planning Press, 2009.