加权Orlicz-bergman类上Carleson测度

孙志玲，孙 燕

(内蒙古民族大学 数学学院,内蒙古 通辽 028000)

加权Orlicz-bergman类上Carleson测度

孙志玲，孙 燕

(内蒙古民族大学 数学学院,内蒙古 通辽 028000)

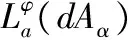
加权Orlicz-bergman类;Carleson测度;vanishing Carleson测度

0 引言

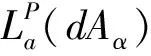
令C代表复平面，集合D={z∈C:|z|<1}称为开单位圆盘.

定义1[1]一个实值函数φ:[0,+)→[0,+)称为φ-函数，如果它是非减的连续函数且在0点等于0，当u→时φ(u)→.

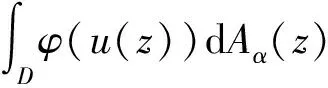
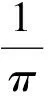
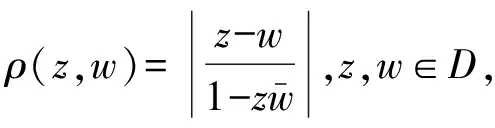
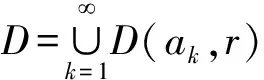
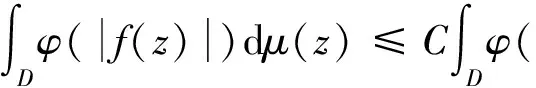
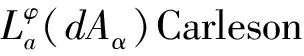
是有界的.

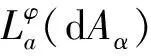
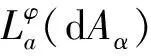
1 主要结果

引理1 设φ是凸φ-函数，α为实数，并且r>0，p>0,则存在一个正的常数C，使得对所有f∈H(D)和所有z∈D，有:

证明因为D(0,r)是中心在原点半径为s=tanh(r)∈(0,1)的欧几里得圆盘，由文献[4]命题4.13的证明过程有下面不等式成立：

根据φ为非降函数以及凸函数Jensen不等式[5]的性质，对f∈H(D)及p>0有：

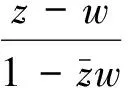
由文献[4]命题4.5，对所有w∈D(z,r)，存在正常数C1使得：

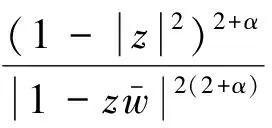
因此：

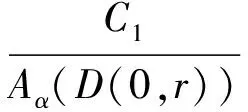
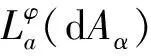
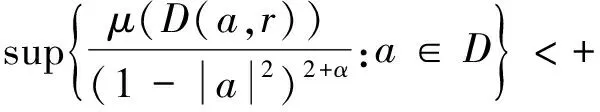
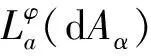
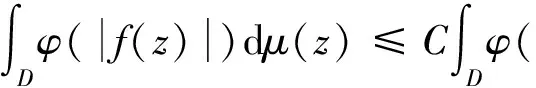
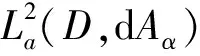
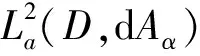
由D(a,r)的定义，知D(a,r)⊆D因此：

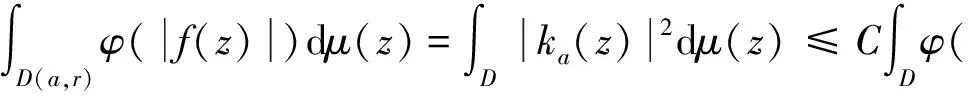
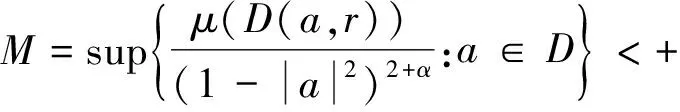
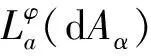
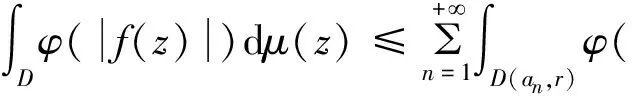
在引理1中令p=1，则存在一个正的常数C，使得对所有n=1,2,3，…，有：

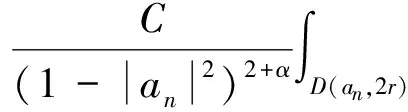
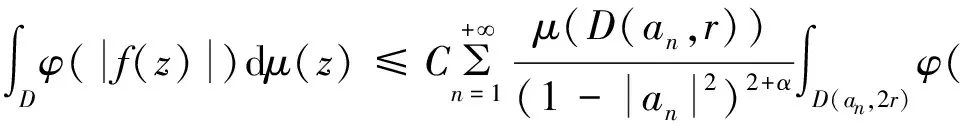
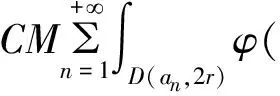
由文献[4]中的引理4.7D中每个点至多属于集合D(an,2r)中的有限个，这里用N表示，则有：

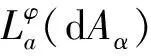
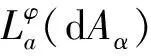
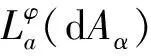
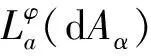
由文献[4]命题4.5，可得：

任给ε>0，存在正整数N0，使得：

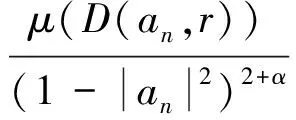
在引理1中令p=1，用与定理1同样的估计方法，则存在一个正的常数C，对所有k≥1使得：

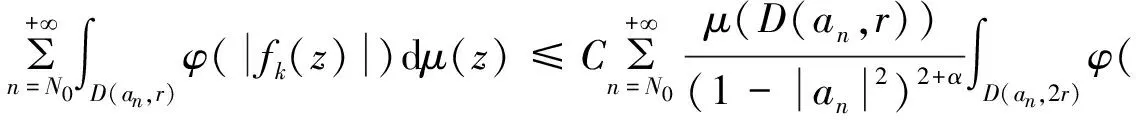
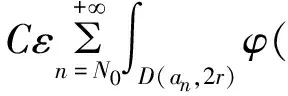
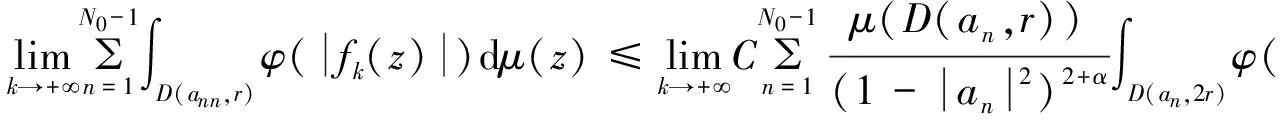
由上面两部分的估计可得：

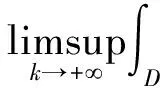
由ε的任意性，则有：

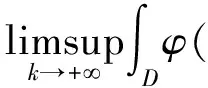
映射iP是紧的，定理证毕.

[1]路群，曹广福.Orlicz空间上的乘法算子[J].数学物理学报，2005，26A(1)：124-128.

[2]路群，曹广福.加权Orlicz-bergman空间及其上的复合算子[J].应用泛函分析学报，2005，7(4)：366-369.

[3]许安见，王晓峰.Orlicz-bergman空间及其复合算子[J].四川大学学报，2003，40(1)：24-28.

[4]Zhu Ke-he,Operator Theory in Function Spaces[M].American Mathematical Society,2007:163-173.

[5]吴从炘，王廷辅.奥尔里奇空间及其应用[M].哈尔滨：黑龙江科学技术出版社，1983:44-87.

责任编辑：高山

CarlesonMeasureonWeightedOrlicz-bergmanClass

SUN Zhiling，SUN Yan

(College of Mathematics,Inner Mongolia University for Nationalities,Tongliao 028000,China)

weighted Orlicz-bergman class;Carleson measure;vanishing Carleson measure

2014-05-04.

内蒙古民族大学博士科研启动基金项目(BS311).

孙志玲(1979- )，女，博士，讲师， 主要从事函数逼近和算子理论等的研究.

O177

A

1008-8423(2014)02-0140-04