两种流形改正近似方案的时间效率比较

马大柱，龙志超，胡凤莲

(湖北民族学院 理学院，湖北 恩施 445000)

两种流形改正近似方案的时间效率比较

马大柱，龙志超，胡凤莲

(湖北民族学院 理学院，湖北 恩施 445000)

以平面圆形限制性三体问题为基本研究模型，对比研究速度近似改正方法和速度坐标近似改正方法关于最大李雅普诺夫指数和快速李雅普诺夫指数的计算时间问题. 结果表明: 加入改正项后，速度近似改正方法的时间效率要明显优于速度坐标均近似改正方法.该研究对太阳系多体问题具有重要的应用价值.

流形改正；李雅普诺夫指数；三体问题

流形改正方案在传统低阶数值算法的基础上加入与积分常数相关的控制项抑制可以舍入误差的逐渐积累，为复杂动力系统的研究提供较高精度的数值解，可以避免因数值误差而产生的假混沌现象，是目前天体力学[1]和宇宙学[2-3]中常用的数值研究工具.文献中有两种常用的近似流形改正方案，一种是速度近似改正方法[4]，另外一种是速度坐标均近似改正方法[5].混沌指标的正确使用是非线性研究工作的重要基础，实践表明，最大李亚普诺夫指标[6]计算量少，可以直观反应相空间轨道动力学性质，在混沌动力学中经常使用.快速李亚普诺夫指标[7]相对最大李亚普诺夫指标而言具有无需重整化的优势，在相对论混沌动力学中应用更广.本文首先介绍两种数值工具，然后以平面圆形限制性三体问题为例，讨论两种近似改正方案关于混沌指标的时间效率问题.

1 数值基础

1.1 速度坐标改正方案

该方案是Nacozy[4]提出的一种流形改正方法，是最小二乘法原理[2-3]的直接应用.对于含微分动力系统，其态矢量为态矢量x，系统的p个积分满足ej(x)=0，j=1,2,…,p，p个积分对坐标和速度的偏导数可组成一含有6n列p行的矩阵E′.Nacozy改正矢量Δη与态矢量x之间满足关系：x=η+Δη，其中Δη应使得ΔηTWΔη最小化，即满足：

Δη=-W-1E′T(E→′W-1E′T)-1ε

(1)

这里W是权重矩阵，T代表转置，矩阵(E′W-1E′T)是一p×p型对称矩阵.在数值积分的每一步，数值解后都加入上述稳定项并校正，用校正后的数值解作为下一步的初始条件.

1.2 速度改正方案

Wu等[5]在上述思想的基础上，提出只对速度项的三个分量改正，即：

(2)

由于上述两种积分方案都不满足严格的不变积分关系，所以都是近似方法.

2 研究模型

本文研究模型为平面圆形限制性三体问题[8]，是天体力学中的基本模型之一，假设三体中的某一体的质量相对其它两体无限小.第三体在两主天体引力作用下作平面圆形限制性运动，在旋转坐标系中，第三体的运动微分方程表达式为：

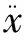
(3)

(4)

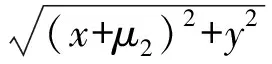
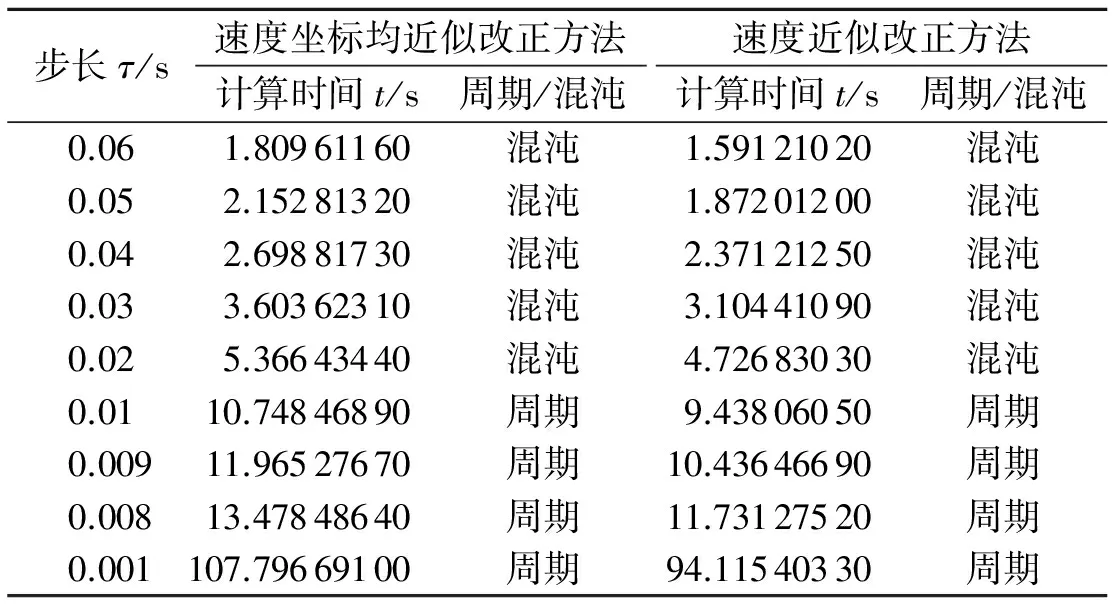
表1 两种近似改进方法关于最大李亚普诺夫指标的时间效率比较

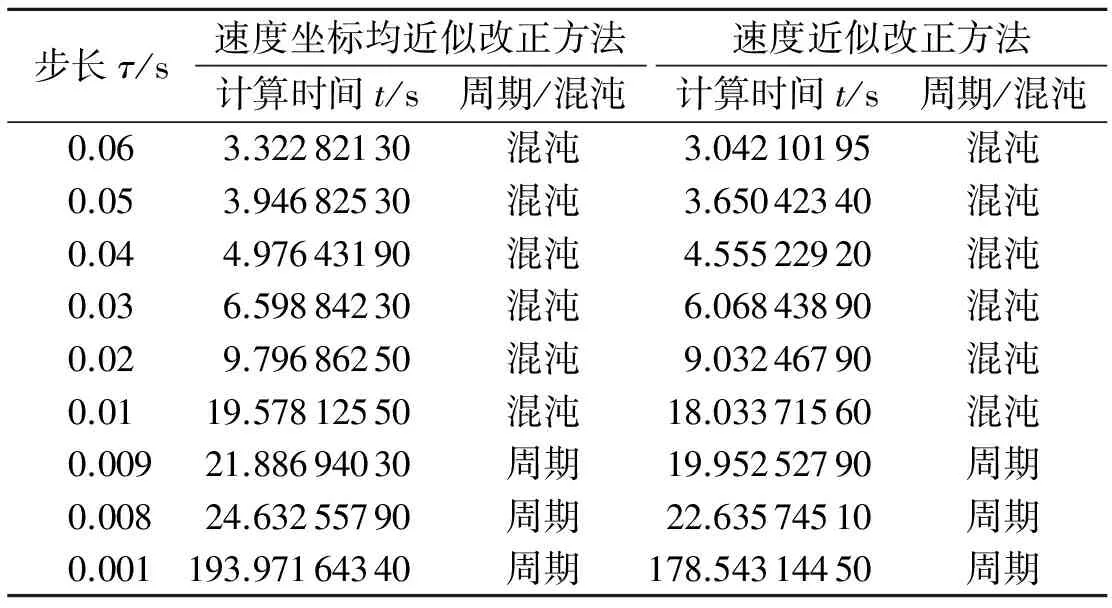
表2 两种近似改进方法关于快速李亚普诺夫指标的时间效率比较

3 混沌指标

3.1 最大李亚普诺夫指标

N维动力系统具N个李亚普诺夫指数，最大李亚普诺夫指标[6]不用计算正交化的过程且更容易反映系统的相空间动力性质.其计算表示为：

(6)

其中ξ(0)和ξ(t)代表初始时刻和t时刻相空间切矢量.

3.2 快速李亚普诺夫指标

快速李亚普诺夫指标[7]是计算两临近轨道平均指数分离比的指标，有变分法和两粒子法两种方式计算该指标.变分法中需对运动方程和变分方程同时积分，计算量较大.两粒子法只须在第一条轨道的初值上加上一个很小的常数，重新积分运动方程即可.实际计算过程中其表达式为：

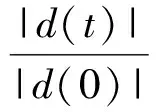
(7)

其中：d(0)是初始轨道分离值；d(t)代表任意是时刻的轨道分离值；κ为序列号.

4 结果分析

数值计算过程中首先用四阶龙格库塔方法(RK4)给出运动微分方程的基本解，然后将两种改正方案(1)和(2)分别加到基本解后作为改正项，最后以改正后的数值解计算两种混沌指标(6)和(7).最大李亚普诺夫指标的时间效率对比见表1，快速李亚普诺夫指标的时间效率对比见表2.从表中容易看出：速度近似改正方法的计算时间要少于速度坐标均近似改正方法，而且随着步长的减小，时间区别越明显，更重要的是两种方法均不会改变轨道的周期与混沌特征.一方面说明两种近似改进方法确实能准确的表现轨道运动的特点，另一方面说明只对速度部分改正并不影响系统总体运动行为，而且节省了计算时间.虽然对圆形限制性三体问题只有几秒的差别，但是对于复杂的多体系统积分，如太阳系多体问题，两者的积分效率会体现的更为明显.

[1]Ma D Z,Wu X,Zhu J F.Velocity scaling method to correct individual Kepler energies[J].New Astronomy,2008,13:216-223.

[2]Ma D Z,Wu X,Zhong S Y.Effects of the cosmological constant on chaos in an FRW scalar field universe[J].Research in Astronomy and Astrophysics,2009,9:1185-1191.

[3]Ma D Z,Wu J P,Zhang J F.Chaos from the ring string in a Gauss-Bonnet black hole in AdS5space[J].Physical Review D,2014,89:086011.

[4]Nacozy P E.The use of integrals in numerical integrations of the N-body problem[J].Astrophysics and Space Science,1971,14:40-51.

[5]Wu X,Huang T Y,Wan X S,et al.Comparison among correction methods of individual kepler energies in n-body simulations [J].AJ,2007,133:2643-2653.

[6]Froeschle C,Lega E.On the Structure of Symplectic Mappings. The fast Lyapunov indicator: a very sensitive tool[J].Celestial Mechanics and Dynamical Astronomy,2000,78:167-195.

[7]Wu X,Huang T Y.Computation of Lyapunov exponents in general relativity[J].Physics Letters A,2003,313:77-81.

[8]Simo C,Stuchi T J.Central stable/unstable manifolds and the destruction of KAM tori in the planar hill problem[J].Physica D,2000,140:1-32.

责任编辑：时凌

ComparisonofTimeEfficiencyProblemofTwoKindsofApproximateManifoldCorrectionSchemes

MA Dazhu,LONG Zhichao,HU Fenglian

(School of Science,Hubei University for Nationalities,Enshi 445000,China)

The paper discusses the time efficiency problem on the Maximum Lyapunov indicator and the fast Lyapunov indicator for two kinds of approximate manifold schemes,namely,velocity method and velocity and position method. The Planar circular restricting three-body problem is adopted as the basic model.The results show that the velocity approximate method has more priority than the velocity and position method. The research has great application value in multi-body problems in Solar system.

Manifold correction；Lyapunov indicator；three-body problem

2014-05-23.

国家自然科学基金项目(11263003).

马大柱(1983- )，男，硕士，讲师，主要从事数值计算方法和非线性动力学研究.

O317+.2

A

1008-8423(2014)02-0153-03