非奇异H-矩阵的一类判定条件
2014-08-25张俊丽韩贵春
张俊丽,韩贵春
(内蒙古民族大学 数学学院,内蒙古 通辽 028043)
非奇异H-矩阵的一类判定条件
张俊丽,韩贵春
(内蒙古民族大学 数学学院,内蒙古 通辽 028043)
非奇异H-矩阵是一类在工程技术和科学研究领域应用广泛的特殊矩阵.根据α对角占优矩阵与H-矩阵的关系,给出了非奇异H-矩阵的一类判定准则,推广和改进了已有的相关结果,数值算例说明了该判定准则的有效性.
非奇异H-矩阵;α-对角占优矩阵;不可约;非零元素链
0 引言
非奇异H-矩阵是一类重要的特殊矩阵,在控制论、电力系统理论、经济数学以及弹性力学等众多领域中都有着广泛的应用.然而其数值判定是困难的,国内外许多学者给出了非奇异H-矩阵的判定方法[1-6].本文在文献[1]的基础上,利用α-对角占优矩阵与非奇异H-矩阵的关系,给出了非奇异H-矩阵的一种判定法,对文献[2]中的结果进行了推广.
首先引入符号和定义:
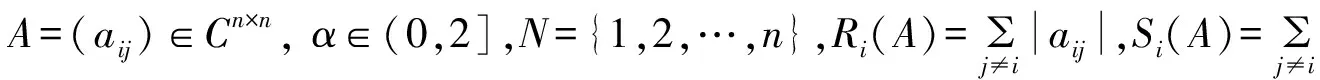
记:
N1={i∈N|0<|aii|=αRi(A)+(1-α)Si(A)}
N2={i∈N|0<|aii|<αRi(A)+(1-α)Si(A)}
N3={i∈N||aii|>αRi(A)+(1-α)Si(A)}
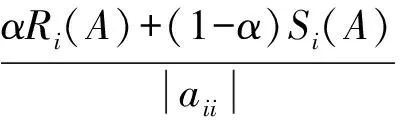
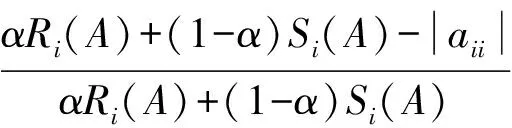
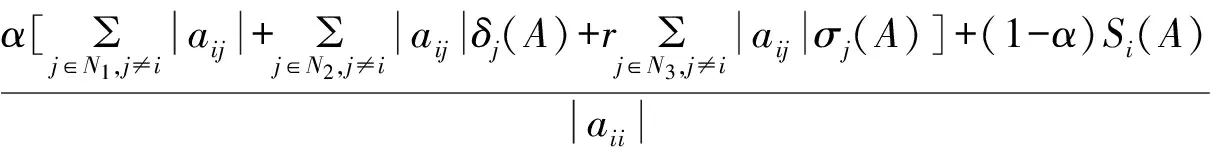

定义2A=(aij)∈Cn×n,如果∃α∈(0,1],使得∀i∈N,有:
|aii|≥αRi(A)+(1-α)Si(A)

定义3 设A=(aij)∈Cn×n,不可约,若A∈D0(α),且至少有一个不等式严格成立,则称A为不可约α-对角占优矩阵; 若A∈D0(α),并对于满足等式成立的下标i都存在非零元素链aii1,ai1i2, …,aikj,使得 |ajj|≥αRj(A)+(1-α)Sj(A),则称A具为非零元素链α-对角占优矩阵.
引理1[3]设A=(aij)∈Cn×n,α∈(0,1].若满足下列条件之一, 则A为非奇异H-矩阵:
1)A为严格α-对角占优矩阵;
2)A为不可约α-对角占优矩阵,且至少有一个严格对角占优行;
3)A具为非零元素链α-对角占优矩阵.

1 主要结果
定理1 设A=(aij)∈Cn×n,α∈(0,1],若∀i∈N2,有:
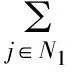
(1)
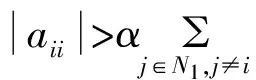
证明由r的定义知,0≤r<1;∀i∈N3,有:
r[αRi(A)+(1-α)Si(A)]≥
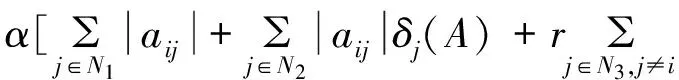
所以:
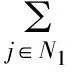
r[αRi(A)+(1-α)Si(A)]
于是:
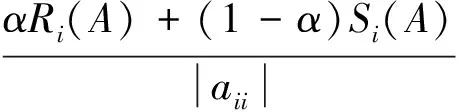
即
0≤ρi(A)≤rσi(A) (2) 由式(1),必∃ε>0,使得0<ρi(A)+ε<1,∀i∈N2,∀i∈N3, 且有下式成立: (3) 构造正对角矩阵X=diag(x1,x2,…,xn), 且令B=AX=(bij)n×n,其中: αRi(A)+(1-α)Si(A)=|aii|=|bii| 2)当i∈N2时: (1-α)Si(A)δi(A)<|aii|δi(A)=|bii| 3)当i∈N3时, ∀j∈N2, 0<δj(A)<1,由式(2)及ε>0得: ρi(A)|aii|+ε|aii|=|aii|(ρi(A)+ε)=|bii| 注:文献[1]的定理1是上述定理在α=1时的特殊情况,且该判定方法可以推广到不可约和具有非零链的情形. 定理2 设A=(aij)∈Cn×n不可约,α∈(0,1],若∀i∈N2,有: (4) 证明由于A不可约,则∀i∈N′⊂N, ∀j∈N-N′,有|aij|不全为零. 构造正对角矩阵 1)当i∈N1时: 2)当i∈N2时,由(4)式得: 又(4)式中至少有一严格不等式成立,即存在k,使得: 3)当i∈N3时,∀j∈N2,0<δj(A)<1 由引理2,类似于定理1和定理2亦可得到下面的定理. 定理3 设A=(aij)∈Cn×n,α∈(0,1],若∀i∈N2,有: (5) 且其中至少有一严格不等式成立,又对式(5)中的每一个等式成立的i,存在非零元链aii1ai1i2ai2i3…aikj,满足: 考虑矩阵: 利用本文定理1,取α=0.8,则N1={1},N2={2},N3={3,4,5},r=0.680 2,于是,|a22|δ2(A)=2.22>α[|a21|+|a23|ρ3(A)+|a24|ρ4(A)+|a25|ρ5(A)]+(1-α)S2(A)=2.17. 所以A为非奇异H-矩阵,但用文献[2]中定理1无法判断. [1]王峰.非奇异H-矩阵的判定及其在神经网络系统中的应用[J].江南大学学报:自然科学版,2012,11(1):94-98. [2]黄廷祝.非奇异H-矩阵的简捷判据[J].计算数学,1993,15(3):18-328. [3]Sun Yuxiang. An Improvement on a Theorem by Ostrowski and Its Applications[J].Northeastern Math J,1991,7(4):97-520. [4]李继承,张文修.H矩阵的判定[J].高等学校计算数学学报,1999,21(3):264-268. [5]Berman A,Plemmons R J.Nonnegative Matrix in the Mathematical Sciences[M].New York:Academic Press,1979. [6]杨亚强.非奇异H-矩阵的一个实用充分条件[J].宝鸡文理学院学报,2012,32(1):32-35. 责任编辑:时凌 SomeSimpleConditionsforNonsingularH-matrices ZHANG Junli,HAN Guichun (School of Mathematics,Inner Mongolia University for the Nationalities,Tongliao 028043,China) NonsingularH-matrix is a kind of special matrix with applications in the field of engineering and scientific research. In this paper, some new criteria are given according to the relations ofα-diagonally dominant matrices and nonsingularH-matrices,which extend and improve some related results. Effectiveness of these criteria is illustrated by numerical examples. nonsingularH-matrix;α-diagonally dominant matrix; irreducible; nonzero elements chain 2014-05-02. 内蒙古民族大学自然科学基金(NMD1305). 张俊丽(1980- ),女,硕士,讲师,主要从事数值代数及应用的研究. O151.21 A 1008-8423(2014)02-0144-04
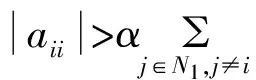
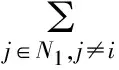
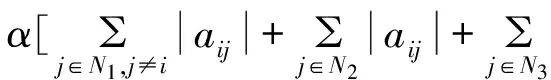
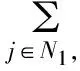
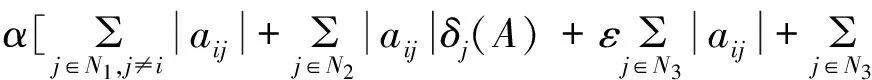
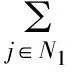
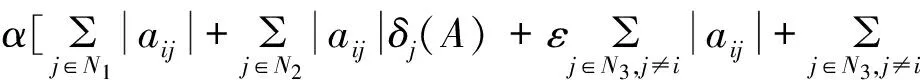
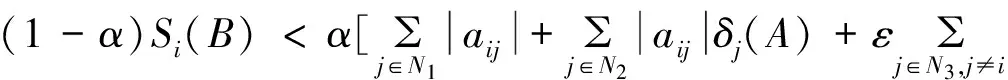
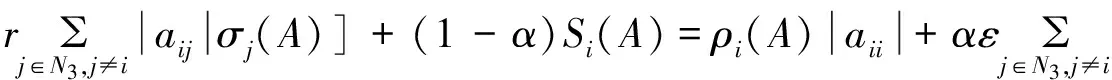
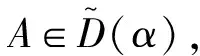
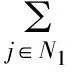
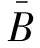
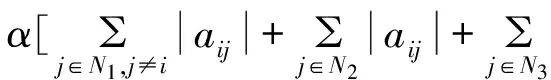
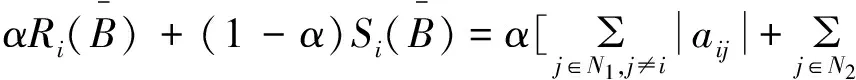
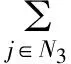
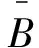
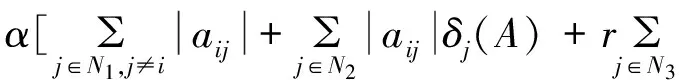
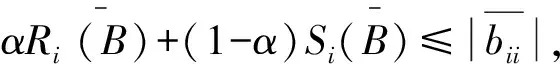
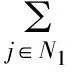
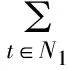

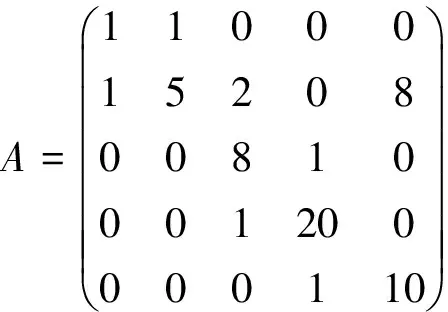
2 数值算例