培养学生自主探究的一种教学模式
2014-08-22江苏省沛县中学
肖 爽(江苏省沛县中学)
本文以高中数学苏教必修一《指数函数》(第1课时)为例,就具体教学环节的处理和案例所体现出的教学理念作一些分析.
一、教学环节
1.问题引入
某种细胞分裂时,由1个分裂成2个,2个分裂成4个,……试写出该细胞分裂的数学模型(设1个细胞分裂x次后,得到的细胞个数为y,在下表中x依次取值1、2、3……归纳出y与x的函数关系式,并观察图象).

(说明:本部分用Excel软件制作,当学生输入相应的x与y的值后,其右边的图象会随数据动态产生)
以问题形式引入,重视学生的参与,强调从“形”入手增加学生对指数函数的感性认识.课件动态处理数据的功能使学生在自主操作过程中充分与计算机进行互动.
2.描点法画图象
结合以下问题探讨:
(1)用描点法画y=2x图象时,请多尝试几组x的值,比较哪一组数据更能精确描述函数y=2x的图象(可与同学进行对比).
(2) 由y=2x的图象能画出栏中的数据在正确位置上输入论.

(说明:本部分用Excel软件制作,输入x的值后y=2x的值便自动给出,其相应图象会随数据动态产生,而值要自己输入)
案例比较注重让学生亲身体验画图象的过程,要求学生自己输入x值,2x值与图象都由计算机帮助处理,使学生有更多时间尝试输入几组x值进行图象对比,在强调了学生的个性差异的同时又能让学生在对比中学会分析问题.对于函数案例中不直接提供数据,而是提示学生利用现有数据进行观察,从而让学生在“数形”两方面深刻地理解了两个函数的关系与对比,既强调了学生的主动参与和探究,又注重培养学生收集数据、处理数据的能力.
3.研究函数性质
结合问题自主操作,探讨y=ax的性质:
(1) 当 a=1,a=0,a<0时情况如何,为什么?
(2) 对a>1时函数图象与性质进行分析,
①定义域是多少?
②图象的分布(值域) .
③图象是否过一定点,为什么?
④函数的单调性.
(3) 当0 (4) 对比 y=ax和 y=a-x的图象与性质. (5)当a>1时,要使图象在y=1上方,x的取值范围是多少? (6)探究性问题:当a变化时,函数图象的变化规律是什么? (7)比较数21.5与21.6的大小,并探讨此类题的解法. 案例把画图象和性质探讨作为本节课的重点.本案例利用《几何画板》强大的交互功能,设计循序渐进的问题链,让学生在动态的、开放的“数学实验室”里自主探究.学生实时拖动动点B,改变y=ax中a的值,观察连续变化的函数图象并进行个性化的研究(相比较,案例A只是孤立地研究了a=2和的两种静止状态).通过学习,学生对以下几点应该有了深刻认识: ①y=ax中a的取值范围; ②a>1时函数的定义域、值域、单调性等; ③学会对a>1与0 ④利用图象解不等式ax>1; ⑤利用单调性比较大小; ⑥对过定点的探究; ⑦当a>1时,a变化时函数图象的变化趋势. 其中①②③属基础知识范畴;④⑤属图象与性质的应用范畴;⑥⑦属进一步探究范畴.可以说,通过“做数学”,学生不但对指数函数从“数”和“形”两方面都有了较深刻的理解,而且会逐渐体会到变化情形中有不变性与变化性,并由操作感知进一步升华为变化统一的数学思想. 例 1:已知指数函数 f(x)=ax(aφ0,且 a≠1) 的图象经过点 (3,π),求 f(1),f(-3) 的值. 例2:利用指数函数的性质,比较下列各题中两个值的大小: (1) 1.7a与 1.7a+1(2) 0.8-0.1与 0.8-0.2 设计较简单的练习,能使学生对指数函数图象性质进行简单应用、巩固整理. 本案例属网络探究课,强调学生自主探究,在学习过程中,教师不直接将教学内容讲授给学生,而是设计一些具有诱导性的问题,使学生利用问题链,通过自主操作参与知识和规律的发现与验证,引导自己不断操作尝试,在不断错误和修正错误的过程中进行一步步深入探索. 学生的学习是主动的,具有探究性,又具有合作性.学生始终围绕问题链进行自主探究,若在数据的收集处理与对动态图象的操作中发现问题,学生或多次尝试,或请教老师,或与同学讨论以解决问题. 本案例侧重基础知识的掌握,更注重培养学生的自主探究能力.整个教学过程从提出问题开始到解决问题结束,引导学生在学习中做到“学中有探”、“探中有学”.在解决问题的过程中,通过发现新问题、解决新问题,培养学生的探究意识、创新精神和实践能力,使学生学会自主学习、探究学习和合作学习. 案例导学教学方法使学生学习的目标更加明确,重点更加突出,问题设计更加具有针对性,有效调动了广大学生学习的积极性.教师主观能动性的充分发挥和设计巧妙的学案,使“学例导学”教学法在新课程的教学中再放光彩.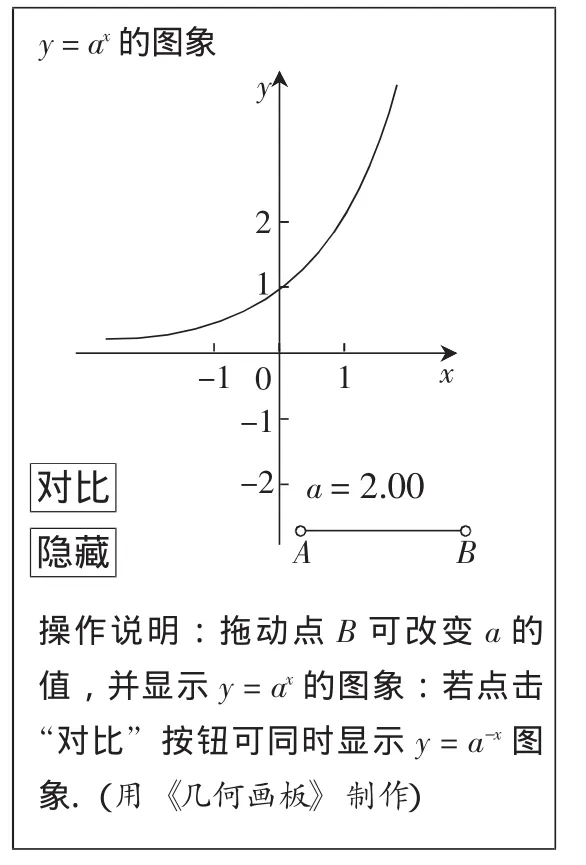
4.练习巩固


二、教学理念
1.课堂教学模式
2.学生学习方式
3.学生能力方面
