利用GPU实现平行扇束投影的数据仿真

胡修炎

(枣庄学院 数学与统计学院，山东 枣庄 277160)

0 引言

由于CT理论中的平行束投影和锥束投影的概念分别与计算机图形学中的正交投影和透视投影的概念一致.CT理论中的X光源和探测器分别对应于计算机图形学中的摄像机和渲染目标.由于GPU利用专用的纹理映射硬件计算纹理坐标(投影地址)，并能够并行处理多个被投影的数据，因此利用GPU可以将投影操作的速度提升一到两个数量级(与用CPU执行投影操作相比较).

1 预备知识

1.1 多层扇束投影模型

三代扇束扫描模式下探测器为线探测器或弧形探测器，在扫描过程中射线源和探测器固定不动，转台旋转一周(如图1所示).

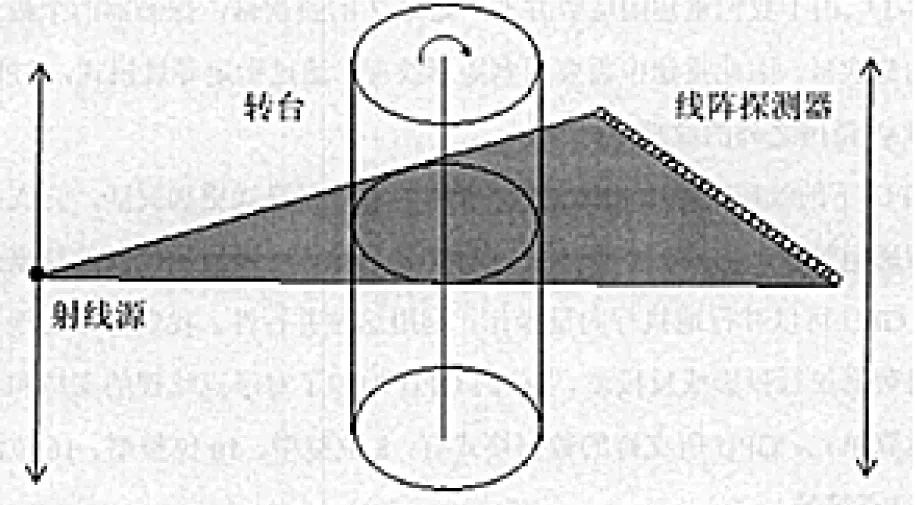
图1 扇束CT扫描示意图

1.2 GPU下CT数据的存储方式

GPU程序中的数据以纹理的格式存储，GPU下的纹理对应CPU程序中的数组，二维纹理和三维纹理分别与二维数组和三维数组相对应.在GPU程序中，CT数据需要以类似于数组的纹理形式存储.纹理的纹素相应于数组的元素.纹素的纹理坐标相应于数组元素的指标.与数组元素指标有所不同,如图2所示.

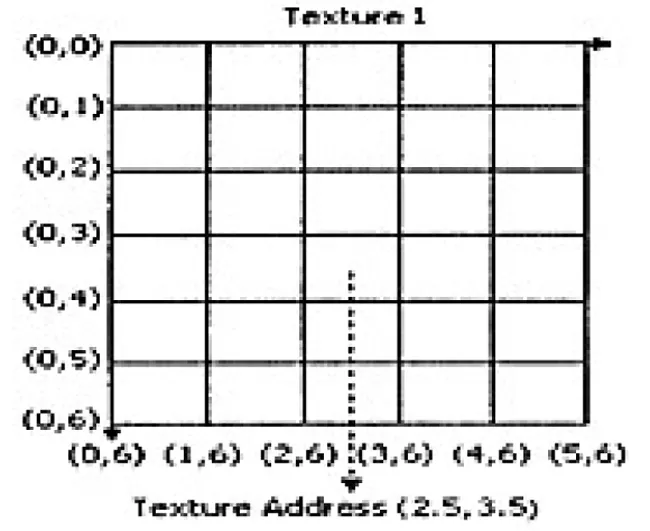
图2 矩形纹理的纹理坐标

GPU下的纹理数据格式比CPU下的数组数据格式更加灵活，它支持单通道、四通道等纹理格式.单通道纹理的纹素是标量;四通道纹理的纹素是4维向量.GPU可以并行地执行向量操作，利用这种并行性，我们可以实现并行地对四组数据进行投影或反投影.

2 平行扇束投影的GPU数据仿真

2.1 基于二维纹理的体渲染

基于二维纹理的体渲染:体数据按其空间顺序被存储于一组二维纹理中.被重建的长方体由一组等间隔的平行的长方片代表，通过纹理映射将二维纹理贴到这些长方片上，然后渲染这些长方片，打开alpha混合，最后将渲染结果累加即可得到三维体数据的投影.

这种方法的优点是插值少，它只在每个二维纹理中做插值，而二维纹理之间没有插值运算，所以缺点是绘制效果差，尤其当平行的长方片与视点方向平行时无法应用二维纹理.

2.2 数值仿真原理

仿真方法是基于二维纹理的仿真，与二维纹理的体绘制有所不同，体绘制的目的是将渲染的结果最终显示在屏幕上，而我们是要得到仿真数据，因此需要将渲染后的数据读回内存存成数据文件.并且体渲染的结果一般是8位的数据，因为人眼的分辨没有那么高，而仿真数据要求是32位的，最低也要16位的数据，因此计算量要比体绘制大的多，需要用到浮点纹理.

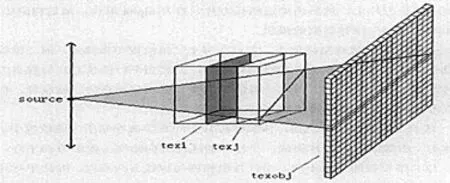
图3 仿真示意图

如图3所示模型是在定义在立方体内，用GPU通用计算方法实现数据的仿真(以下简称GPU-CT)，首先需要将数据用纹理来表示，如图所示将立方体划分为若干切片，每个切片绑定成不同的纹理.如图3所示立方体中蓝色和黄色切片分别与纹理texi,texj绑定;根据需要将立方体划分为N个切片，并分别与纹理tex0,tex1……texN-1绑定，则立方体数据就可以由这N个有序纹理来表示.

图3中的方格区域为面探测器，也可以说是投影目标区我们记做texobj.在实现仿真的过程中纹理tex0,tex1……texN-1将依次渲染到texobj，所有纹理渲染结束后texobj中的数据就是模型在某一角度下的投影，模型旋转换一个角度后，进行同样的过程就得到另一个角度的投影.

以上方式模型旋转范围在正负45度之间时得到的仿真数据是可以的，但当模型旋转的角度超出了正负45度范围时，texi与渲染目标texobj所成角度比较大，如图4所示texi与texobj成60度夹角时，texi中的16个数据投影到texobj中8个探测器上，会造成较大的误差.

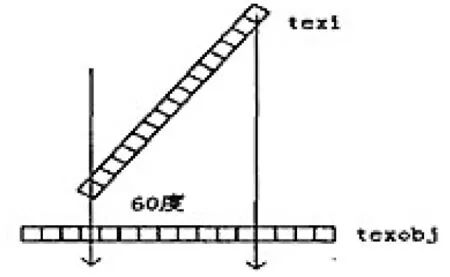
图4 texi与texobj夹角

为减小纹理texl与渲染目标texobj夹角过大引起的误差，应始终控制夹角在正负45度之间.模型旋转超过这个范围时，可以通过沿与原纹理垂直方向重新划分切片的方法来避免角度过大引起的误差.

2.3 利用GPU实现CT数据仿真具体步骤

以仿真256*256投影数据为例

步骤1:三维数据模型划分，划分为256片数据(可以根据具体的需要)，这样每一片数据大小为256*256

步骤2:每一片数据做成256*256大小的纹理，得到256片纹理，分别编号为tex0,tex1……tex255

步骤3:建立两个32位floating-pointpbuffer作为纹理渲染目标记作texobj其中texobj中初值为0.0

步骤4:将tex0渲染到目标texobj做混合运算texobj=texobj+texi;继续将tex1渲染到目标作混合运算，如此循环进行直到将tex255渲染到目标texobj，此时目标中的数据就是模型在这一角度下的平行投影数据.

2.4 仿真效果:

模型为一个大圆柱体，圆柱体内部各个方向均匀8个小圆柱体，小圆柱体深浅高度不同，以下为利用GPU实现CT数据仿真的不同角度透视图.

每片纹理大小为256*256，投影数据大小为256*256时CPU上仿真一个投影数据平均所用的时间为5.635s，GPU仿真一个投影数据平均所用的时间为0.508s，可以看出用GPU做CT数据仿真效率有了很大的提高.

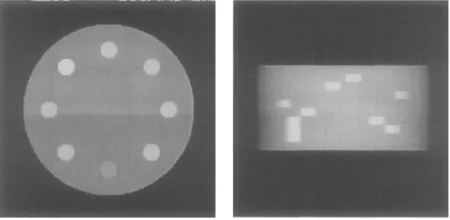
图5模型的正面透视图图6模型的侧面透视图

图7模型旋转30度透视图图8模型倾斜15度透视图

3 结论

本文利用GPU通用计算技术实现了三维CT数据仿真，与利用CPU三维CT数据仿真相比效率大大提升，仿真256*256大小的投影数据，效率大约提高10倍.数据越复杂效率对比越明显，在数据仿真方面有较高的应用价值.

针对本文的研究内容及结果，我们发现还存在一些问题有待进一步研究.利用GPU实现三维数据仿真，其中存在数据精度的问题.主要由两方面引起一方面是由GPU自身的问题引起的，另一方面对模型的分割不能划分足够细，划分的越细需要的纹理越多，而GPU的显存大小是很有限的.下一步将对如何提高仿真精度进行研究.

[1]Nathan A, Carr, Jesse D, Hall, John C Hart. The Ray Engine[A].In Proceedings of Graphics Hardware, Saarbrucken, 2002,37～46.

[2]Timothy J. Purcell, Ian Buck, William R. Mark, Pat Hanrahan. Ray Tracing on Programmable Graphics Hardware[J]. ACM Transactions on Graphics (Proceedings of SIGGRAPH), 2002,21(3):703-712.

[3]Naga Govindaraju, Stephane Redon, Ming C Lin, Dinesh Manocha. COLLIDE:Interactive Collision Detection Between Complex Models in Large Environments Using Graphics Hardware[A].In Proceedings Graphics Hardware, San Diego, 2003,25～32.

[4]Naga Govindaraju, Avneesh Sud, Sung-Eui Yoon, Dinesh Manocha. Parallel Occlusion Culling for Interactive Walkthroughs using Multiple GPUs[R]. The University of North Carolina at Chapel Hill, Carolina, UNC Computer Science Technical Report TR02-027,2002.

[5]Scott Larsen E, David McAllister. Fast Matrix Multiplies using Graphics Hardware[A].In Proceedings of Supercomputing, Denver, 2001, 55～60.

[6]Jesse D, Hall，Nathan A, Carr, John C Hart. Cache and Bandwidth Aware Matrix Multiplication on the GPU[R]. University of Illinois at Urbana-Champaign, Champaign, UIUCDCS-R-2003-2328, 2003,4.

[7]Chris J, Thompson, Sahngyun Hahn, Mark Oskin. Using Modern Graphics Architectures for In General-Purpose Computing: A Framework and Analysis[A]. In Proceedings of International Symposium on Microarchitecture, Istanbul, 2002,306～317.