新逻辑主义的困境与二阶分层概括

刘靖贤

（辽宁大学哲学与公共管理学院，辽宁沈阳110136）

一、逻辑主义从弗雷格到蒯因

弗雷格的《算术基本规律》在实质上是由二阶逻辑和公理V构成的理论[1]。二阶逻辑是在一阶逻辑的基础上得到的，它不仅包括关于二阶量化的公理，还包括标准概括公理，后者是说，任意可表达公式都可以断定一个概念的存在，

公理V是说，概念X的外延和概念Y的外延相等当且仅当X和Y等价，

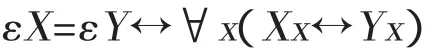
其中ε是外延算子。然而，公理V与概括公理导致罗素悖论。从证明论角度看，可以用外延算子定义属于关系，

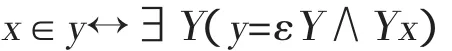
然后，根据概括公理，可以断定“不属于自身”这个概念的存在，即［x：x∉x］；再根据公理V，可以得到这个概念的外延，即 ε［x：x∉x］。由此可得，

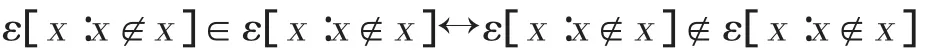
即“不属于自身”这个概念的外延属于自身当且仅当它不属于自身。从模型论角度看，概括公理要求，如果一阶变元的取值范围是D，则二阶变元的取值范围是 （D），即D的幂集；而公理V要求，存在二阶变元和一阶变元之间的一一对应。但是，根据康托对角线定理，这两个要求不能同时满足。

为了避免悖论，罗素和怀特海在《数学原理》中给出了类型论[2]。类型论在实质上是由直谓概括公理、还原公理、无穷公理和选择公理构成的。类型论被表述在高阶逻辑中，它包括：一阶变元x，y，z；二阶变元X0，Y0，Z0；三阶变元X1，Y1，Z1；（n+2）阶变元Xn，Yn，Zn。不同阶次变元的区分相当于弗雷格关于不同层次概念的区分。事实上，罗素用“命题函项”取代了弗雷格“概念”。高阶逻辑不仅包括关于不同阶次量化的公理，也包括直谓概括公理，

还原公理是说，任意阶次的变元Xn都等价于一个二阶变元X0，

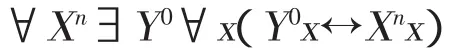
另外，无穷公理断定了无穷概念的存在，而选择公理断定了选择函数的存在。

对于标准概括公理来说，二阶量词出现在断定二阶变元存在的公式中，所以一个公式可以通过量化所有二阶变元来定义一个二阶变元的存在，也就是说，为了定义一个二阶变元，需要提及所有的二阶变元。这就是所谓的恶性循环。但是，直谓概括公理可以避免标准概括公理的恶性循环，因为包含二阶量词的公式不能断定一个二阶变元的存在，所以∃Y（y=εY∧﹁Yx）不能断定［x：x∉x］的存在，也就是说，不能断定“不属于自身”这个概念的存在。因此，直谓概括公理可以避免悖论。

弗雷格和罗素都把他们的系统表述在高阶逻辑中，但事实上，他们的系统也可以表述在一阶逻辑中。令∈是一阶语言的初始符号。在一阶逻辑中，二阶概括公理被表述为

这实际上是朴素集合论的概括公理，它是说，任意可表达公式都断定一个集合的存在。公理V被表述为

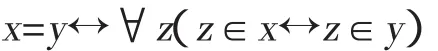
这实际上是朴素集合论的外延公理。如果把一阶变元区分为不同的种类，然后加标，即x0，y0，z0…，x1，y1，z1，…，xn，yn，zn，则可以把直谓概括公理表述为

在上述一阶版本的类型论的基础上，蒯因在《数理逻辑的新基础》中给出了一个新的系统（简记为NF）[3][4]，它包括外延公理和分层概括公理，后者是说，任意一个分层公式可以断定一个集合的存在，

一个公式φ是分层的，当且仅当，存在一个从变元到自然数的函数s，使得任给φ的原子公式x=y，s（x）=s（y），并且任给 φ 的原子公式x∈y，s（x）+1=s（y）。

在蒯因看来，如果断定集合存在的公式中不出现像x∈x或∃y（x∈y∧y∈x）这样的循环性，则罗素悖论也是可以避免的。显然，根本不存在一个函数s，使得s（x）+1=s（x）；也不存在一个函数s，使得s（x）+1=s（y）并且s（y）+1=s（x）；因此，x∈x和∃y（x∈y∧y∈x）都不是分层公式。根据分层的限制条件，并不存在不属于自身的集合。因此，分层概括公理也可以避免悖论。

二、直谓新逻辑主义的困境

受罗素类型论的启发，赫克[5]和博格斯[6]分别证明公理V与二阶直谓概括公理的一致性。二阶直谓概括公理是说，

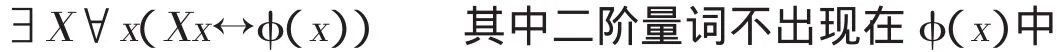
但是，赫克的直谓理论不同于博格斯的直谓理论。赫克使用了公理V的模式版本，外延算子作用于任意二阶公式的一阶变元，而博格斯使用了公理V的公理版本，外延算子作用于二阶变元，

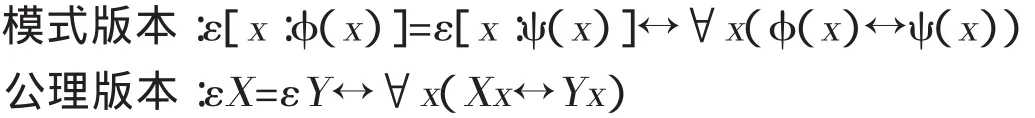
在标准概括公理的前提下，模式版本和公理版本是等价的，因为任意公式都可以断定一个概念的存在，而任意概念都有一个外延，所以任意公式都有一个外延。但是，如果概括公理受到限制，则模式版本强于公理版本：对于模式版本来说，仍然可以保证任意公式都有一个外延；而对于公理版本来说，因为不能保证任意公式都可以断定一个概念的存在，而只有概念才有外延，所以不能保证任意公式都有一个外延。

在直谓概括公理的前提下，公式∃X（x=εX∧﹁Xx）包含二阶量词，所以直谓概括公理不能断定与这个公式等价的概念的存在，即不存在“不属于自身”这个概念；又因为公理版本的公理V把外延算子作用于二阶变元，所以不能得到“不属于自身”这个概念的外延。因此，不能得到“‘不属于自身’这个概念的外延属于自身当且仅当它不属于自身”。另一方面，因为模式版本的公理V直接把外延算子作用于任意二阶公式的一阶变元，所以由它可以得到“不属于自身”这个概念的外延，即 ε［x：∃Y（y=εY∧﹁Yx）］。但是，相对于弗雷格关于属于符号的定义，直谓概括公理和模式版本的公理V不能推出如下定理[5]212，

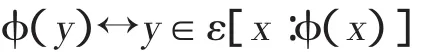
这个定理在推导罗素悖论时发挥了重要作用，如果它不成立，则不能推出罗素悖论。因此，虽然由模式版本可以得到“不属于自身”这个概念的外延，但它不会导致悖论。

两个版本的公理V都与直谓概括公理一致，但是公理版本的公理V和直谓概括公理不能推出休谟原则。为了推出休谟原则，需要把一个概念的数定义为某个特定概念的外延，即

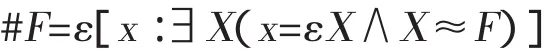
然而，公式∃X（x=εX∧X≈F）包含二阶量词∃X，其中X≈F是缩写，

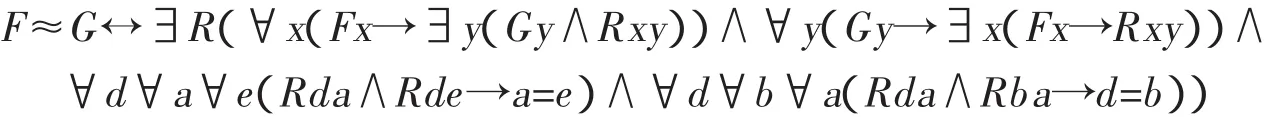
这个缩写也包含二阶量词∃R。因此，直谓概括公理不能断定与这个公式等价的概念的存在，由公理版本的公理V也不能得到这个概念的外延。虽然博格斯[6]93～104，113～117表明，不仅直谓概括公理与公理版本的公理V可以解释罗宾森算术，而且直谓概括公理和休谟原则也可以解释罗宾森算术，但是博格斯忽略了如何从公理版本的公理V推出休谟原则的过程。这显然违背了弗雷格原意。在弗雷格看来，必须首先把算术公理还原为休谟原则，然后把休谟原则还原为公理V，从而最终把算术公理还原为逻辑公理。公理版本的公理V割裂了逻辑公理与休谟原则之间的关联。

赫克[5]217～218表明，模式版本的公理V可以推出休谟原则，因为外延算子直接作用于二阶公式的一阶变元，所以概念F的数可以被定义为ε［x：∃X（x=εX∧X≈F）］。但是，模式版本的公理V不符合弗雷格关于概念和外延之间关系的基本观点，即概念是初始的，而概念的外延是派生的。弗雷格说：“在通常数学的许多专业术语中，语词‘函数’当然对应于我在此处称为函数值域的东西。但是函数是逻辑在先的，就此处所使用的这个词的意义而言。”[7]142虽然弗雷格在这里谈论的是函数，但是概念是其值为真值的函数，所以概念是函数的特例，外延是函数值域的特例。因此，关于函数及其值域的谈论也适用于概念及其外延。按照弗雷格的说法，概念与其外延之间是完全对应的，因为落在一个概念中的对象恰好是属于这个外延的对象，即∀x（Fx↔x∈εF）。但这并不意味着概念与其外延处于同等地位；相反地，概念的逻辑地位优先于外延的逻辑地位，只有在得到一个概念的前提下才能谈论这个概念的外延，也就是说，首先根据概括公理，一个公式可以断定一个概念的存在，然后根据公理版本的公理V，从这个概念得到这个概念的外延。然而，模式版本的公理V颠倒了这个顺序，它把外延算子直接作用于二阶公式的一阶变元，在不能确定与这个二阶公式等价的概念是否存在的前提下，可以直接从这个公式得到一个外延。

由此可见，直谓新弗雷格主义陷入了两难困境：一方面，模式版本的公理V可以推出休谟原则，但是模式版本颠倒了概念和外延的先后关系，不符合弗雷格关于“概念是逻辑在先”的基本观点；另一方面，公理版本的公理V符合弗雷格关于“概念是逻辑在先”的基本观点，但是公理版本不能推出休谟原则，这又违背了弗雷格“从公理V到休谟原则再到算术公理”的逻辑主义方案。

三、二阶分层概括

那么是否存在某种受限制的概括公理，使得既可以符合弗雷格关于“概念先于外延”的观点，又可以按照弗雷格关于数的定义从公理版本的公理V推出休谟原则？这是上一节留给我们的问题。本小节尝试在二阶分层概括的前提下解决这个问题。

我把由公理版本的公理V和二阶分层概括公理构成的理论称为FNF。它的语言包括：一阶变元x，y，z；一元二阶变元X，Y，Z；二元二阶变元R，S，T；连接词﹁，∨；一阶和二阶量词∀；等词=；外延算子 ε。∧，→，↔和∃可以按照通常的方式定义。它的项的形成规则包括：

如果x是一阶变元，则x是项

如果X是二阶变元，则εX是项

它的公式的形成规则包括：

如果X是二阶变元，并且t是项，则Xt是原子公式

如果t和t′是项，并且R是一元二阶变元，则t=t′和Rtt′是原子公式

如果φ和ψ是公式，则﹁φ和φ∨ψ是公式

如果x是一阶变元，φ是公式，则∀xφ是公式

如果X是一元二阶变元，R是二元二阶变元，φ是公式，则∀Xφ和∀Rφ是公式它的最重要的三条公理分别是公理版本的公理V、一元分层概括和二元分层概括：

一个公式φ是二阶分层公式，当且仅当，存在一个从变元到自然数的函数s，使得任给φ中二阶变元X，s（X）=s（εX）；任给 φ 的原子公式t=t′，s（t）=s（t′）；任给 φ 的原子公式Xt，s（t）+1=s（X），并且任给 φ 的原子公式Rtt′，s（t）=s（t′）并且s（t）+1=s（R）。

在罗素悖论的推导过程中，需要断定与公式∃X（x=εX∧﹁Xx）等价的概念的存在，由此可以断定“不属于自身”这个概念的存在，即［x：x∉x］。但是，∃X（x=εX∧Xx）不是二阶分层公式，因为不存在一个函数s使得s（x）=s（εX）=s（X）并且s（x）+1=s（X）；因此，在 FNF 中，∃X（x=εX∧﹁Xx）不能断定一个概念的存在。

事实上，可以证明FNF相对于NF是一致的。也就是说，如果NF是一致的，则FNF是一致的。换言之，如果从FNF可以推出矛盾，则从NF也可以推出矛盾。

首先，证明二元 FNF 相对于一元 FNF 是一致的。令O（x1，x2，y）是“y是序对（x1，x2）”的缩写，即

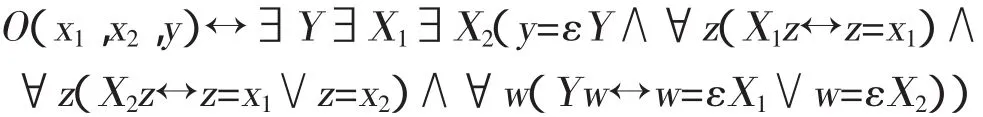
由此可以把二元FNF公式翻译为一元FNF公式。令q是从一元二阶变元和二元二阶变元到一元二阶变元的双射。然后把q扩展到从项到自身的恒等映射，也就是说，如果t是x或εX，则q（t）是t自身。在此基础上，定义从二元FNF公式到一元FNF公式的翻译函数p

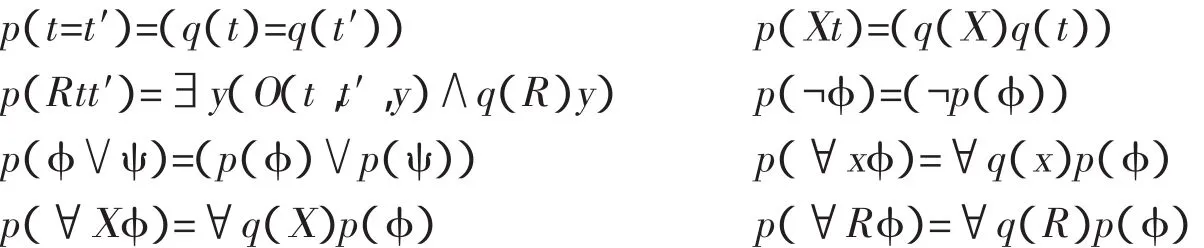
引理1：二元FNF相对于一元FNF是一致的

证明：仅仅需要证明二元分层概括经过翻译后在一元FNF中是可证的。二元分层概括经过翻译后变成

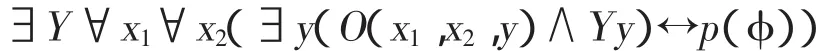
其中p（R）=Y，y是不在φ中出现的一阶变元。由一元分层概括可以得到

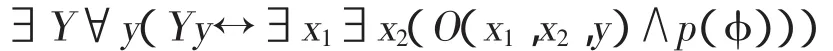
显然，如果φ分层公式，则p（φ）也是分层公式。由此可得

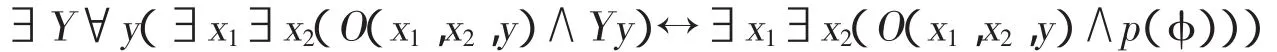
根据O（x1，x2，y）的定义，从∃x1∃x2（O（x1，x2，y）∧Yy）↔∃x1∃x2（O（x1，x2，y）∧p（φ））可以得到∀x1∀x2（O（x1，x2，y）∧Yy↔O（x1，x2，y）∧p（φ）），由此得到

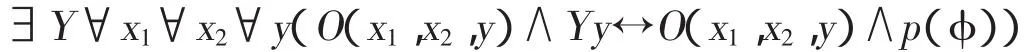
然后得到

再根据O（x1，x2，y）的定义，p（φ）↔∃y（O（x1，x2，y）∧p（φ）），因此

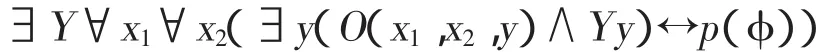
得证。□

其次，证明一元FNF相对于NF是一致的。令g是从一阶变元和一元二阶变元到一阶变元的双射，并且规定g（εX）=g（X）。在此基础上，定义从一元FNF公式到NF公式的翻译函数f：

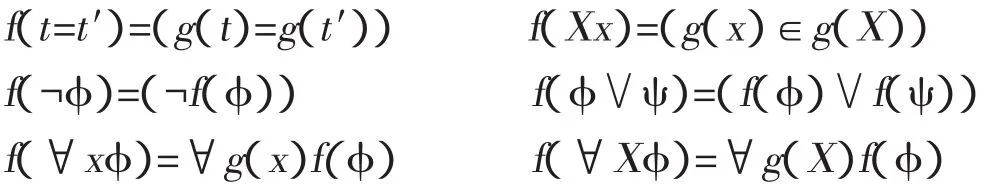
引理2：一元FNF相对于NF是一致的

证明：公理版本的公理V经过翻译后变成

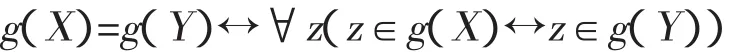
一元分层概括经过翻译后变成

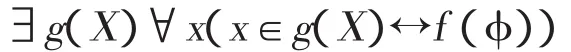
显然，这两条翻译后的公理在NF中是可证的。□

定理1：FNF相对于NF是一致的

证明：由引理1和引理2可得。□

现在我说明如何在FNF中推出休谟原则。根据二阶分层概括，可以用外延算子定义数算子，

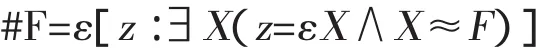
上述定义是合理的，因为公式∃X（z=εX∧X≈F）是分层的。关于这个分层公式的指派函数是

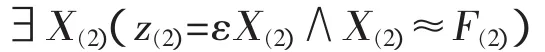
其中X（2）≈F（2）是如下公式的缩写

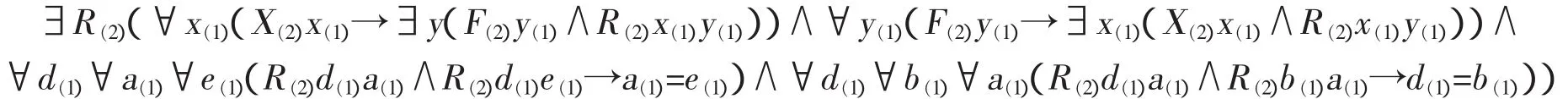
由此可以按照通常的方式从公理版本的公理V推出休谟原则。

[1]Gottlob Frege．The Basic Laws of Arithmetic：Exposition of the System[M]．Montgomery Furth Translated and Edited，with an introd．Berkeley and Los Angeles：University of California Press，1964．

[2]A．Whitehead，B．Russell．Principia Mathematica：Vol I[M]．Cambridge：Cambridge University Press，1910．

[3]Willard Quine．New Foundations for Mathematical Logic[J]．American Mathematical Monthly，1937，44．

[4]陈波．蒯因的逻辑研究[J]．湖南师范大学社会科学学报，1995，（3）．

[5]Richard Heck．The Consistency of Predictive Fragments of Frege’s Grundgesetze der Arithmetik[J]．History and Philosophy of Logic，1996，（1）．

[6]John Burgess．Fixing Frege[M]．Princeton：Princeton University Press，2005．

[7]Gottlob Frege．Collected Papers on Mathematics，Logic，and Philosophy[M]．B．McGuinness（ed．），M．Black et al．（trans．）．Oxford：Blackwell，1984．