基于S-WLLE算法和SVR的植物叶片图像识别方法
2014-08-16叶明全
杨 利,叶明全
皖南医学院计算机教研室,安徽芜湖,241002
基于S-WLLE算法和SVR的植物叶片图像识别方法
杨 利,叶明全
皖南医学院计算机教研室,安徽芜湖,241002
针对加权局部线性嵌入(Weighted Locally Linear Embedding, WLLE)算法不能充分挖掘样本类别信息以及传统流形学习算法中利用已有训练样本流形邻域关系近似得到测试样本低维嵌入的低精确性,提出了基于监督加权局部线性嵌入(Supervised Weighted Locally Linear Embedding, S-WLLE)算法和支持向量机回归(Support Vector Regression, SVR)的植物叶片图像识别方法。首先利用叶片样本监督距离代替WLLE算法中的欧式距离,对训练样本进行降维;然后学习训练样本已有数据得到SVR模型,预测测试样本的低维嵌入;最后利用最近邻分类器分别实现正负类样本以及负负类样本之间的识别。实验表明,该算法不仅提高了正负类叶片的识别精度,而且能够有效实现负负类叶片的识别。
叶片识别;监督距离;加权局部线性嵌入;降维;支持向量机回归
1 问题的提出
当前,植物叶片识别在农业信息化和生态环境保护中起着非常重要的作用,因此受到国内外学者的普遍关注,部分学者还做了一系列相关的研究,取得了很多有益的研究成果。目前,识别植物叶片的方法主要分为两种:一种提取颜色、形状和纹理作为叶片分类特征,然后利用分类器识别叶片的类别[1-8];另一种运用流形学习算法对叶片高维特征进行维数约简,在低维空间利用分类器实现叶片的识别[9-11]。由于第一种方法所用的叶片分类特征容易受到外界环境的干扰,从而影响叶片的识别率。因此,第二种方法成为当前识别叶片的主要方法。
流形学习能够有效地进行特征提取和非线性维数约简,能从高维观测数据中找到潜在的低维流形结构,并构造从高维空间到低维空间的非线性映射。局部线性嵌入(LocallyLinearEmbedding,LLE)[12]和等距特征映射(IsometricFeatureMapping,Isomap)[13]是流形学习两种具有代表性的算法,许多研究者在该算法的基础上进行了改进。文献[9]提出了一种加权局部线性嵌入(WLLE)算法,在LLE算法的代价函数中加入了样本的重要性值,有效地抑制了噪声点和样本外点,但是该算法没有运用样本的类别信息,限制了叶片图像的识别率。文献[10]提出一种新的测地距离定义,然后引入到Isomap算法中,虽然该算法能够抑制样本噪声,同时利用了样本的类别信息,但是算法复杂度较大,不容易实现。文献[11]在WLLE算法中加入了样本的类别信息,在一定程度上提高了叶片识别率,但是测试样本的低维嵌入是通过已有训练样本流形邻域关系近似得到,影响了叶片识别率的提高。同时,这些文献中仅仅实现了正负类叶片图像的识别,并没有区分负负类叶片图像之间的类别。
为此,本文提出一种基于监督加权局部线性嵌入(S-WLLE)算法和支持向量机回归(SVR)的植物叶片图像识别方法。该方法利用样本监督距离代替WLLE算法中的样本欧式距离,构成监督WLLE算法,然后利用该算法对叶片训练样本高维特征进行维数约简,得到高维训练样本的低维嵌入,再运用SVR对训练样本的高维特征和低维嵌入进行学习,得到支持向量机回归模型,预测测试样本的低维嵌入,最后在低维空间利用最近邻分类器分别实现正负类样本之间以及负负类样本之间的识别。
2 支持向量机回归(SVR)
2.1 支持向量机回归
支持向量机(Support Vector Machine,SVM)是一种常用的机器学习方法。该方法通过非线性变换,将输入样本集映射到高维特征空间,从而改善其分离状况。支持向量机回归[14]分为线性回归和非线性回归,本文主要利用支持向量机非线性回归预测高维空间样本的低维输入。
对于在原始Rn空间不可线性分离的数据集S={(x1,y1),…,(xl,yl)|xi∈Rn,yi∈R},首先通过非线性映射φ将数据集S映射到高维特征空间,使得S在特征空间H中拥有较好的线性回归特征,然后在该特征空间进行线性回归,再回归到原始Rn空间。支持向量机非线性回归优化问题的对偶形式为:
(1)
2.2 支持向量机回归算法
支持向量机回归算法[15]的具体步骤如下:
(1)给定数据集S={(x1,y1),…,(xl,yl)},xi为高维空间数据,yi是xi对应的低维输出,且i=1,2,…,l;
(2)
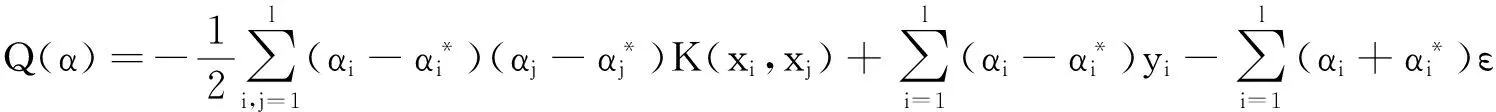
(3)
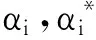
(4)
(4)对于测试样本x,选择某类型的核函数K(xi,x),构造支持向量机的非线性函数:
(5)
由此函数计算高维测试样本的低维输出。
3 监督WLLE(S-WLLE)算法
3.1 加权局部线性嵌入算法(WLLE)
由于经典流形学习算法之局部线性嵌入算法(LLE)很容易受到噪声的干扰,为了提高算法的鲁棒性,文献[9]提出一种加权局部线性嵌入算法(WLLE)。WLLE算法构建了样本的重要性值,然后将该重要性值加入到LLE算法的代价函数中。因为噪声点和样本外点的重要性值相对较小,对算法产生的影响较小,因而WLLE算法能够有效地抑制噪声点和样本外点。
WLLE算法虽然能够抑制噪声点和样本外点,但是该算法利用样本的欧式距离寻找样本近邻点和计算样本的重要性值,没有利用样本的类别信息。而样本的监督距离能够很好地挖掘样本的类别信息,有助于提高叶片图像的识别率,因此,针对WLLE算法存在的缺陷,提出一种WLLE算法和样本监督距离结合的监督WLLE算法(S-WLLE)。
3.2 监督WLLE算法(S-WLLE)3.2.1 数据点的监督距离
已有数据点(xi,ci),xi∈RD且ci是xi的类别,i=1,2,…,N,则样本点xi和xj的监督距离D(xi,xj)[16]定义为:
(6)
其中,d(xi,xj)为样本点xi和xj的欧氏距离。D(xi,xj)是关于d2(xi,xj)/β的函数,当参数α取为0.25时,坐标图如图1所示。图1中,虚线代表不同类样本之间的监督距离,实线则代表同类样本之间的监督距离,由图1可知,样本类内监督距离小于类间监督距离,而该特性能够帮助提高样本的识别率。
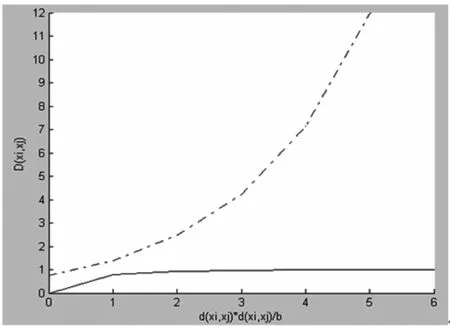
图1 d(xi,xj)关于d2(xi,xj)/β的坐标图
公式(6)中存在两个参数β和α,β的取值依赖于数据集的密度,通常情况下,将所有数据点之间欧式距离的平均值设置为参数β的值;而参数α是可调参数,取值范围为[0,0.65]。当α取0.65时,图1中两条曲线则会相交,此时d2(xi,xj)/β的值为0.38。
3.2.2S-WLLE算法
设采样得到的训练数据集X={x1,x2,…,xn}⊂RD,S-WLLE算法具体步骤为:
(1)计算训练数据集X中样本点之间的欧式距离,参数β的取值为总样本的欧式距离平均值;
(2)根据公式(6)计算数据集X中任意样本点的监督距离xi,在此基础上寻找样本的K近邻,K是预先设定的值;
(3)在已知K邻域的基础上,计算样本点xi的加权局部重构权值矩阵W,使得重构误差函数ε(W)最小,其中
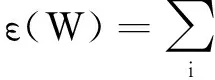
(7)
权值矩阵W由Wij构成,Wij是样本点xi与其第j个近邻点xi的权值,当xi与xj不是近邻点时,Wij为0。Wij满足约束条件
(8)
(4)计算样本点xi的重要性值Dij,其中
(9)
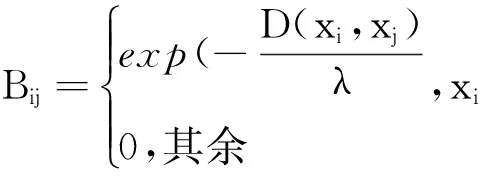
(10)
公式(10)中,λ是可调参数。
(5)保持Wij不变,计算样本点xi在低维空间的映射yi,使得加权误差函数εi(W)最小,其中
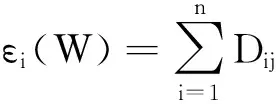
(11)
低维映射yi∈RD(d远小于D)且满足条件:
(12)
式(11)中,
M=D(I-W)T(I-W)
D=[D11,D22,…,Dnn]
(13)
(6)对稀疏矩阵M进行非稀疏对角化,得到较小的(d+1)个特征值对应的特征向量,由于第一个特征值几乎为零,故舍去。则训练样本集X对应的低维映射Y为矩阵M第2~(d+1)个非零特征值对应的特征向量。
4 基于S-WLLE算法和SVR的植物叶片图像识别方法
具体算法步骤如下:
(1)计算样本的监督距离,将其代替WLLE算法中的欧式距离形成监督WLLE算法(S-WLLE);
(2)利用S-WLLE算法对叶片训练样本高维特征进行降维,得到低维嵌入;
(3)利用SVR对叶片训练样本高维特征和低维嵌入进行学习,得到SVR训练模型;
(4)利用训练好的SVR模型预测测试样本的低维嵌入;
(5)在低维空间利用最近邻分类器分别实现正负类叶片图像之间以及负负类叶片图像之间的识别。
5 分类实验
在中国科学院合肥智能所建立的植物叶片图像数据库(http://www.intelengine.cn/data)中选取实验图片。该叶片数据库包含220种植物,共16 846幅叶片图像。实验从乌蔹莓图像中选取64幅图像,其中34幅作为正类训练样本,再从杜英、夹竹桃、东京樱花、龙牙花和含笑5种叶片图像中各选取20幅图像,选取每个物种的10幅共50幅图像作为负类训练样本,将剩余80幅图像作为测试样本。验证本文所提方法的有效性,主要做了两个实验:实验一利用主成分分析(PCA)、LLE、WLLE和S-WLLE算法对叶片图像高维特征进行降维,验证S-WLLE算法有效的聚类能力;实验二利用S-WLLE算法对叶片图像的训练样本进行降维,然后分别利用已有训练样本流形邻域关系近似计算测试样本低维嵌入和SVR预测测试样本的低维嵌入,在低维空间分别实现图2(a)与图2(b)~(f)以及图2(b)~(f)之间的识别。图2为正负类叶片图像。

图2 正负类叶片图像
从原始叶片数据库中选取的叶片图像大小不统一,对图像进行剪裁,将它们调整为128*128像素大小,然后利用小波变换将实验图像低采样成64*64像素大小,256灰度级,白色背景的灰度图像。每幅灰度图像构成了一个矩阵,再将该矩阵拉成一维的列向量[17],即训练样本和测试样本都可以用一个4096维向量表示。
5.1 聚类性能分析
实验中,每幅叶片图像可由4096维特征向量表示,由于这4096维特征向量中存在着冗余数据,可能会影响叶片识别率,因此,需要对叶片特征向量进行降维。使用主成分分析(Principal Component Analysis,PCA)[18]、LLE[12]、WLLE[9]和S-WLLE算法分别对叶片高维特征向量进行维数约简。图3为不同算法对叶片图像的聚类效果图,图中每一个点代表一幅叶片图像。
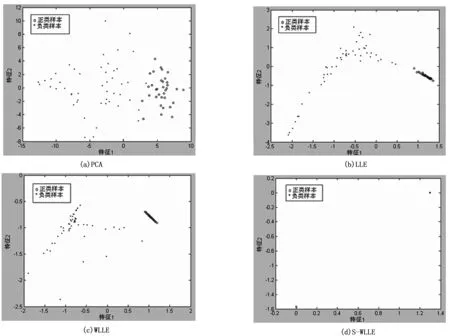
图3 不同算法聚类效果图
由图3可知,由于PCA和LLE算法容易受噪声干扰且不能利用样本的类别信息,故聚类的效果较差。WLLE算法在LLE算法的代价函数中加入了样本的重要性值,在一定程度上能够抑制样本中的噪声点和样本外点,因此聚类效果相对PCA和LLE算法稍有改善。而S-WLLE算法在抑制噪声点和样本外点干扰的同时,充分挖掘了样本的类别信息。由图3(d)可知,同类样本紧密聚在一起,不同类样本距离较远,所以聚类效果是最好的。因此,本文利用S-WLLE算法对叶片图像高维特征进行降维,再在低维空间利用分类器识别叶片图像。
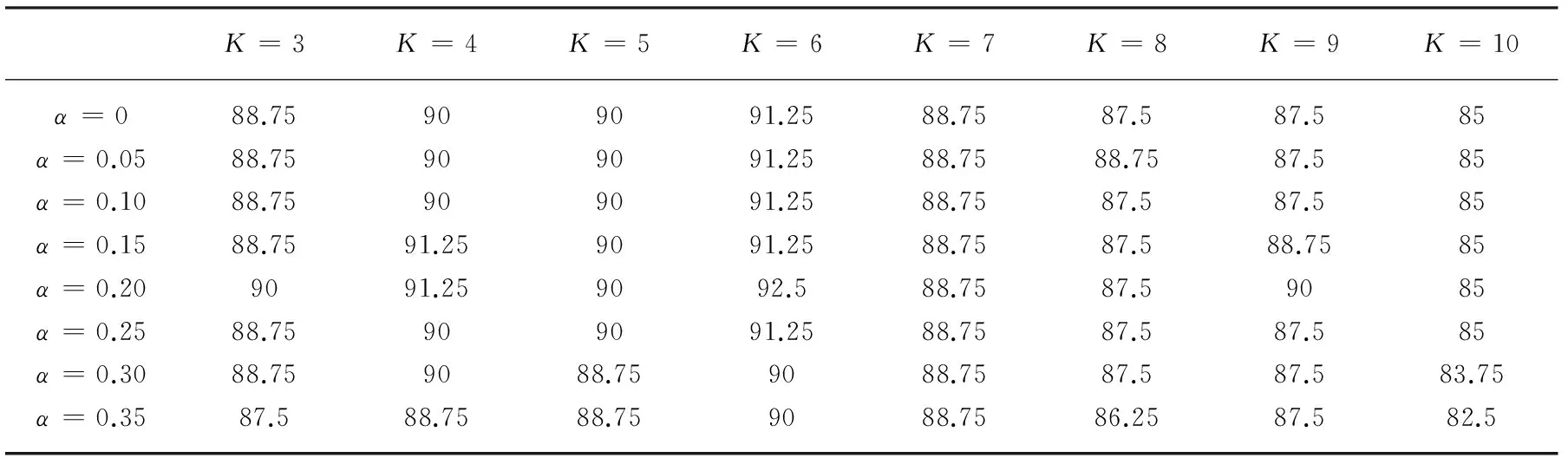
表1 不同K、α情况下叶片图像识别率 单位:%
5.2 参数选择
在叶片分类实验中,利用S-WLLE算法对叶片高维特征进行降维,而S-WLLE算法需要确定参数λ、近邻数K和参数α的取值。实验时,根据经验选取调节参数λ为100[9]。近邻数K和参数α的取值会直接影响降维算法的性能。邻域K若太小,会破坏流形的全局特性;若K太大,数据降维后就会失去原有的非线性特性。而样本的监督距离随着参数α的改变而改变。为了确定K和α值,实验固定数据集不变,K在区间[3,10]内依次取值,在区间[0,0.35]内取值,步长为0.05。实验中,利用已有训练样本流形邻域关系近似得到测试样本低维嵌入,然后在低维空间利用最近邻分类器识别叶片图像。表1为不同K、α情况下叶片图像识别率。
由表1中不同近邻数K和参数α对应得到的叶片识别率可知,利用S-WLLE算法对叶片高维特征进行降维,在低维空间利用最近邻分类器识别叶片图像,综合考虑K和α,当K取6,α取0.2时,得到的叶片识别率最高。因此,实验一就采用此最优参数组合。
5.3 实验结果
为了验证本文方法能够有效提高叶片图像的识别率,本文做了两个实验。实验一利用算法PCA、LLE、WLLE和S-WLLE分别对叶片图像高维特征进行降维。对于S-WLLE算法,利用已有训练样本流形邻域关系近似得到测试样本低维嵌入,然后在低维空间利用最近邻分类器识别正负类叶片图像。每个实验重复20次,实验中训练样本和测试样本在样本集中随机抽取。表2为20次实验不同算法的叶片最佳识别率和平均识别率。
由表2叶片图像识别结果可知,由于监督算法S-WLLE充分挖掘了样本的类别信息,因此利用该算法得到的叶片图像识别率要明显高于其他三种算法。

表2 不同算法的叶片图像识别结果 单位:%
实验二利用S-WLLE算法对叶片训练样本高维特征进行降维,然后分别利用已有训练样本流形邻域关系近似计算测试样本低维嵌入和利用SVR预测测试样本的低维嵌入这两种方法计算测试样本的低维嵌入。实验中SVR选择径向基(RBF)函数作为核函数,其他参数选择系统默认值。在低维空间利用最近邻分类器分别对叶片正负类样本以及负负类样本进行识别。每组实验重复20次,每次实验随机产生训练样本和测试样本,实验中K取3,α取0.20,以20次实验的最佳识别率和平均识别率作为叶片图像识别结果。表3为20次实验叶片图像的最佳识别率和平均识别率。
由表3可知,利用SVR预测测试样本的低维嵌入得到的叶片图像识别率要明显高于传统方法。同时利用本文方法能够有效地区分叶片负类样本。

表3 叶片图像的识别结果 单位:%
6 结束语
在叶片图像识别方法中,非监督流形学习算法WLLE没有利用到样本的类别信息,同时测试样本的低维嵌入通过已有训练样本流形邻域关系近似得到,限制了叶片图像的识别精度。针对这两个缺陷,本文提出了一种基于S-WLLE算法和SVR的植物叶片图像识别方法,利用样本监督距离代替WLLE算法中的样本欧式距离,从而充分挖掘样本的类别信息;同时,利用SVR对训练样本的高维特征和低维嵌入进行学习得到支持向量机回归模型,精确预测测试样本的低维嵌入。实验结果表明,本文提出的叶片图像识别方法不仅提高了叶片图像正负类样本的识别率,而且能够有效区分叶片图像负负类样本。
[1]Du J,Huang D,Wang X,et al.Shape recognition based on radial basis probabilistic neural network and application to plant species identification[M].Berlin:Springer-Verlag,2005:281-285
[2]Neto J C,Meyer G E,Jones D D,et al.Plant species identification using elliptic Fourier leaf shape analysis[J].Computers and Electronics in Agriculture,2006,50(2):121-134
[3]Lee C L,Chen S Y.Classification of leaf images[J].International Journal of Imaging Systems and Technology,2006,16(1):15-23
[4]Neto J C,Meyer G E,Jones D D,et al.Plant species identification using Elliptic Fourier leaf shape analysis[J].Computers and Electronics in Agriculture,2006,50(2):121-134
[5]杜吉祥,汪增福.基于径向基概率神经网络的植物叶片自动识别方法[J].模式识别与人工智能,2008,21(2):206-213
[6]Bruno O M,de Oliveira Plotze R,Falvo M,et al.Fractal dimension applied to plant identification[J].Inform Sci,2008,178(12):2722-2733
[7]孙永新.基于多尺度形状分析的叶形识别系统[J].计算机应用,2009,29(6):1707-1710
[8]张宁,刘文萍.基于图像分析的植物叶片识别技术综述[J].计算机应用研究,2011,28(11):4001-4007
[9]张善文,王献峰.基于加权局部线性嵌入的植物叶片图像识别方法[J].农业工程学报,2011,27(12):141-145
[10]张善文,黄德双.一种鲁棒的监督流形学习算法及其在植物叶片分类中的应用[J].模式识别与人工智能,2010,23(6):836-841
[11]阎庆,梁栋,张晶晶.基于Fisher变换的植物叶片图像识别监督LLE算法[J].农业机械学报,2012,43(9):179-183
[12]Roweis S T,Saul L K.Nonlinear dimensionality reduction by locally linear embedding[J].Science,2000,290:2323-2326
[13]Tenenbaum J B,De Silva V,Langford J C.A global geometric framework for nonlinear dimensionality reduction[J].Science,2000,290:2319-2323
[14]徐红敏,王海英,梁瑾,等.支持向量机回归算法及其应用[J].北京石油化工学院学报,2010,18(1):62-66
[15]力琼.支持向量机回归在传染病预测中的应用研究[D].江苏:苏州大学苏州大学计算机科学与技术学院,2010:28
[16]Geng X,Zhan D C,Zhou Z H.Supervised nonlinear dimensionality reduction for visualization and classification[J].IEEE Transactions on SMC B,2005,35(6):1098-1107
[17]Hu Rong-xiang,Wei Jia,Huang De-shuang,et al.Maximum margin criterion with tensor representation[J].Neurocompution,2010,73(10/12):1541-1549
[18]李慧,祁力钧,张建华,等.基于PCA-SVM的棉花出苗期杂草类型识别[J].农业机械学报,2011,43(9):184-189
(责任编辑:汪材印)
宿州学院“国家级工程技术研究中心”获准立项
日前,国家科技部发文公布了《关于2014年度国家工程技术研究中心立项的通知》,宿州学院与皖北煤电集团、中国矿业大学(北京)共同组建申报的“国家煤矿水害防治工程技术研究中心(编号:2014FU125Q06)”获批立项。
An Exploration of Recognition Method of Plant Leaves Based on S-WLLE Algorithm and SVR
YANG Li,YE Ming-quan
Computer Teaching and Research Section,Wannan Medical College, Wuhu Anhui 241002, China
Weighted locally linear embedding algorithm can't mine adeqtely sample category information,and the low accuracy of traditional manifold learning algorithm uses existed manifold neighborhood of training sample to obtain test sample wity low embedding accuracy.this paper proposed a recognition method of plant leaves based on supervised weighted locally linear embedding algorithm and support vector regression.First,it used supervised distance to replace sample Euclidean distance in WLLE to reduce training sample dimensions. Then, it learned the training sample data to form SVR model to predict test sample's low dimension embedding.Finally,it recognized leaves between positive and negative and between negative and negative by the nearest classifier. The experimental results show that the proposed method not only improves the leaves classification accuracy between positive and negative sort of the leaves but also distinguishes two negative sorts of the leaves effectively.
leaves recognition;supervised distance;weighted locally linear embedding;dimension reducing;support vector regression
10.3969/j.issn.1673-2006.2014.11.021
2014-05-04
国家自然科学基金面上项目“网络环境下数字图像可信性度量理论与方法研究”(61272540);安徽省高校省级自然科学研究重点项目“面向肿瘤基因表达数据的特征选择与集成分类研究”(KJ2014A266)。
杨利(1984-),安徽池州人,硕士,助教,主要研究方向:模式识别、信息检索。
TP391.41
A
1673-2006(2014)11-0069-06
