强共归纳数据类型上的Comonadic共递归*

苏锦钿 余珊珊

(1.华南理工大学 计算机科学与工程学院，广东 广州 510006;2.广东药学院 医药信息工程学院，广东 广州 510006)

在范畴论的视角下，共归纳数据类型［1-2］可看成是某个共递归类型等式上的最大固定点，并且可抽象地描述为某个共代数函子的终结共代数［3-4］.由共归纳数据类型所对应的终结共代数及其终结性可得到一种重要的共递归，称为unfold［1-3］或atamorphism［4］，并可进一步得到其他的共递归，如原始共递归或Course-of-Value 共递归［5］等.这些共递归操作满足一系列的共代数计算律，在基于行为关系的函数定义和程序推理及转换过程中具有重要的作用［6-7］.

笔者在前期工作中分别研究了共归纳数据类型上的共递归操作及其计算律，以及它们在计算机科学中的应用［3，8］，并从双代数的角度探讨了归纳与共归纳数据类型、fold 与unfold 之间的关系［9］，但这些工作均没有涉及到共归纳数据类型的强终结性及带参数的共递归操作.作为范畴论编程语言Charity的基础，强数据类型是指满足一些额外性质的数据类型［10］.目前对强数据类型的研究主要以强归纳数据类型［11-12］为主，即归纳数据类型所对应的初始代数在参数下是初始的.Pardo［13-14］利用笛卡尔封闭范畴上的初始代数是强初始的性质，给出了强归纳数据类型上的带固定参数及累积参数的递归操作pfold 和afold 的定义，并结合积Comonad 对它们进行结构化描述.但Pardo 的研究主要针对强归纳数据类型及带参数的递归操作，不适合直接应用于共归纳数据类型.Cockett 等［15］虽然提出了强共归纳数据类型的概念，但没有给出具体的证明，也没有分析强共归纳数据类型上的各种计算律.

因此，在上述研究的基础上，文中给出了强共归纳数据类型的定义及一种带固定参数的共递归操作，称为punfold;并结合Comonadic 共递归给出了unfold 和punfold 的一种统一的结构化描述，同时分析了punfold 上的各种计算律.

1 相关理论

1.1 共代数和多项式函子

定义1 给定笛卡尔封闭范畴C 和C 上的自函子F:C →C，一个F-共代数定义为一个二元组(X，αX:X→FX)，其中X 称为该F-共代数的载体，αX称为该F-共代数的基调.任意两个F-共代数(X，αX:X→FX)和(Y，αY:Y→FY)间的同态射f:(X，αX)→(Y，αY)，是载体集上的射f:X →Y，且满足等式αXf=FfαY.

若函子F 存在终结共代数，记为(νF，outF)，则对于任意一个F-共代数(X，αX)，总是存在从(X，αX)到(νF，outF)的唯一同态射unfoldF(αX):X→νF.unfoldF(αX)是由基调αX所确定的一个共递归，通常称为unfold［1-3］或atamorphism［4］.

例1 参数化数组List［A］(记为A*，其中A 为某个已知的数据类型)可看成是函子L=1 +A ×X的终结共代数上的载体.数组A*上的基调包括一个谓词操作isnil:X→1 +1(用于判断数组是否为空)，以及两个观察操作head:X→A 和tail:X→X(用于给出数组的当前元素及剩余部分).A*及其上的操作可表示为一个终结共代数结构:

(A*，outL=〈isnil，head，tail〉:A*→1 +A ×A*)，其中outL定义为(1 +〈head，tail〉)isnil?.

为了保证共代数函子存在相应的终结共代数，只考虑以下的有限扩展多项式函子［10］.

定义2 给定一个范畴C，称自函子F:C→C 为有限扩展多项式函子，当且仅当F 是由以下的函子类型归纳构造而成:

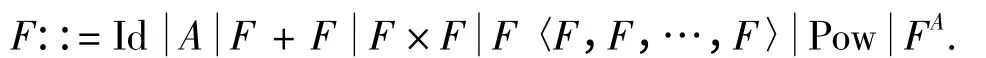
其中:Id 为标识函子;A 为A 上的常量函子;F+F 和F×F 分别为函子间的共积和积;F〈F，F，…，F〉(记为F〈Fi〉)为F:C→Cn与其他有限扩展多项式函子F1，F2，…，Fn的组合，可看成是映射为X →F(F1X，F2X，…，FnX)的函子，且F1，F2，…，Fn均具有相同的元数;Pow 为有限幂集函子;FA为指数函子，表示常量A 与函子F 间的一个函数关系.

根据文献［16］中的定理10.6，上述函子均为有限的，因此存在着对应的终结共代数.例如，函子F(－)=1 +A×－的终结共代数为(A*，〈isnil，〈head，tail〉〉:A*→1 +A×A*)，给出了数组上所有可观察行为的典型实现.函子F(－)=A ×－的终结共代数为(A∞，〈value，next〉:A∞→A∞×X)，给出了所有无限流上的可观察输出值.

定义3 称函子F:C→C 为强函子，当且仅当存在一个自然转换:FX×Y→F(X ×Y)，满足以下等式:

其中assX，Y，Z=〈〈fst，fstsnd〉，sndsnd〉:X ×(Y ×Z)→(X×Y)×Z 表示结合律的自然同构射称为函子F 的右强度，fst:X ×Y→X 和snd:X ×Y→Y分别为笛卡儿积上的左和右投影函数.

对于笛卡尔封闭范畴来说，上述有限扩展多项式函子都是强函子［17］，并且存在以下的射:

(1)自然同构射dist:(X+Y)×Z→X×Z+Y×Z;

(2)applyA，X:XA×A→X，且对于任意一个射f:X×A→Y，都有一个唯一的射curry(f):X→YA与之对应，使得f=applyA，Xcurry(f)×IdA.

对于指数函子FA，存在转换:(FX)A→FXA，且可以归纳地定义如下:

其中G 为范畴C 上的有限扩展多项函子，inl－1:X +Y→X 和inr－1:X +Y→Y 分别为左注入射(inl:X→X+Y)和右注入射(inr:Y→X+Y)的逆，表示共积到其左右分量的射.

1.2 Comonads

定义4 范畴C 上的Comonad 为一个三元组(D，ε，－D)，称为coKleisli 三元组，其中为C 中对象间的函数关系，使得对于有εX:DX→X，对于f:DX→Y，有fD:DX→DY，且满足以下等式:

(1)(εX)D=IdDX;

(2)对于射f:DX→Y，有fD;εY=f;

(3)对于任意两个射f:DX→Y 和g:DY→Z，有fD;gD=(fD;g)D.

若将DX 看成是X 上的某种计算类型，D 为该计算的上下文环境，那么εX:DX→X 表示取出该计算环境中的值，fD:DX→DY 表示将f 扩展为包含上下文环境的计算.例如，对于标识Comonad D=Id，f:DX→Y 表示一般的确定性函数f:X→Y;对于积Comonad(或称流Comonad［18］)D=Id ×A，f:DX→Y表示一个带参数且类型为A 的确定性函数f:X ×A→Y，fD=〈f，snd〉:DX→DY 表示把计算源中的参数复制到输出中.

定义5 给定范畴C 中的一个coKleisli 三元组(D，ε，–D)，对应的coKleisli 范畴CD定义如下:

(1)CD中的对象与C 中的对象相同;

(2)CD中任意对象X 到Y 的射为C 中对应的射f:DX→Y;

(3)CD中任意对象X 上的标识射为εX:DX→X;

(4)CD中射f:DX→Y 与g:DY→Z 的组合为gfD:DX→Z.

为了区别于一般的射，将coKleisli 范畴中每一个形如f:DX→Y 的射称为Comonadic 射.

定义6 给定范畴C 上的一个Comonad(D，ε，–D)和自函子F:C→C，则D 对F 的分配律为自然转换:DFFD，且满足以下等式:

(1)FεXX=εFX;

(2)F(IdDX)DX=DXDX(IdDFX)D.

对于函子F:C→C 及其上的Comonad(D，ε，－D)，若存在分配律:DFFD，则可定义函子:CD→CD，将对象X 映射为它自身F X=X，将Comonadic 射f:DX →Y 映射为F f=FfX:DFX→FY，将f:DX→Y和g:DY→Z 的组合gfD映射为(gfD)=(f )D:DX→FZ.F 可看成是函子F 在Comonad(D，ε，–D)及分配律:DFFD 下的一个函子化提升，称为F 的Comonadic 提升或扩展.

将形如(X，φX:DX→FX)的结构称为Comonadic F-共代数，记为FD-共代数.任意两个FD-共代数(X，φX:DX→FX)和(Y，φY:DY→FY)间的FD-共代数同态射f:(X，φX)→(Y，φY)为Comonadic 射f:DX→Y，且 满 足YfD= F fφX.若 射f:X →Y 满 足Df=FfφX，则称f 为(X，φX)和(Y，φY)间的纯FD-共代数同态射.

每个Comonad 下的所有FD-共代数及其同态射可构成一个范畴，记为CDF.例如，对于标识Comonad D=Id 和积Comonad D=Id ×A，CDF分别记为CIdF和若(νF，out'F:DνF→FνF)是范畴中的终结对象，那么总是存在从中任意一个对象(X，φX:DX →FX)到(νF，out'F)的唯一射unfoldF，D(φX):DX→νF，并且unfoldF，D(φX)为一个FD-共代数同态射.为了区别于一般的unfold，将形如coKleisli 范畴中的unfoldF，D(φX)射称为Comonadic unfold.

2 强共归纳数据类型

给定范畴C 及其上的一个Comonad(D，ε，－D)，可定义一个从C 到CD的提升函子(－)#:C→CD，将范畴C 中的每一个对象X 映射为它本身(X)#=X，将C 中的每一个射f:X→Y 映射为f#=fεX:DX→Y，称f#是f 在(D，ε，－D)下的一个Comonadic 提升.

命题1 对于任意的Comonad(D，ε，－D)，每一个F-共代数(X，αX:X→FX)满足

证明 由(－)#和(－)D的定义可知命题1 成立.

证毕.

定义7 称强函子F 的终结共代数(νF，outF)是强终结的，当且仅当对于对象A，提升fst:νF×A→FνF 是范畴中的一个终结对象.

命题2 笛卡尔封闭范畴上的终结共代数是强终结的.

证明 给定积Comonad D=Id ×A 及分配律 :DFFD，对于任意一个FD-共代数(X，φX:X ×A→FX)，可构造射h=applyA，DX:(X ×A)A×A→F(X×A)和对应的curry(h):(X ×A)A→(F(X ×A))A.再由可得到一个F-共代数curry(h):(X×A)A→F(X×A)A.

即图1 中的左半部分满足图表交换条件.再由终结共代数的终结性可知(3)也满足交换条件，其中f=unfoldF(k).因此，整个图表满足交换条件.知，对任意一个射f:(X ×A)A×A→νF，都存在另一

图1 终结共代数的强终结性Fig.1 Strong finality of final coalgebras

由X×A 与(X ×A)A×A 间的一一对应关系可个射f'= f〈curry(fst)，snd〉:X×A→νF 与之对应，因此〈f，snd〉〈curry(fst)，snd〉=〈f〈curry(fst)，snd〉，snd〉=〈f'，snd〉.再由F f〈F curry(fst)，snd〉=F〈f〈curry(fst)，snd〉〉=F f'可知，f'是唯一射，且满足:

因此，outF是强终结的，且有

证毕.

利用命题2 可以给出强归纳数据类型的定义.

定义8 称一个共归纳数据类型是强共归纳类型，当且仅当该共归纳数据类型所对应的终结共代数是强终结的.

由outF是同构射的性质，容易验证也是一个同构射，因此可以作为范畴的一个终结FD-共代数，而任意一个FD-共代数(X，φX)到(νF)的唯一同态射f:DX→νF，实际上给出了一种带固定参数的共递归计算，称为punfold.

图2 punfold 的定义Fig.2 Definition of punfold

每一个punfoldF(φX):X×A→νF 可以看成是:共递归的计算源包含了参数类型为A 的元素，并且该参数值在计算过程中保持不变.容易验证存在等式

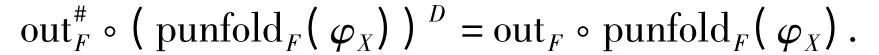
图3 punfold 的Comonadic 表示Fig.3 Comonadic expressions of punfold

命题3 每一个punfold 等价于积Comonad D=Id×A 下的Comonadic unfold 射.

证明 由定义9 及积Comonad 的定义可得

证毕.

例2 函数lmult:Nat*×Nat→Nat*将自然数数组Nat*中的每一个元素都分别乘以某个给定的自然数，即对于a，xNat 和xsNat*，lmult 定义为

lmult(［］，a)=［］，

lmult(x:xs，a)=(x×a):lmult(xs，a).

显然，lmult 可定义为一个punfold:

lmult=punfoldL(mlist):Nat*×Nat→Nat*.

或者定义为积Comonad D=Id×Nat 下的Comonadic unfold:

unfoldF，Id×Nat(mlist):Nat*×Nat→Nat*.

其中基调mlist=〈m_isnil，m_head，m_tail〉:Nat*×Nat→1 +Nat ×Nat*中的操作m_isnil:Nat*×Nat→1 + 1、m_head:Nat*×Nat →Nat 和m_tail:Nat*×Nat→Nat*分别定义为

命题4 每一个unfold 都可以看成是计算过程中不使用参数的punfold，或者是任意范畴中的一个纯FD-共代数同态射.

证明 由定义9 可知，每一个unfoldF(αX):X→νF 实际上相当于在计算过程中不使用参数A 的punfold，并且在积Comonad D=Id ×A 下的Comonadic提升满足(unfoldF(αX))#=punfoldF().显然，对任意Comonads 下的范畴，unfoldF(αX)都是从(X)到(νF，)的一个纯FD-共代数同态射.

证毕.

3 punfold 上的计算律

定律1(标识律) 给定积Comonad D=Id ×A和分配律 :DFFD，强函子F 上的终结共代数(νF，outF)满足punfoldF()=ενF.

证明 由积Comonad 下的Comonadic 提升和定义9 可知，FενF()D=(ενF)D，即ενF为一个punfold，再由其唯一性知punfoldF)=ενF.

证毕.

定律2(消去律) 给定积Comonad D=Id ×A和分配律:DFFD，punfold 满足:

证明 由定义9 和命题3 可得

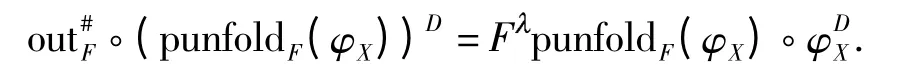
证毕.

定律3(FD-共代数同态射融合律) 给定积Comonad D= Id×A 和分配律 :DFFD，一个punfold与一个FD-共代数同态射的组合仍是一个punfold，即

证明 由前提可知，图4 中的(1)和(2)满足图表交换条件.因此，整个图表也满足交换条件.

证毕.

定律3 表示范畴CFId×A中的Comonadic unfold与一个Comonadic 射间的coKleisli 组合仍是一个Comonadic unfold.

图4 punfold 与FD-共代数同态射间的组合定律Fig.4 Fusion law for punfold and FD-coalgebraic homomorphism

定律4(纯FD-共代数同态射融合律) 给定积Comonad D= Id×A 和分配律 :DFFD，一个punfold与一个纯FD-共代数同态射的组合仍是一个punfold:

证毕.

定律4 表明，在范畴CId×AF中的Comonadic unfold与一个纯FD-共代数同态射的组合仍是一个Comonadic unfold.

例3 函数odd:Nat*→Nat*是积Comonad D=Id×Nat 下从(Nat*，olist=〈o_isnil，o_head，o_tail〉)到(Nat*，mlist=〈m_isnil，m_head，m_tail〉)的纯FD-共代数同态射，用于取出Nat*中奇数位上的元素.基调olist=(1 +〈o_head，o_tail〉)o_isnil?中的操作分别定义为

o_isnil(xs，a)=isnil(xs)，

o_head(xs，a)=head(xs)×a，

o_tail(xs，a)=tail(tail(xs)).

根据定律4 可将函数odd 与例子2 中的函数lmult 合并为一个新的punfold，即

定律5(punfold 融合律) 给定积Comonad D=Id×A 和分配律:DFFD，若存在一个自然转换子T:(DX →FX)→(DX →GX)，将 每 个FD-共 代 数(X，φX)映射为一个GD-共代数(X，T(φX))，将每个FD-共代数同态射f:(X，φX)→(Y，φY)映射为对应的GD-共代数同态射，则两个punfold punfoldF(φX)与punfoldG(T(out#F))之间的组合仍是一个punfold:punfoldG(T))punfoldF(φX)=punfoldG(T(φX)).

证明 令g=punfoldF(φX)，f=punfoldG(T)).

由前提及自然转换子保持同态射的性质可知，图5中的(1)和(2)均满足交换条件，且有G g(G f)D=G (gfD).再由终结共代数的强终结性及唯一性可知，gfD为一个punfold，即

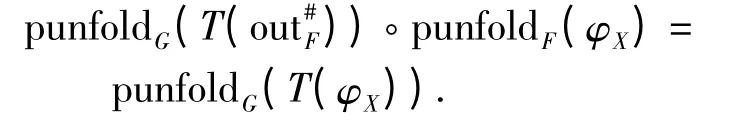
证毕.

图5 punfold 间的融合律Fig.5 Fusion law for punfold

定律6(punfold-unfold 融合律) 若存在一个自然转换子S:(X→FX)→(DX→GX)，将每个F-共代数(X，αX:X→FX)映射为积Comonad D=Id ×A 下的GD-共代数(X，S(αX):DX→GX)，将每个F-共代数同态射f:(X，αX)→(Y，αY)映射为对应的纯GD-共代数同态射，则一个punfold f=punfoldF(φX)与一个unfold g=unfoldF(αX)的组合仍是一个punfold，即

punfoldG(S(outF))unfoldF(αX)×IdA=punfoldG(S(αX)).

证明 由前提和定律4 可容易得到

punfoldG(S(outF))unfoldF(αX)×IdA=punfoldG(S(αX)).

证毕.

利用上述各种融合律可以消去punfold 在计算过程中所产生的中间数据，从而简化程序结构.

4 结语

目前，强归纳数据类型已经成为一些函数式程序语言(如Charity)的基础.而强共归纳数据类型使得定义在共归纳数据类型上的共递归计算具备管理和操纵参数的能力，因此可以在计算源中包含额外的参数用于作为共递归计算的输入，这不仅有助于提高共递归对动态行为的描述能力，可利用Comonads 与Monads 间的对偶性，将coKleisli 范畴对上下文依赖计算的结构化描述与Kleisli 范畴对副作用计算的结构化描述有机地融合起来，而且有助于促进强共归纳数据类型和Comonads 在各种数据流编程语言(如Lucid、Lustre 或Lucide Synchrone等)、并行计算及其他更复杂的计算内涵语义和上下文依赖计算研究中的应用.

今后将继续研究如何利用双代数将强归纳数据类型和强共归纳数据类型统一起来，给出强抽象数据类型的定义及带固定参数和累积参数的递归及共递归，并探讨相应的计算律.

［1］Hutton G.Fold and unfold for program semantics［C］∥Proceedings of the 3rd ACM SIGPLAN International Conference on Functional Programming.New York:ACM，1998:280-288.

［2］Gibbons J，Jones G.The under-appreciated unfold［C］∥Proceedings of the 3rd ACM SIGPLAN International Conference on Functional Programming.New York:ACM，1998:273-279.

［3］苏锦钿，余珊珊.共归纳数据类型上的共递归操作及其计算定律［J］.华南理工大学学报:自然科学版，2011，38(10):90-95.Su Jin-dian，Yu Shan-shan.Corecursion operations and its calculation laws on coinductive data types［J］.Journal of South China University of Technology:Natural Science Edition，2011，38(10):90-95.

［4］Meijer E，Fokkinga M，Paterson R.Functional programming with bananas，lenses，envelopes and barbed wire［M］∥Functional Programming Languages and Computer Architecture.Berlin:Springer-Verlag，1991:215-240.

［5］Uustalu T，Vene V.Primitive (co)recursion and courseof-value (co)iteration，categorically［J］.Informatica，1999，10(1):5-26.

［6］Hinze R.Reasoning about codata ［C］∥Proceedings of the Third Summer School Conference on Central European Functional Programming School.Berlin:Springer-Verlag，2010:42-93.

［7］Vene V，Uustalu T.Functional programming with apomorphism(corecursion)［J］.Proceedings of the Estonian Academy of Science:Physics，Mathematics，1998，47(3):147-161.

［8］苏锦钿，余珊珊.程序语言中的共归纳数据类型及其应用［J］.计算机科学，2011，38(11):114-118.Su Jin-dian，Yu Shan-shan.Coinductive data types and their applications in programming languages［J］.Computer Science，2011，38(11):114-118.

［9］苏锦钿，余珊珊.抽象数据类型的双代数结构［J］.华南理工大学学报:自然科学版，2011，39(12):1-7.Su Jin-dian，Yu Shan-shan.Bialgebraic structure of abstract data types［J］.Journal of South China University of Technology:Natural Science Edition，2011，39(12):1-7.

［10］Pardo A.A calculational approach to strong datatypes［R］.Norway:Department of Informatics，University of Oslo，1996.

［11］Greiner J.Programming with inductive and co-inductive types［R］.Pittsburgh:School of Computer Science，Carnegie-Mellon University，1992.

［12］Geuvers H.Inductive and coinductive types with iteration and recursion ［C］∥Proceedings of the Workshop on Types for Proofs and Programs.Bastad:Chalmers University，1992:193-217.

［13］Pardo A.Towards merging recursion and Comonads［C］∥Proceedings of the 2nd Workshop on Generic Programming.Utrecht:University of Utrecht，2000:50-68.

［14］Pardo A.Generic accumulations［C］∥Proceedings of IFIP TC2/WG2.1 Working Conference on Generic Programming.New York:ACM，2003:49-78.

［15］Cockett J R B，Spencer D.Strong categorical datatypes I［C］∥Proceedings of International Summer Category Theory Meeting 1991.Montreal:American Mathematical Society，1991:141-169.

［16］Rutten J J M M.Universal coalgebra:a theory of systems［J］.Theoretical Computer Science，2000，249(1):3-80.

［17］Kock A.Strong functors and monoidal Monads ［J］.Archiv der Mathematik，1972，23(1):113-120.

［18］Uustalu T，Vene V.Signals and Comonads［J］.Journal of Universal Computer Science，2005，22(7):1310-1326.