SoS 滤波器及其在工业超声波成像中的应用*

戴光智 韩国强 林伟毅 欧阳显跃

(1.华南理工大学 计算机科学与工程学院，广东 广州 510006;2.华南理工大学 自动化科学与工程学院，广东 广州 510640;3.湖南大学 嵌入式与网络计算湖南省重点实验室，湖南 长沙 410082)

Donoho 和Candès 等［1-4］提出的采样与压缩同步进行的压缩感知(CS)理论与传统的“先采样后压缩”不同，它采用“边采样边压缩”的方法.CS 理论指出，只要信号是稀疏的，那么信号的采样频率可以远远低于信号频谱中最高频率的2 倍而不影响信号的精确重建.将CS 理论应用于工业超声波成像系统中，可以有效地减少采样点和采样频率.目前，国内外将CS 应用于超声领域的研究［5-13］主要集中在医用超声方面，在工业超声方面的研究很少.有限新息率(FRI)模型是传统采样理论与CS 相结合的信号采集方法［14］.具有FRI 性质的信号可以由各个短脉冲信号的延时和幅度进行完备的表示，因此可以有效地减少采样数据和采样频率.工业超声波成像系统的反射信号可以看成一系列不同延时和幅度的高斯脉冲信号的叠加，因此，工业超声波成像系统的反射信号具有FRI 性质，可以利用FRI 模型中的采样方法进行信号采样和重建.但现有的FRI 信号采集方法对高频信号进行采样时很不稳定.通常，工业超声波成像系统的反射信号频率很高，导致现有的FRI 模型并不能很好地应用于工业超声波成像系统中.因此，文中研究能够采集高频信号的FRI 信号采集方法，对CS 理论在工业超声波成像系统中的应用具有重大的意义.

为有效地减少采样数据和采样频率，文中提出了一种适用于工业超声信号处理的新型FRI 采集方法——辛格函数之和(SoS)滤波器法，推导了这种采集方法应具备的条件，给出了SoS 滤波器的构造方式，并利用SoS 滤波器对一维超声波成像原始数据进行处理，最后通过仿真实验验证了该方法的可行性.

1 压缩感知理论和FRI 模型

1.1 压缩感知理论

CS 理论指出，当信号满足稀疏或可压缩性时，可以采集少量观测信号，然后通过求解一个优化问题准确重建原始信号.由信号理论可知，时域信号X(XRn×1)能够用一组基Ψ(Ψ=(ψ1，ψ2，…，ψn))线性表示，即

式中，α 为n 维系数向量，α=(α1，α2，…，αn).如果式(1)中系数αi仅有k 个非0，则称信号X 是稀疏的，称Ψ 为信号X 的稀疏基或稀疏字典.如果对X的测量也是在时域上进行的，则有

其中Θ(Θ=ΦΨ)为m×n 阶矩阵.由于式(3)中的α 是k 稀疏的，且k ＜m ＜n，故α 可以通过式(4)的最优化问题获得，即

可以通过基于l1范数的最优化方法(如贝叶斯方法)求解目标信号α，但其前提是测量矩阵必须满足RIP 性质.

1.2 FRI 模型

假设得到如下一个周期为 的无限周期信号:

式中，h(t)为形状和周期已知的脉冲，tl和al(l=1，2，…，L)分别为未知的延时和幅度，L 为一个周期内短脉冲的个数.假设一个周期内得到M 个连续的傅里叶系数，则x(t)的傅里叶变换为

选择M个连续的整数，使得矩阵H 是可逆的，定义y=H-1x ，则有

式中，V为Vandermonde 矩阵，因此只要L ≤M，则V 是列满秩的.

将方程组(8)进行重写，有

由式(7)-(9)可知，一旦得到傅里叶系数向量x，并保证2L≤M，就可以根据方程组(8)解出tl和al(l= 1，2，…，L).文中采用零化滤波重建算法［15］求解方程组(8)，当然也可以使用其他的方法，如矩阵束算法［16］.

2 FRI 滤波器组及SoS 滤波器

2.1 FRI 滤波器组

傅里叶系数的采集是稀疏重建成像的关键.在时间域上对FRI 信号x(t)进行采样(采样函数为s*())，可以得到M(2L≤M)个傅里叶系数，能实现此功能的方法的集合称为FRI 滤波器组.假设待采样信号为周期信号，其采样框架如图1 所示.

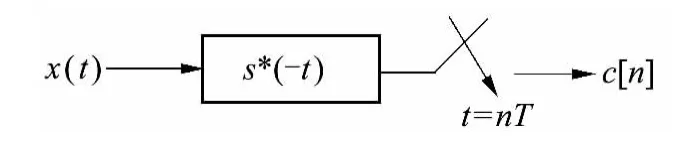
图1 单通道采样框架Fig.1 Framework of single channel sampling

由图1 可知，对于FRI 信号x(t)及采样周期T，实际采集到的向量为c= (c［1］，c［2］，…，c［N］)，其中

式中:n=1，2，…，N;S*(ω)为S(ω)的伴随矩阵的元素，S(ω)为s(t)的连续傅里叶变换，ω=2 k/ .实际上，只要选择

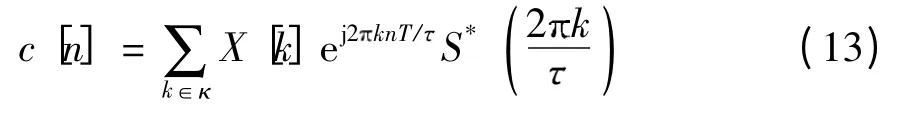
可见，对滤波后得到的采样向量c 进行离散傅里叶变换DFT{c}，再乘以S-1，就能得到傅里叶系数x.

在文献［5］的FRI 滤波器模型中，s*(- t)=Bsin(-cBt)，B=M/ ，2L ≤M ≤N，并且s(t)是一个带宽为B 的理想低通滤波器:

对于一个有限信号，采用FRI 滤波器的采样模型定义如下:

假设h(t)满足条件

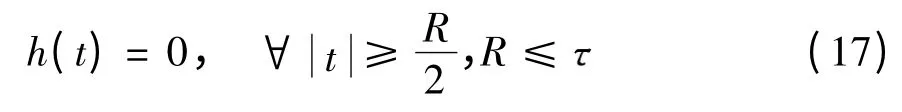
经过推算可以验证，当R ≤ 时，有以下公式成立:

其中，s3p(t)=s(t - )+ s(t)+ s(t + ).

2.2 SoS 滤波器

由于理想低通滤波器带宽是有限的，而脉冲信号在时域上是无限的，因此文献［5］的FRI 滤波器具有局限性，它不能扩展到无限脉冲信号.通常，工业超声回波信号的频率很高，但超声探头及转换硬件性能的限制使所获得的超声信号带宽远远低于实际的信号带宽，故存在较大的信息丢失.为此，基于FRI 滤波器组，在文献［6］的基础之上，文中提出了带宽不受限制的SoS 滤波器:

式中，bk≠0，bk=，

将它转化到时域上，有

同样，有限信号采用SoS 滤波器采样模型，定义为

选择正确的参数bk(kκ)，能够增强滤波器的抗噪性能，文中取长度为M 的汉明窗系数:

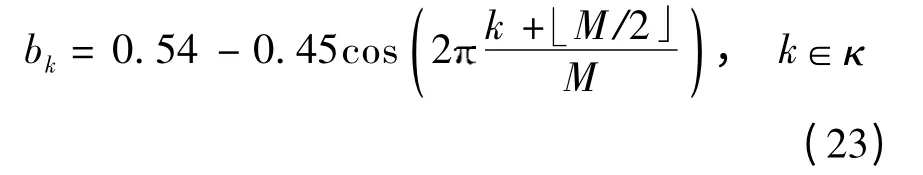
可知，bk=，因此滤波后的采样系数c［n］必定为实数.

3 实验及结果分析

3.1 Matlab 仿真结果分析

SoS 滤波法的实现步骤如下:

(1)输入包含L 个高斯脉冲的信号x(t)，高斯脉冲为

其中σ=7 ×10-3，周期= 1 s，时间延时和幅度是随机选择的;

(2)根据实际的超声检测，取脉冲个数L=5，κ={- L，- L +1，…，L -1，L}，M== 11 ;

(3)采用汉明窗系数满足式(23)(计算结果见图2)的g(t)对输入信号进行滤波;

图2 bk 的选取Fig.2 Selection of bk

根据式(7)-(9)对图3 所示信号进行滤波，SoS滤波器的实部如图4 所示，采样结果如图5 所示，原始信号的估计延时和幅度如图6 所示，所得到的重建信号如图7 所示，由图可见重建效果很好.

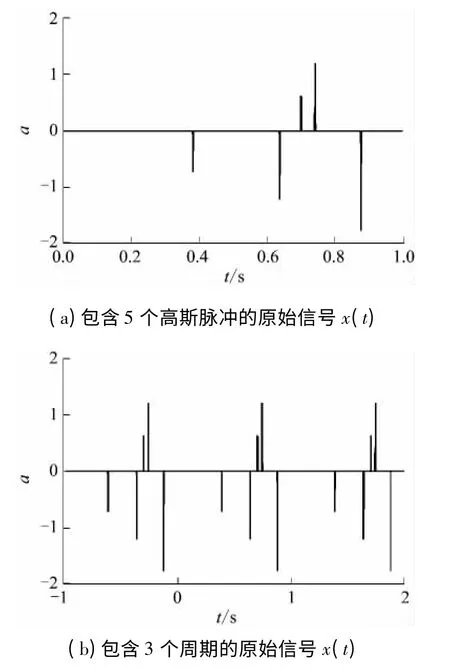
图3 包含不同周期的原始信号Fig.3 Original signals containing different periods

图4 SoS 滤波器的实部Fig.4 Real component of SoS filter

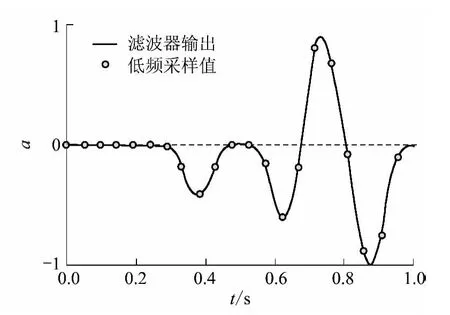
图5 滤波输出信号中采样的21 个值Fig.5 Twenty-one sampling values of filter output signal

图6 原始信号的估计延时和幅度Fig.6 Estimation time delay and amplitude of original signal

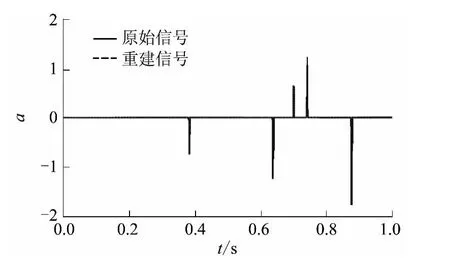
图7 仿真重建信号与原始信号对比Fig.7 Comparison of reconstruction signal with original signal in simulation

3.2 实测结果分析

(1)利用工业超声波成像系统采集一组一维原始信号(如图8 所示)，其中单一探头的中心频率fc=3.4235 MHz，系统的采样频率fs= 40 MHz，成像深度Rmax= 0.16 m，在被测物体中，超声波速c=1540 m/s，可以计算出信号的持续时间 '=2Rmax/c=2.08×10-4s;

(2)根据超声波工业探头的特性，将h(t)定为高斯脉冲是比较合适的，选择高斯参数σ=3 ×10-7s，因σ ≤ '，故可以使用滤波器(21)对采样数据进行滤波，结果见图9;

(3)取L=5，为了增强抗噪性能，设M=2 ×5 ×2+1=21，N=M=21，κ= {- 10，- 9，…，0，…，9，10}，采样周期T= '/N=2.08 ×10-4/21 s=9.91 μs;

(4)利用式(20)-(22)构造滤波器，计算采样向量c;

(5)利用式(14)计算傅里叶系数向量x;

(6)利用y=H-1x 求出向量y，从而得到方程组(9);

(7)利用零化滤波重建算法求解方程(9)，得到估计的延时和幅度如图10 所示，重建信号见图11.

图8 实测超声信号Fig.8 Actually measured ultrasonic signals

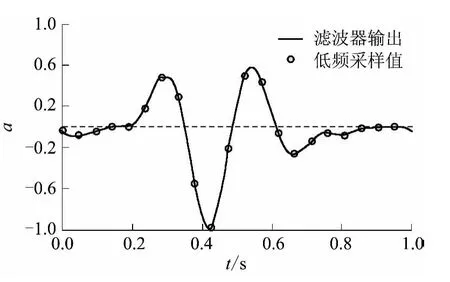
图9 滤波输出信号的采样值Fig.9 Sampling values of filter output signal

图10 原始超声信号的估计延时和幅度Fig.10 Estimation time delay and amplitude of original ultrasonic signal

图11 实测原始超声信号和重建信号比较Fig.11 Comparison of original ultrasonic signal with reconstruction signal in actual measurment

由重建效果可以看出，延时系数是精确的.在超声波成像系统中，延迟系数代表着缺陷的位置，因此，只要延时系数精确，就能准确地确定缺陷的位置.

4 结语

根据工业超声波信号频率较高的特点，基于FRI 滤波器组，文中提出了一种新的适用于工业超声信号处理的FRI 信号采集方法——SoS 滤波器法，Matlab 仿真和实测结果表明该方法是有效的，从而验证了CS 理论在工业超声波检测系统中应用的可行性.文中就CS 理论在工业超声波检测系统中的应用做了有益的探讨和实测数据仿真，进一步丰富了CS 理论.

［1］Donoho D L.Compressed sensing［J］.IEEE Transactions on Information Theory，2006，52(4):1289-1306.

［2］Candès E J，Romberg J，Tao T.Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information［J］.IEEE Transactions on Information Theory，2006，52(2):489-509.

［3］Candès E J.Compressive sampling［C］∥Proceedings of the International Congress of Mathematics.Madrid:European Mathematical Society，2006:1433-1452.

［4］Candès E J，Wakin M B.An introduction to compressive sampling［J］.IEEE Signal Processing Magazine，2008，25(2):21-30.

［5］Tur R，Eldar Y C，Friedman Z.Innovation rate sampling of pulse streams with application to ultrasound imaging［J］.IEEE Transactions on Signal Processing，2011，59(4):1827-1842.

［6］Wagner N，Eldar Y C，Feuer A，et al.Compressed beamforming in ultrasound imaging［J］.IEEE Transactions on Signal Processing，2012，60(9):4643-4657.

［7］Chernyakova T，Eldar Y C.Fourier domain beamforming:the path to compressed ultrasound imaging［J/OL］.Arxiv，2013:11(2013-07-24).http:∥arxiv.org/abs/1307.6345.

［8］Wagner N，Eldar Y C，Feuer A，et al.Compressed beamforming with applications to ultrasound imaging ［C］∥Proceedings of 2012 IEEE International Conference on Acoustics，Speech and Signal Processing.Kyoto:IEEE，2012:3641-3644.

［9］Friboulet D，Liebgott H，Prost R.Compressive sensing for raw RF signals reconstruction in ultrasound ［C］∥Proceedings of 2010 IEEE Ultrasonics Symposium.San Diego:IEEE，2010:367-370.

［10］Quinsac C，Basarab A，Kouamé D.Frequency domain compressive sampling for ultrasound imaging［J/OL］.Advances in Acoustics and Vibration，2012，2012:16(2012-04-05).http:∥dx.doi.org/10.1155/2012/231317.

［11］Quinsac C，Basarab A，Kouame D，et al.3D compressed sensing ultrasound imaging［C］∥Proceedings of 2010 IEEE Ultrasonics Symposium.San Diego:IEEE，2010:363-366.

［12］Quinsac C，Basarab A，Girault J，et al.Compressed sensing of ultrasound images:sampling of spatial and frequency domains ［C］∥Proceedings of 2010 IEEE Workshop on Signal Processing Systems.San Diego:IEEE，2010:231-236.

［13］Shi Guangming，Chen Chongyu，Lin Jie，et al.Narrowband ultrasonic detection with high range resolution:separating echoes via compressed sensing and singular value decomposition［J］.IEEE Transactions on Ultrasonics，Ferroelectrics and Frequency Control，2012，59(10):2237-2253.

［14］Vetterli M，Marziliano P，Blu T.Sampling signals with finite rate of innovation［J］.IEEE Transactions on Signal Processing，2002，50(6):1417-1428.

［15］Stoica P，Moses R.Introduction to spectral analysis［M］.Englewood Cliffs:Prentice-Hall，2000.

［16］Sarkar T K，Pereira O.Using the matrix pencil method to estimate the parameters of a sum of complex exponentials［J］.IEEE Antennas and Propagation Magazine，1995，37(1):48-55.