基于布尔矩阵和MapReduce的FP-Growth 算法*

陈兴蜀 张帅 童浩 崔晓靖

(四川大学 计算机学院，四川 成都 610065)

关联规则挖掘(ARM)是数据挖掘领域中一个非常重要且具有挑战性的研究课题.与其他数据挖掘算法相比，关联规则挖掘具有挖掘效率高、准确性好、理解性强等优点.通常，关联规则挖掘和频繁项集挖掘(FIM)密切相关，FIM 被认为是ARM 的先决条 件.ARM 常 用 的 算 法 有Apriori［1］、DHP［2-3］、DIC［4］、FP-Growth［5-6］等，在加速挖掘性能上，它们起着重要的作用.将这些算法应用于FIM，已取得了许多成果.

近年来兴起的云计算［7］以其超大规模、虚拟化、高可靠性、高扩展性等优点为海量数据的处理带来了新的解决方案.然而，目前针对云平台下的FIM的研究仍然很少.Gunopulos 等［8］已经证明:判断一个事务数据集中是否存在至少包括t 个项、支持度为min_sup 的频繁项集是非确定性多项式(NP)完全问题.面对海量数据，单机模式下频繁项集挖掘算法常常显得力不从心［9］，减少数据库扫描次数及并行扫描是提高效率的有效方法之一.因此，对FIM的并行计算和分布式计算已成为必然.Jiang 等［10］在Apriori 算法的基础上，应用向量元、子规则、父规则提高了关联规则的挖掘效率.Korczak 等［11］使用FP-Growth 算法挖掘客户交易行为，与Apriori 算法相比更具优势，但它们并没有实现真正意义上的并行计算.MapReduce［12］是一种简洁抽象的并行计算模型，Apache 基金会在此基础上实现了开源的并行平台Hadoop，该平台已在学术界和工业界得到了广泛 的 应 用.OPT-DIC［13］、MR-Apriori［14］、Apriori-like算法［15］与其他分布式Apriori 算法相比具有更好的性能和可伸缩性，但同步和通信等开销较大.为此，Yu 等［16］在Hadoop 平台上改进了Apriori 算法，尽管能处理一定的海量数据，但需要的时间并没有线性地减少，同时需要生成候选集才能产生最终的频繁集，并且该算法对事务数据的扫描次数也没有减少.PFP 算法［17］在FP-Growth 算法的基础上实现了并行化，按照项集划分数据，但需要扫描两次事务数据，在多个并行的节点上产生FP 树，不能实现数据的实时处理.

文中针对大规模海量数据，在Hadoop 并行平台上实现了基于布尔矩阵和MapReduce 的FP-Growth(BPFP)算法，并通过实验验证了该算法的有效性.

1 相关概念

1.1 布尔矩阵

记Ωn={1，2，…，n}.

定义1 设矩阵A=(aij)m×n，若满足aij{0，1}，(i，j)= Ωm×Ωn，则称A 为布尔矩阵.令为第k(k ≥1)个布尔矩阵，=(a(mk+1)j)1×n为一维矩阵且，记，若a(mk+1)j=，ε为最小支持度，则称为A 的第k 个扩展布尔矩阵(EBM)，^A 为扩展向量.记Ti(iΩmk+1)和Ij(jΩn)分别为EBM的第i 个行向量和第j 个列向量，为了表述方便，Ti和Ij在关联规则中分别代表事务名称和项集名称.

定义2 设Ii、Ij是扩展布尔矩阵A=(aij)m×n的列向量，构造转置元向量t= (1，1，…，1，0，则ωi=Ii·t 为Ii(关联规则中)在A 中出现的总次数;ωij= Ii·Ij- ami·amj，为(Ii，Ij)序列在A 中出现的总次数.

考虑到EBM 中元素的过滤，文中给出合取运算符∧的定义.

定义3 设aij、akj为扩展布尔矩阵A=(aij)m×n的元素，i，kΩm，定义

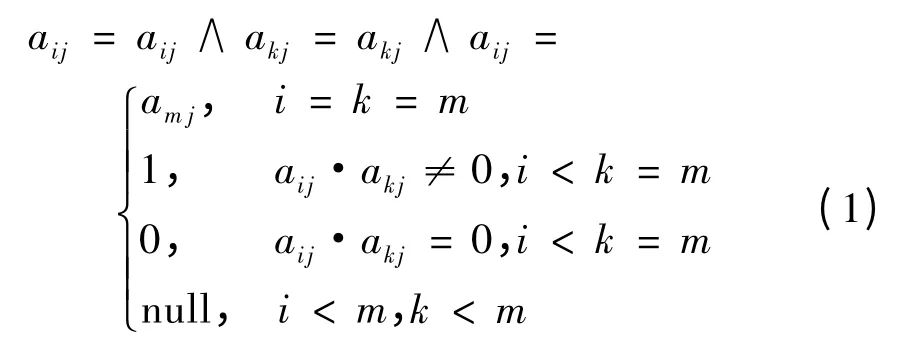
EBM 用于代替事务数据库，运算符∧用于过滤非频繁项集.

1.2 FP-Growth 算法

设I= {I1，I2，…，Im}是项目集合，T= {T1，T2，…，Tn}是一个(数据库)事务集合，事务Ti是项目的集合，Ti⊆I(iΩn).A(A ⊂I)的支持度sup(A)为T中包含A 的事务数.如果sup(A)≥ε，则A 是频繁项集.

FP-Growth 算法是一种FIM 算法，在挖掘频繁项集过程中需要扫描两次数据集:第1 次扫描是为了找出频繁1-项集的集合F1和支持度，并将F1按支持度递减的顺序插入表头项(记为L);第2 次扫描是利用频繁1-项集过滤数据库中的非频繁项，同时生成FP 树.将候选集压缩到FP 树上，可以大幅压缩候选集的规模.FP-Growth 算法发现所有频繁项集的过程如下:①构造频繁模式树FP 树;②在FP树上调用挖掘算法挖掘所有频繁项集.研究表明:对于挖掘长和短的频繁模式，FP-Growth 算法均是有效和可规模化的，并且其运算速度大约比Apriori 算法快一个数量级.因此，并行的FP-Growth 算法具有更快的运算效率，这是合乎逻辑的.

为了建立FP 树的路径、模式与布尔矩阵、EBM之间的联系，文中定义项的偏序关系“≺”，以建立项与序号1∶1 的关系.

定义4 对于任意项Ii，IjI，Ii≺Ij当且仅当Ii对应的序号小于Ij对应的序号.Ii的序号为Ii在EBM中对应的列序号.

定义5 设Lk={I1，I2，…，Ik-1}，IiT (iΩk-1)，HTID是由表头项的ID 组成的集合，如果LkHTID，则称Lk为项Ik的频繁模式集.

定义6 局部FP 树(LocalFPTree)是满足下列条件的一个树结构:

(1)它由一个根节点(值为null)、项前缀子树Tlocal和一个局部频繁项头表LHTable 组成.

(2)每个节点包括3 个域(item_name、count 和node_link)，item_name 由Ik及其频繁模式集组成，count 为支持度计数，node_link 是指向Tlocal中下一个具有相同项目节点的指针(无节点可链时为空).

(3)LHTable 的表项包括频繁项Ik的频繁模式集Lk、支持度计数(Tlocal中的总支持度计数)、节点链的头指针(指向模式树中具有Lk的第一个节点).

如果Ik是LocalFPTree 的叶子节点，则称Local FPTree 为TPTreek或者Ik的局部频繁树.图1 给出了项I3的LocalFPTree，它所生成的频繁项集是{{I3I2:4}，{I3I1:4}，{I3I2I1:2}}.

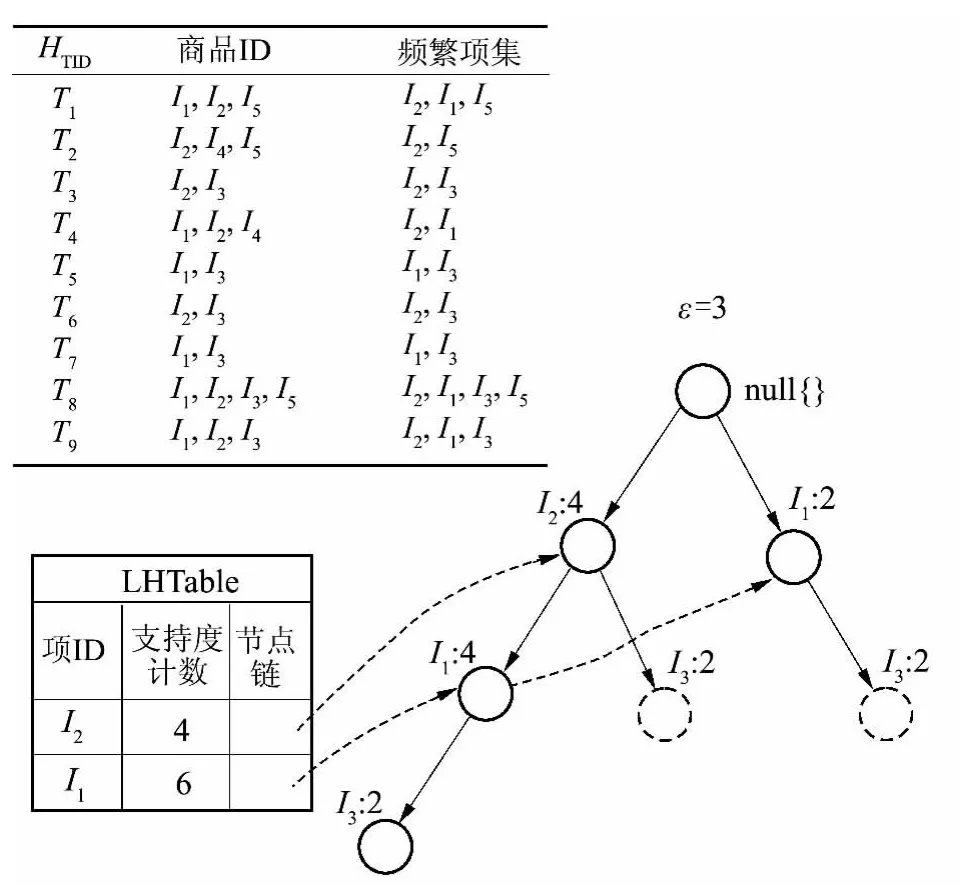
图1 项I3 的LocalFPTree Fig.1 LocalFPTree of item I3

TPTreek的构造算法描述如下:

{输入:Ik的条件模式基、F1和LHTable

输出:Ik的TPTreek

生成Ik的频繁模式集Lk;

∥根据定义4 排列项集

初始化LHTable，每项的支持度计数为0，node_link为null;

创建根节点，以“null{}”标记;

改进的FP-Growth 算法描述如下:

初始化canpat{pattern:0};

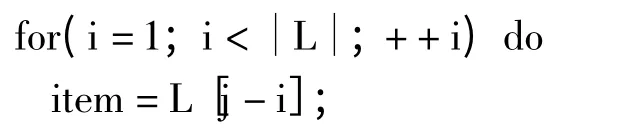
找出item 中所有的条件模式基构成

定理1 频繁模式的挖掘FP 树和各LocalFPTree 是等价的.

证明 设IkHTID，其局部频繁树为TPTreek，由定义6 可知，TPTreek中每个节点的item_name 是由Ik及其条件频繁模式集组成.因此，TPTreek产生的频繁模式等同于FP 树挖掘项Ik的频繁模式;由HTID中的元素对应的LocalFPTree 所挖掘的频繁模式组成的集合就是FP 树中挖掘频繁树的集合.故频繁模式的挖掘FP 树和各LocalFPTree 是等价的.证毕.

对于图1 中的事务集，未改进的FP-Growth 算法需要递归扫描FP 树9 次，而改进FP-Growth 算法只需要扫描FP 树6 次，降低了搜索FP 树的时间代价;另外，TPTreek为并行挖掘奠定了基础.

2 BPFP 算法

2.1 MapReduce 并行计算模型

Hadoop 是一个能够对大量数据分布式处理的软件架构，其核心组件是HDFS 和MapReduce.MapReduce是运行在大规模集群上的分布式数据处理模型，其处理过程主要分为两个阶段:Map 和Reduce.MapReduce 模型的定义如下［14］:

Map(k1，v1)→list(k2，v2)，

Reduce(k2，list(v2))→list(v2)，

2.2 BPFP 算法的实现及分析

BPFP 算法是针对PF-Growth 算法并基于EBM和MapReduce 而提出的.该算法采用MapReduce 并行计算模型进行并行计算，可以提高计算的效率;使用扩展布尔矩阵可以减少算法在计算过程中对事务数据的扫描次数.给定一个事务数据集T 和最小支持度ε，BPFP 算法使用两个MapReduce 来实现频繁项集的挖掘，具体流程见图2.

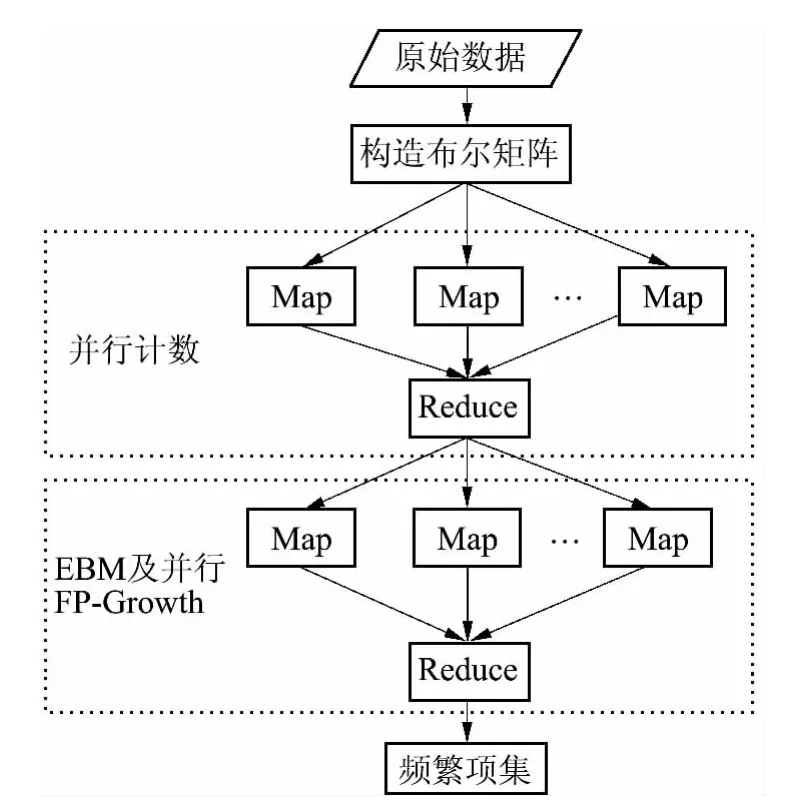
图2 BPFP 算法流程图Fig.2 Flowchart of BPFP algorithm

设有k 个节点，BPFP 算法步骤如下:

(1)构建布尔矩阵.将事务数据集T(m 个事务n 个项)转换为布尔矩阵A=(aij)m×n(BPFP 算法仅在此访问事务数据集，从而减少开销)，当相关的项存在时aij为1，否则为0.

(2)分片.将A 划分为k 块(A1，A2，…，Ak)，除了Ak外其他每个分块的数据大小相等.Hadoop 为每个分块构建一个Map 任务.

(3)并行计数.在每个Map 任务中，程序扫描对应的布尔矩阵Ai，利用MapReduce 并行计算每个项的支持度ε'.并行计数的空间和时间复杂度均为

(4)排序.对频繁1-项集按其支持度降序排序生成F_list.由于F_list 一般很小，因此通常将其放在内存中.此步骤一般可以在单机上进行操作，其空间复杂度为

(5)并行FP-Growth.在Map 阶段，对每一个Ai(iΩk)生成对应的EBM.同时对EBM 的每行进行频繁1-项集提取、排序操作，然后构造每个项的条件模式基;在Reduce 阶段，对于每个长度为1 的频繁项集，根据其条件模式基构建局部FP 树，并对该局部FP 树进行挖掘，最后生成频繁模式.

BPFP 算法中使用了EBM，当事务数据集更新后，它不需要对原有的事务数据进行扫描，只需要扫描更新后的数据集，再更新EBM，因此可以降低扫描空间，提高算法效率，同时也能实现数据的实时处理.并行计数的伪代码如下:

并行FP-Growth 算法的伪代码如下:

3 实验结果与分析

在BPFP 算法中采用EBM，可以减少系统的存储开销，提高数据访问的效率，特别是对于海量数据.假设I 由100 个项组成，T 有5 000 万个交易记录，即使每个项都是频繁的，在EBM 中每个元素占1 B，EBM 共占5000 MB，与原事务数据大小相比，存储空间占有率也变小了.如果对EBM 进行压缩，实际的存储空间占有率只有原来的十分之几甚至更少.当对EBM 进行分块时，得到的每个分块完全可以存入内存，这样保证了后续的挖掘不再扫描原始事务数据集，有效地提高了挖掘效率.

文中实验平台的基本配置见表1，1 个NameNode，5 个DataNodes，操作系统均为CentOS release 5.6(Final).每个DataNode 设置的mapper 的最大负载(mapred.tasktracker.map.tasks.maximum)为2，Reducer 的最大负载(mapred.tasktracker.reduce.tasks.maximum)也为2，Hadoop 的其他配置采用默认方式.文中采用的测试数据集为挖掘频繁项集领域常用的测试数据集［18］，如表2 所示.对数据集Connect、Accidents 和Webdocs 分别进行实验;对相同的数据集，选择不同的ε进行实验.

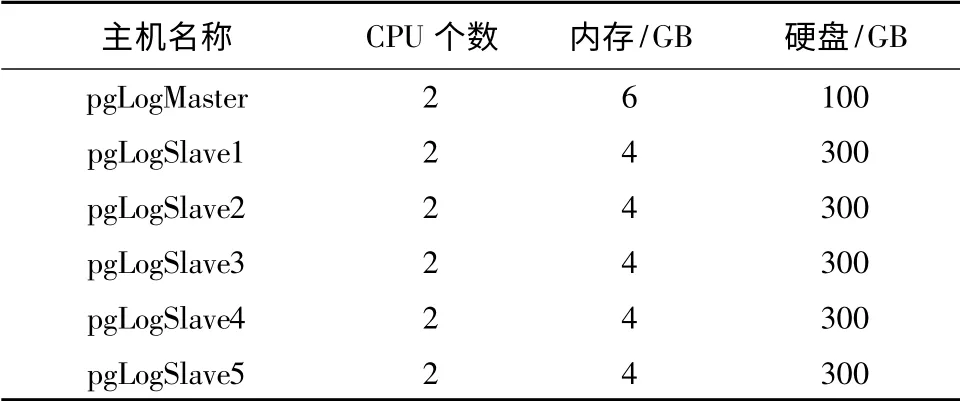
表1 实验配置Table 1 Configuration of experiment

使用数据集Webdocs2 和最小支持度为10%进行实验，P-Apriori 算法［12］(也使用了布尔矩阵)与BPFP 算法的性能(执行时间t 与节点数p 的关系)见图3.与P-Apriori 算法相比，BPFP 算法仅需要扫描一次布尔矩阵，并且不会因为快速增长的候选集而需要大量的时间和空间开销，因此BPFP 算法的时间开销优于P-Apriori 算法.

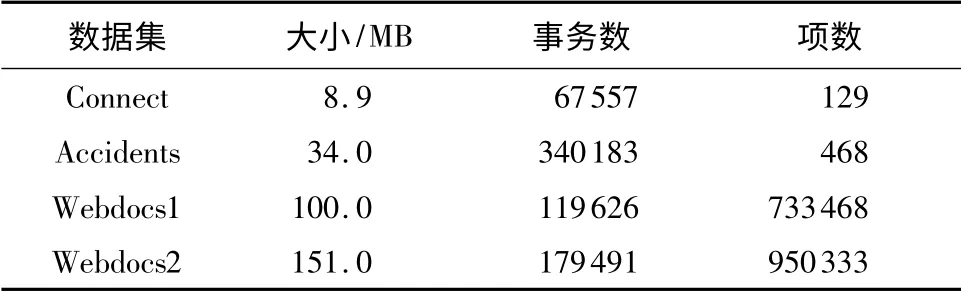
表2 测试数据集Table 2 Test datasets

图3 BPFP 与P-Apriori 算法的性能比较Fig.3 Comparison of performance between BPFP algorithm and P-Apriori algorithm

对于同一事务数据集，BPFP 算法的频繁项数Nf与支持度ε的关系如图4 所示，即符合Zipf 法则:支持度越小，频繁项数越大.因此，在并行FPGrowth 阶段需要的时间开销较大(见图5).文中通过加速比和加速率指标来评估BPFP 算法的性能.

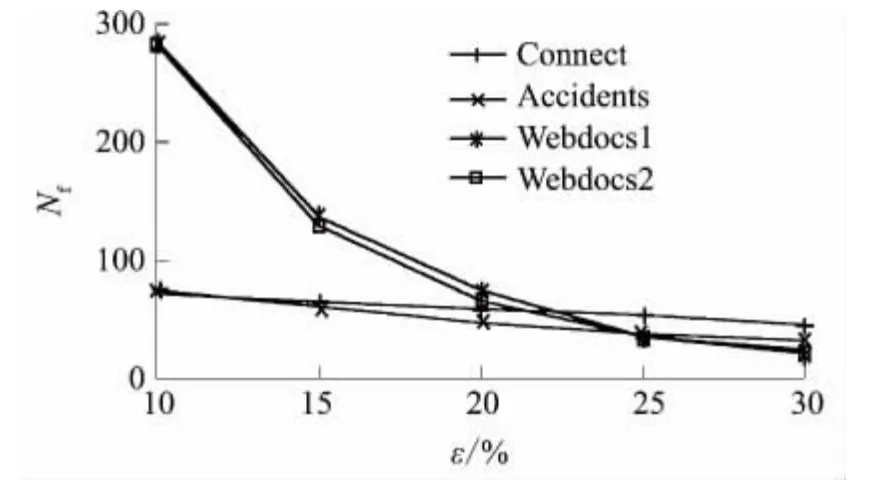
图4 支持度与频繁项集数的关系Fig.4 Support versus number of frequent item sets

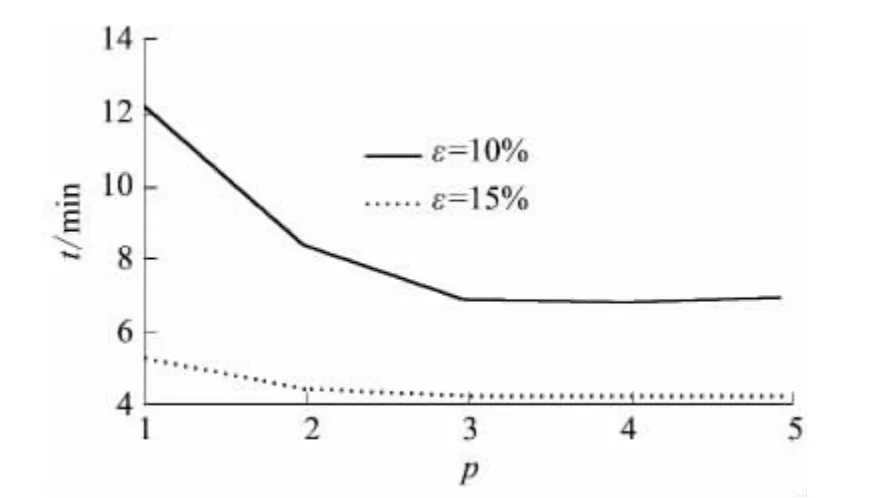
图5 同一数据集在不同支持度下的执行时间Fig.5 Execution time of the same dataset with different supports

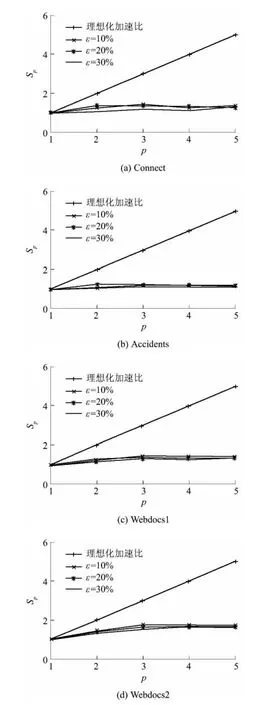
图6 BPFP 算法在不同实验条件下的加速比Fig.6 Speedup of BPFP algorithm under different experiment conditions

定义7 加速比Sp=t1/tp，其中t1是在单个节点上的执行时间，tp是在p(p ≥1)个节点上的执行时间.

定义8 加速率ks用于描述加速比的变化趋势.设(Dni，Si)表示Dni个节点所对应的加速比序列，其中，Dni{Ωn- Ωm}，n＞m，(m，n］为描述ks变化的自定义域，则

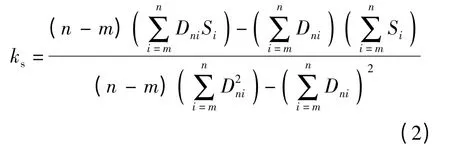
基于表1 的实验环境，使用表2 中的数据集，分别在5 个数据节点上和ε为10%、20%、30%的情况下进行实验，结果如图6 所示.从图可知:当数据集较小时，各个节点用于计算的时间较小，随着数据节点数的增加，用于节点通信的时间开销所占的比重越来越明显;对于数据较大的节点，计算时间较长，用于节点通信的开销所占的比重相对较小，因此图6(a)、6(b)中加速率ks的增长不太明显，趋于0(如图6(b)中ks在ε为10%、20%、30%时分别为0.0508、0.025 8、0.023 2)，而图6(c)、6(d)中在数据节点数小于3 时，ks较大(如图6(d)中ks在ε为10%、20%、30%时分别为0.3700、0.3200、0.2550)，随着数据节点数的增加，ks趋于0.因此，在规模较小的数据集中，BPFP 算法的数据交换成本太大，很快就达到阿姆达尔定律的限制;对于规模较大的数据集，数据交换成本所占比重降低，加速比表现更优，故BPFP 算法在规模较大的数据集上的性能更优.

使用数据集Webdocs2 和最小支持度为10%进行实验，BPFP 与PFP 算法［9］的执行时间如图7 所示.从图中可知，当数据节点数较小时，BPFP 算法需要在EBM 和事务数据间相互映射，因此所需要的时间开销较PFP 算法大;随着数据节点数的增加，BPFP算法使用EBM 对事务数据进行压缩，从而减少了节点间的通信开销，因此所需要的时间开销较PFP 算法小.

图7 BPFP 与PFP 算法的执行时间比较Fig.7 Comparison of execution time between BPFP algorithm and PFP algorithm

4 结论

文中基于布尔矩阵和MapReduce 提出了改进的FP-Growth 算法(BPFP 算法).该算法将事务数据集转化为布尔矩阵存储，不仅减少了算法对事务数据集的扫描次数，而且降低了数据的存储空间.非递归地构建FP 树和扫描FP 树会产生频繁项集，可减少条件模式基和FP 树的规模，从而降低算法的时间和空间开销.MapReduce 为BPFP 算法提供了并行化框架，在很大程度上提高了算法的挖掘效率，使算法具有很好的拓展性、容错性.实验结果表明，BPFP算法是有效、可行的，能较大地提高执行效率，具有较好的加速比及加速率.

对于规模较小的数据集，由于节点的通信开销所占比重较大，故BPFP 算法与单机(单节点)模式算法相比没有太大的优势.今后将针对小文件小数据的关联挖掘的并行化进行研究，改进BPFP 算法在处理小文件小数据时的不足，使之同样适用于高效的并行化数据挖掘.

［1］Agrawal R，Srikant R.Fast algorithms for mining association rules ［C］∥Proceedings of the 20th VLDB Conference.San Francisco:Morgan Kaufmann Publishers Inc，1994:487-499.

［2］Park J，Chen M，Yu P.Using a hash-based method with transaction trimming for mining association rules ［J］.IEEE Transactions on Knowledge and Data Engineering，1997，9(5):813-825.

［3］Zel S A，Guvenir H A.An algorithm for mining association rules using perfect hashing and database pruning［C］∥Proceedings of the 10th Turkish Symposium on Artificial Intelligence and Neural Networks.Berlin:Springer-Verlag，2001:257-264.

［4］Brin S，Motwani R，Ullman J D，et al.Dynamic itemset counting and implication rules for market basket data［C］∥Proceedings of the 1997 ACM SIGMOD International Conference on Management of Data.New York:ACM，1997:255-264.

［5］Han Jiawei，Pei Jian，Yin Yiwen.Mining frequent patterns without candidate generation ［C］∥Proceedings of the2000 ACM SIGMOD International Conference on Management of Data.Dallas:ACM，2000:1-12.

［6］Han Jiawei，Pei Jian，Yin Yiwen，et al.Ming frequent patterns without candidate generation:a frequent-pattern tree approach［J］.Data Mining and Knowledge Discovery，2004，8(1):53-87.

［7］Aaron Weiss.Computing in the clouds ［J］.netWorker，2007，11(4):16-25.

［8］Gunopulos D，Khardon R，Mannila H，et al.Discovering all most specific sentences［J］.ACM Transactions on Database Systems，2003，28(2):140-174.

［9］Yu Kun-Ming，Zhou Jiayi，Hong Tzung-Pei，et al.A loadbalanced distributed parallel mining algorithm［J］.Expert Systems with Applications，2010，37(3):2459-2464.

［10］Jiang Y，Wang J.An improved association rules algorithm based on frequent item sets［J］∥Procedia Engineering，2011，15:3335-3340.

［11］Korczak Jerzy，Skrzypczak Piotr.FP-growth in discovery of customer patterns［M］∥Data-Driven Process Discovery and Analysis:First International Symposium.Heidelberg:Springer-Verlag，2012:120-133.

［12］Dean Jeffrey，Ghemawat Sanjay.MapReduce:simplified data processing on large clusters［J］.Communications of the ACM，2008，51(1):107-113.

［13］Paranjape P，Deshpande U.OPT-DIC:an efficient algorithm for distributed association rule mining［C］∥Proceedings of the 2009 International Conference on Computer Engineering and Applications.Singapore:IACSIT Press，2011:450-455.

［14］Wu Gang，Zhang Huxing，Qiu Meikang，et al.A decentralized approach for mining event correlations in distributed system monitoring［J］.Journal of Parallel and Distributed Computing，2013，73(3):330-340.

［15］Aouad L M，Le-Khac N A，Kechadi T M.Performance study of distributed Apriori-like frequent itemsets mining［J］.Knowledge and Information Systems，2010，23(1):55-72.

［16］Yu Honglie，Wen Jun，Wang Hongmei，et al.An improved Apriori algorithm based on the boolean matrix and hadoop［J］.Procedia Engineering，2011，15:1827-1831.

［17］Li Haoyuan，Yi Wang，Zhang Ming，et al.PFP:parallel FP-growth for query recommendation［C］∥Proceedings of the 2008 ACM Conference on Recommender Systems.New York:ACM，2008:107-114.

［18］Frequent Itemset Mining Implementations Repository.Frequent itemset mining dataset repository:FIMI dataset［EB/OL］.［2013-04-20］.http:∥fimi.cs.helsinki.