斜桩定位算法的研究及应用

2014-08-16马保卫

测绘通报 2014年3期

马保卫

(测绘出版社，北京100045)

一、引言

无论是在码头还是桥梁工程中，桩基都是一个重要的组成部分，其定位的精度将直接影响工程的质量。为使定位工作顺利进行，需要测量人员利用仪器指挥作业船只移动到设计沉桩位置。目前，近岸时比较常规的做法有：① 全站仪坐标法，即在打桩船上安装固定棱镜，建立3～4个固定点，经坐标转换后，通过控制这些固定点达到间接完成桩基定位的目的[1]；② 前方交会法，即利用桩心设计坐标与岸上控制点的位置关系，求出左右切点的观测角，并通过3台全站仪实时控制打桩船的移动，以完成桩基定位。离岸较远时可以利用基于GPS RTK技术的打桩定位系统，直接控制打桩船移动到桩的设计位置。但该系统也有许多不足之处，对贯入度、桩顶标高等的控制还有待完善。

利用常规方法进行桩基定位时，直桩的计算方法比较简单，且计算精度高，完全能够满足工程需要。但对于斜桩，由于定位数据采用的是近似算法，精度受到一定的影响，对工程质量有一定的影响，因此有必要对斜桩定位数据的计算方法作进一步的研究，以提高放样的精度，从而保证工程的施工质量。

二、直桩、仰俯桩定位原理

如图1所示，测站坐标、桩心设计坐标和桩的半径已知，以此可以计算出测站到桩心的方位角，并可以计算出小夹角(即测站和桩心的连线与切线之间的夹角)，此时可以得到测站和桩之间的左、右切方位角。在放样时，同时在3个测点上架设经纬仪或全站仪，将水平角度调到待放桩的左或右切方位角上，然后指挥作业船只移动。其中，两台仪器起控制作用，一台仪器起校核作用，以防止出现定位错误。

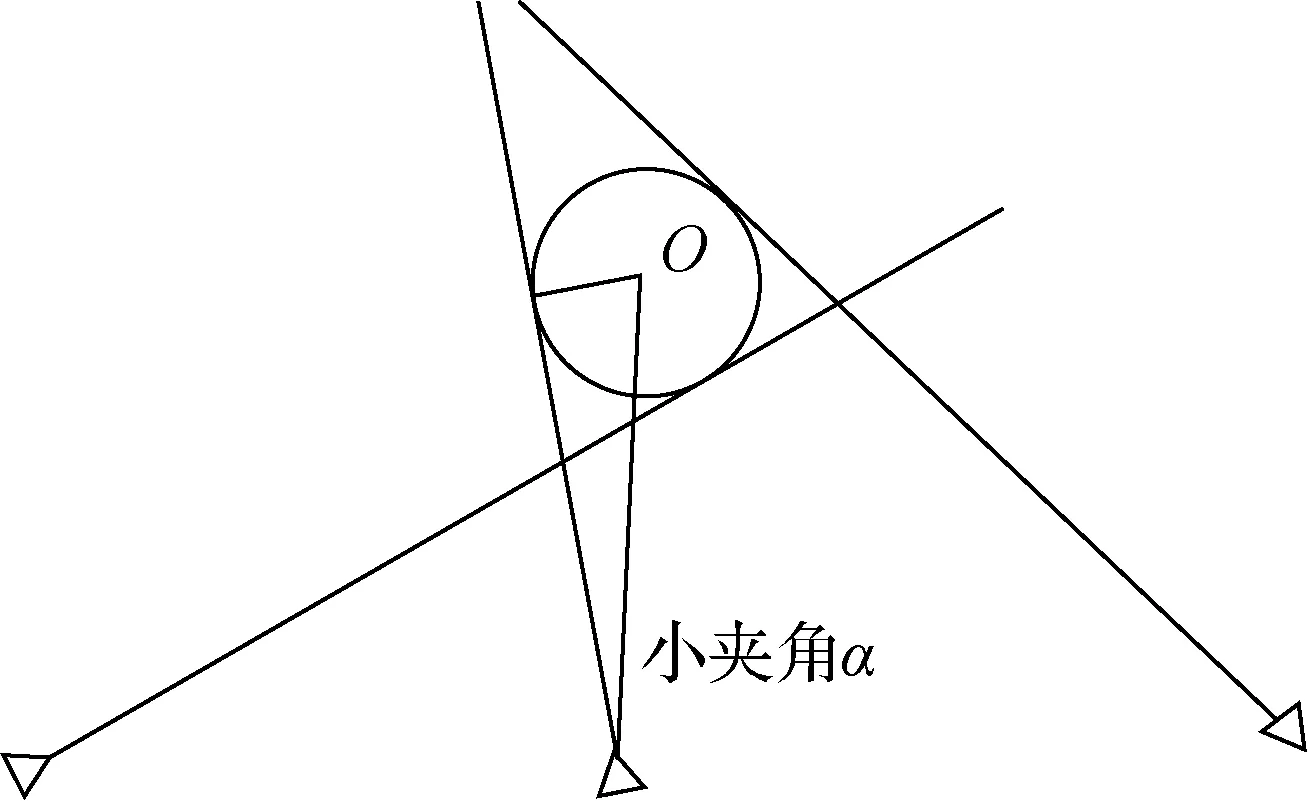
图1 利用前方交会对管桩定位的原理

桩的定位精度主要受交会角度、距离等因素的影响[2]。由于直桩的中心线平面位置不变，因此竖直角的改变不会影响平面定位的结果。通常是将两台仪器的竖直角固定在设计标高或控制标高的位置，以控制桩的标高；另外一台仪器随时检查桩的垂直度情况。

对于斜桩的定位，传统的方法是在控制平面处按照直桩进行放样数据的计算，该方法忽略了桩倾斜和船尾扭动后控制截面变成椭圆的现实[3]，从而给放样数据带来计算误差。

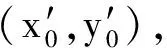
对于仰桩

(1)

对于俯桩

(2)

求出新的桩心坐标后，按照直桩的计算方法(即将控制截面近似为圆形)计算左、右切方位角。

三、仰俯桩定位精密算法

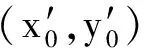
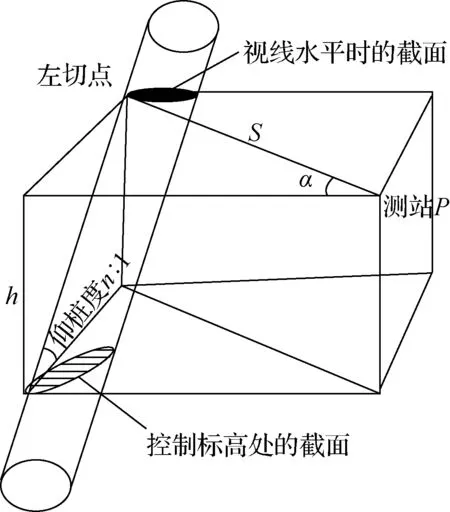
图2 斜桩改进算法示意图

(3)

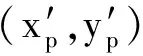
(4)

在该坐标系下建立切线方程和椭圆方程组

(5)

式中，短半轴b为桩的半径r；长半轴a=r/sin(arctann)。

测站P到左切点的方位角α=arctan((y1-yp)/(x1-xp)), 视线从水平移动到控制标高处变动的角度α0=arcsin(h/nS)。其中，h为提高量；n为仰俯比例；S为测站和水平左切点之间的距离。

此时，控制标高位置的左切方位角α′=α±α0，俯桩时为“+”，仰桩时为“-”。

四、应用实例

在某工程中，对斜桩利用传统的近似算法和本文改进后的算法分别进行计算，计算结果见表1。

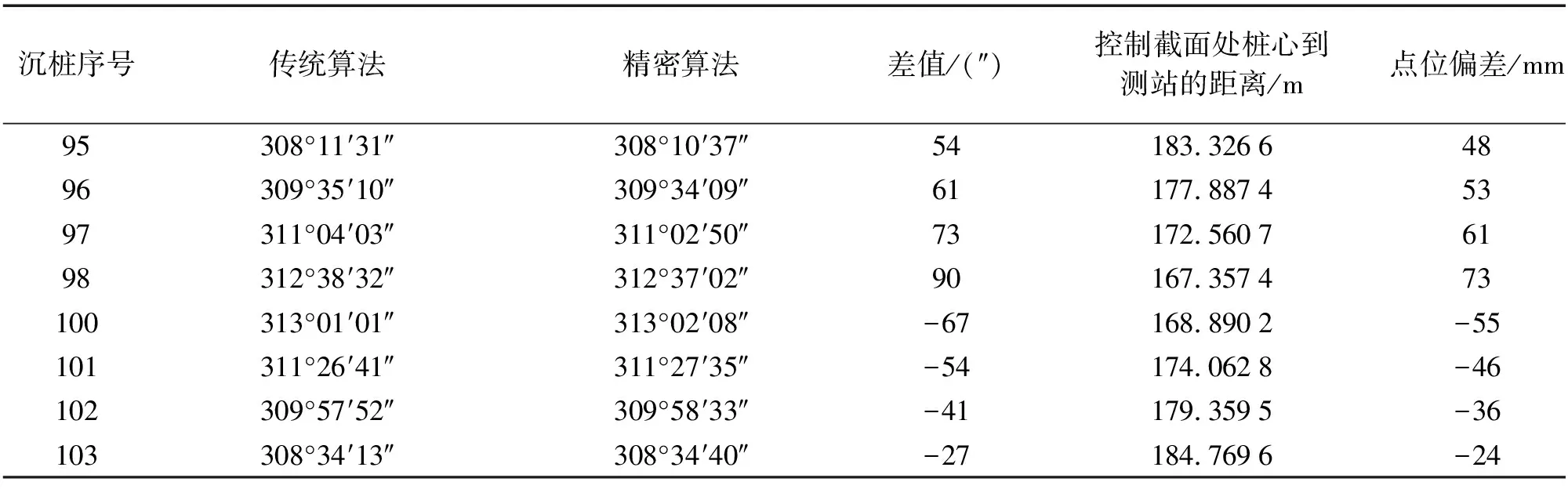
表1 两种方法计算结果对照表

从表1可知，传统算法与精密算法在放样角度上存在较大的差异，由此引起的桩位偏差也较大(最大已达到73 mm)，而桩基工程规范规定，桩位误差一般不应大于100 mm。考虑到放样过程中其他因素的影响，最后的桩位误差很有可能超出规范的规定，更有可能因为误差过大需要报废已经完成的桩基，从而造成人力、物力的浪费。而精密算法则能有效地提高计算精度，从根本上保证了桩基定位的质量。