L-R-Smash Products for Hopf Quasigroups

LI Shihong, LI Guanghu

(College of Science,Nanjing Agricultural University,Nanjing 210095,Jiangsu)

1 Introduction and preliminaries

It is well-known that the only parallelizable spheres areS1,S3,S7.The first two are groups andS7is something weaker(a Moufang loop or Moufang Quasigroup).Recently Klim and Majid in[1]introduced the concept of Hopf quasigroup and Hopf coquasigroup in order to capture the quasigroup features of the(algebraic)7-sphere.These are generalizations of Hopf algebras that are not required to be(co)associative.The lack of(co)associativity is compensated by conditions involving the antipode.

In this paper,we first introduce the concept of LR-smash products for Hopf quasigroups.Then we give a necessary and sufficient condition making L-R-smash product into Hopf quasigroups.

We work over a fixed fieldk.Unadorned tensor product symbol represents the tensor product ofk-vector spaces(see[2-11]).In what follows,we recall some definitions for Hopf quasigroups and Hopf coquasigroups used in this paper from[1,12-19].

Definition 1.1A Hopf quasigroup is a possibly-nonassociative but unital algebraHwith productμ:HH➝Hand unit 1:k➝Hequipped with algebra homomorphismsΔ:H➝HH,ε:H➝kforming a coassociative coalgebra and a linear mapS:H➝Hsuch that

Definition 1.2A Hopf coquasigroup is a unital associative algebraAwith counital algebra homomorphismsΔ:A➝AA,ε:A➝kand a linear mapS:A➝Asuch that

We use Sweedler notation for coproduct:for allh∈H,Δ(h)=h1h2(summation implicit).Thus,in terms of the Sweedler notation,the Hopf quasigroup condition(1)and(2)can be expressed by

for allg,h,h1,h2∈H.Dually,the Hopf coquasigroup conditions(3)and(4)come out as

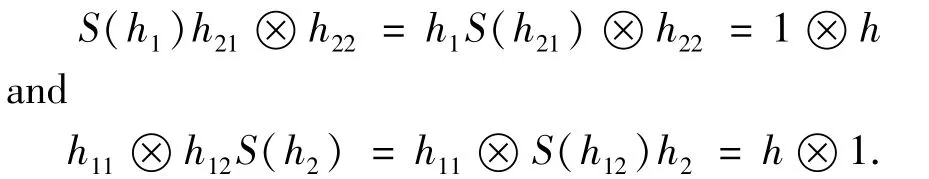
In this paper,the above mapSin Definition 1.1 or Definition 1.2 is called an antipode.A Hopf quasigroupHis flexible if for allg,h,h1,h2∈H,h1(gh2)=(h1g)h2;and alternative if also for allg,h,h1,h2∈H,h1(h2g)=(h1h2)g,h(g1g2)=(hg1)g2;and Moufang if for allf,g,h∈H,h1(g(h2f))=((h1g)h2)f.

Definition 1.3LetHbe a Hopf quasigroup.A vector spaceVis called a leftH-quasimodule if there is a linear mapα:HV➝Vwritten asα(hv)=h⇀vsuch that

for allh∈H,v∈V.

Similarly,we can define a rightH-quasimodule,that is,there is a linear mapβ:VH➝Vwritten asβ(vh)=v↼hsuch that

for allh∈H,v∈V.If a vector spaceVis both a leftH-quasimodule and rightH-quasimodule,and for allh,g∈H,v∈V,the following condition

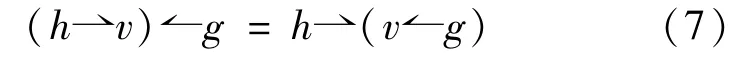
holds,then we call it anH-biquasimodule.

Definition 1.4An algebraA(not necessarily associative)is a leftH-quasimodule algebra ifAis a leftH-quasimodule and the following conditions hold:

for allh∈H,a,b∈A.

Similarly,we give the concept of a rightH-quasimodule algebra,that is,Ais a rightH-quasimodule and the following conditions hold:

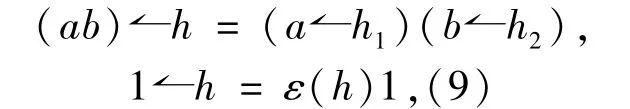
for allh∈H,a,b∈A.

LetHbe a Hopf quasigroup with antipodeS,andAan(not necessarily associative)algebra.ThenAis called anH-biquasimodule algebra if the following conditions hold:

1)Ais anH-biquasimodule with the leftH-quasimodule structure map“⇀”and the rightH-quasimodule structure map“↼”;

2)Ais not only a leftH-quasimodule algebra with the leftH-quasimodule action“⇀”but also a rightH-quasimodule algebra with the rightH-quasimodule action“↼”.

Definition 1.5A coalgebraCis a leftH-quasimodule coalgebra ifCis a leftH-quasimodule and

for allh∈H,c∈C.

Similarly,we give the concept of a rightH-quasimodule coalgebra,that is,Cis a coalgebra and a rightH-quasimodule and the following conditions hold:

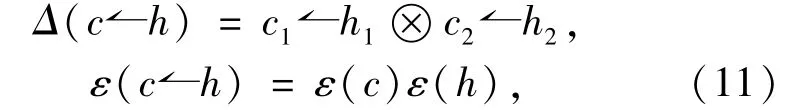
for allh∈H,c∈C.

LetHbe a Hopf quasigroup with antipodeS,andCa coalgebra.ThenCis called anH-biquasimodule coalgebra if the following conditions hold:

1)Cis anH-biquasimodule with the leftH-quasimodule structure map“⇀”and the rightH-quasimodule structure map“↼”;

2)Cis not only a leftH-quasimodule coalgebra via the action“⇀”but also a rightH-quasimodule coalgebra via the action“↼”.

AnH-biquasimodule Hopf quasigroup is a Hopf quasigroup which is anH-biquasimodule algebra and anH-biquasimodule coalgebra.In a similar way,we can give the conception ofH-biquasimodule Hopf coquasigroups.

2 L-R-Smash products for Hopf quasigroups

In this section,we introduce L-R-smash products for Hopf quasigroups,and give a necessary and sufficient condition making the L-R-smash product into Hopf quasigroups,which generalizes some important results in several references.

Lemma 2.1For any Hopf quasigroupH,Δ,εare the coproduct and counit ofHrespectively,andS:H➝His a linear map satisfying(1)and(2).Then

1)εS=ε;

2)m(Sid)Δ=ε(h)1=m(idS)Δ;

3)Sis antimultiplicative:S(hg)=S(g)S(h)for allh,g∈H;

4)Sis anticomultiplicative:Δ(S(h))=S(h2)S(h1)for allh∈H.

ProofSimilar to the standard Hopf algebras,we can easily prove 1).From[1],we can got the proof of 2)～4).

In what follows,we always assume thatHis a Hopf quasigroup,andAanH-biquasimodule Hopf quasigroup,such that the following conditions hold:for allg,h∈Handa∈A,

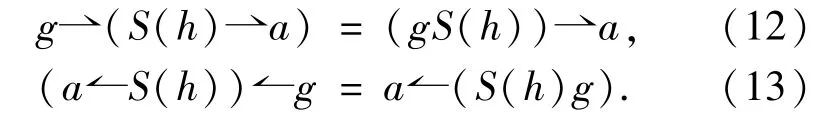
Theorem 2.2LetHbe a Hopf quasigroup,andAan alternativeH-biquasimodule Hopf quasigroup.Then the L-R-smash productA#Hbuilt onAHwith tensor coproduct and unit and for allg,h∈H,a,b∈A,

is a Hopf quasigroup if and only if the following conditions hold:

ProofSuppose(16)and(17)hold.To see thatΔis an algebra homomorphism,for alla,b∈A,h,l∈H,we compute

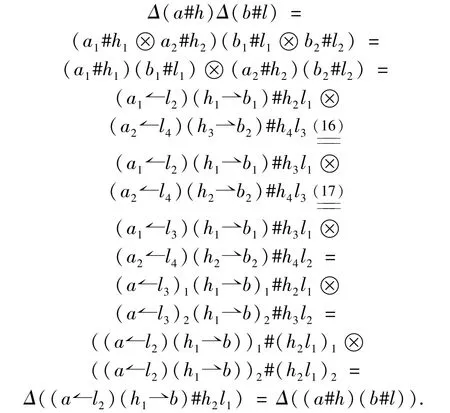
It is easy to prove that the counitεA#HofA#His an algebra homomorphism.It remains to check the Hopf quasigroup identities(1)and(2)hold.For alla,b∈A,h,l∈H,we compute

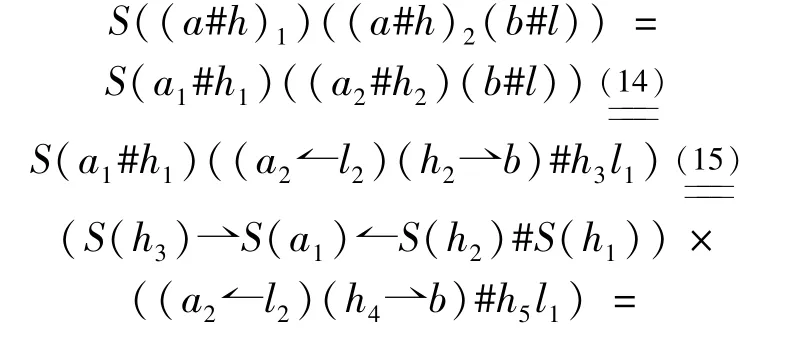
In the above equalities(∗),(∗∗)and(∗∗∗)come from the conditions(16)and(17).Next,in a similar way,we have

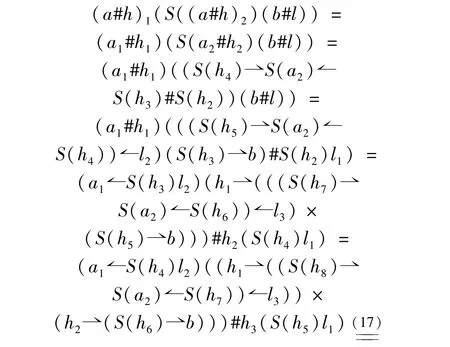
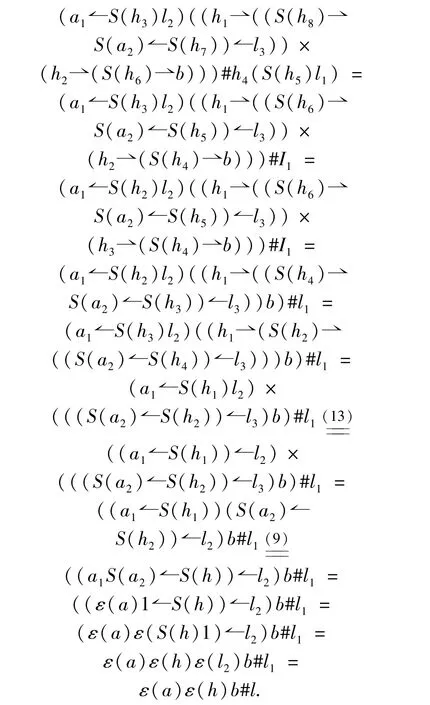
So,the relation(1)for the L-R-smash productA#Hholds.In a similar way,we can show the equality(2).

Conversely,ifA#His a Hopf quasigroup,then from the fact thatΔis an algebra homomorphism,we have

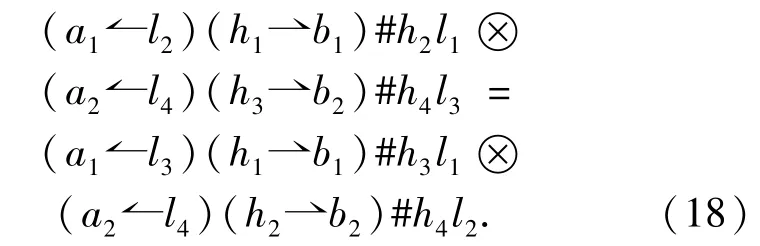
In the above equality(18),if takingh=1Handb=1A,then

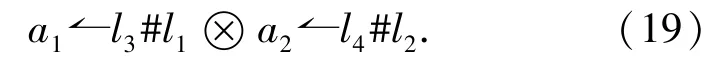
By applyingidAεHεAidHto both sides of(19),we have(17).

In the above equality(18),if takingl=1Handa=1A,then

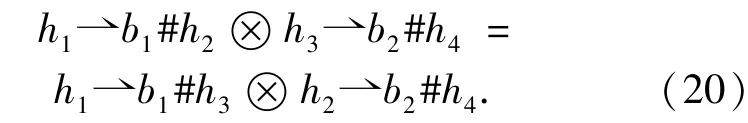
By applyingεAidHidAεHto both sides of(20),we obtain(16).This completes the proof.

In the above theorem,if the right quasiaction is trivial,then(17)holds.Hence we have the following corollary which is the main theorem in[13].

Corollary 2.3LetHbe a Hopf quasigroup,Aa leftH-quasimodule Hopf quasigroup.Then a smash productA#Hbuilt onAHwith tensor coproduct,counit and unit,whose multiplication and antipode are given by

is a Hopf quasigroup if and only if the conditions(12)and(16)hold.

In particular,ifHis cocommutative and the quasimodule ofAis exactly a module,then(12)and(16)hold.So,A#His a Hopf quasigroup in[1].

IfAandHin Theorem 2.2 are associative,they are usual Hopf algebras.Then we get the main result in[2].

Corollary 2.4Let(A,⇀,↼)be anH-bimodule bialgebra andA#Hthe L-R-smash product.ThenA#His a bialgebra if and only if(16)and(17)hold.

In this case,ifAandHare Hopf algebras,thenA#His a Hopf algebra.

Remark 2.5By the above duality,we can also give a necessary and sufficient condition making the LR-smash coproduct into a Hopf coquasigroup.

[1]Klim J,Majid S.Hopf quasigroups and the algebraic 7-sphere[J].J Algebra,2010,323(11):3067-3110.

[2]Zhang L Y.L-R smash products for bimodule algebras[J].Prog Nat Sci,2006,16(6):580-587.

[3]Sweedler M E.Hopf Algebras[M].New York:Benjamin,1969.

[4]蔡芝敏,张良云.Hopf模余代数结构定理[J].四川师范大学学报:自然科学版,2007,30(4):485-487.

[5]黄辉,牛瑞芳,张良云.弱Hopf代数与(s,i)双代数的自由积[J].四川师范大学学报:自然科学版,2010,33(4):443-446.

[6]李菲菲,陈园园,张良云.关于余模余代数的L-R-smash余积和L-R扭曲余积[J].浙江大学学报:理学版,2012,39(2):123-129.

[7]张鹏,张良云,牛瑞芳.扭Smash积的整体维数[J].浙江大学学报:理学版,2011,38(1):1-3.

[8]张良云.Lie余模和Lie双代数的构造[J].中国科学,2008,38(3):249-259.

[9]魏波,张良云.弱Hopf代数上的R-Smash积[J].数学半年刊,2008,25(1):67-75.

[10]杨冲,王勇,张良云.由Lazy 2-余循环诱导的扭曲Hopf模的基本结构定理[J].数学半年刊,2009,6(2):225-231.

[11]李彦超,王勇,张良云.弱Hopf代数上的β-特征代数[J].南京师范大学学报:自然科学版,2009,32(4):36-41.

[12]López M P,Nóvoa E V.The antipode and the(co)invariants of a finite Hopf(co)quasigroup[J].Appl Categor Stru,2013,21(3):237-247.

[13]Brzeziński T,Jiao Z M.Actions of Hopf quasigroups[J].Commun Algebra,2012,4(2):681-696.

[14]Brzeziński T,Jiao Z M.R-smash products of Hopf quasigroups[J].Arab J Math,2012,1(1):39-46.

[15]Jiao Z M,Wang Y L.The smash coproduct for Hopf quasigroups[J].Inter Elect J Algebra,2012,12:94-102.

[16]焦争鸣,赵晓凡.几乎余交换和拟三角Hopf余拟群[J].河南师范大学学报:自然科学版,2012,40(5):1-2.

[17]Brzeziński T.Hopf modules and the fundamental theorem for Hopf(co)quasigroups[J].Inter Elect J Algebra,2010,8:114-128.

[18]Klim J,Majid S.Bicrossproduct Hopf quasigroups[J].Commun Math Univ Carolinae,2011,51(2):287-304.

[19]Fang S H,Wang S H.Twisted smash product for Hopf quasigroups[J].J Southeast University:Eng Ed,2011,27(3):343-346.