易混易错的条件概率问题

● (黄陂一中盘龙校区 湖北武汉 430312)

条件概率是《新课程标准》实施后新增加的内容，它较以往互斥事件和独立事件的概率求法有很大区别，且与独立事件容易混淆.很多学生因此辨别不清，特别是条件概率中的条件变复杂时，学生更是无所适从，理不清头绪，自然成了难点.条件概率已成为近几年高考的新热点，而且难度不断加深，题目也由选择、填空题逐步变化在解答题中呈现，应该引起足够的重视！据高考结果统计，学生在条件概率问题上的得分情况并不乐观,笔者就如何辨析及求解条件概率问题整理如下，以帮助学生走出迷雾.

1 定义回顾

设A和B为2个事件，P(A)>0，那么，在A“已发生”的条件下，B发生的条件概率P(B|A)读作A发生的条件下B发生的概率．定义为

思考13张奖券中只有1张能中奖,现分别由3名同学无放回地抽取,问最后1名同学抽到中奖奖券的概率是多少？

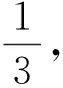
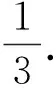
思考23张奖券中只有1张能中奖,如果在第1名同学没有抽到中奖奖券的条件下，最后1名同学抽到中奖奖券的概率是多少？

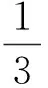
正解用Ω表示3名同学可能抽取的结果全体，Ω={YNN,NYN,NNY}．既然已知事件A必然发生，那么只需在A={NYN,NNY}的范围内考虑问题，在事件A发生的情况下事件B发生，等价于事件A和事件B同时发生，即AB发生．而事件AB中仅含一个基本事件NNY，因此

问题的关键是条件概率发生的样本空间发生了变化，由Ω={YNN,NYN,NNY}，得A={NYN,NNY}.

2 典例剖析

例1某市准备从7名报名者(其中男4人，女3人)中选3个人参加3个副局长职务的竞选.若选派的3个副局长依次到A，B，C局上任，求

(1)所选3个人中A局为男副局长的概率；

(2)所选3个人中A局为男副局长，B局为女副局长的概率；

(3)A局是男副局长的情况下，B局为女副局长的概率.

分析此题的关键在于读懂题意，能够辨别独立事件与条件概率.第(2)和第(3)小题容易混淆，第(2)小题中“A局为男副局长，B局为女副局长”是相互独立事件同时发生，第(3)小题中“A局是男副局长的情况下B局为女副局长”考查条件概率，正确运用公式求解即可.

(2)记D=A局是男副局长，E=B局为女副局长，事件D与E相互独立，则

(3)方法1记D=A局是男副局长，E=B局为女副局长,则

方法2记D=A局是男副局长，E=B局为女副局长,则

方法3(缩小样本空间)既然A局是男副局长，只需考虑B局和C局，B局只能从3个女副局长中选1个，C局任意选，则

评注独立事件同时发生概率公式P(AB)=P(A)P(B),条件概率求解的一般方法为：

(3)缩小样本空间.

例2在一个盒子中有大小一样的20个球,其中10个红球,10个白球,每个人从盒子中摸出1个球，摸后不放回，然后下一个人接着摸球.

(1)求第1个人摸出1个红球的概率；

(2)求第1个人摸出1个红球,紧接着第2个人摸出1个白球的概率；

(3)求在第1个人摸出1个红球的条件下,第2个人摸出1个白球的概率.

解记“第1个人摸出红球”为事件A，“第2个人摸出白球”为事件B，则

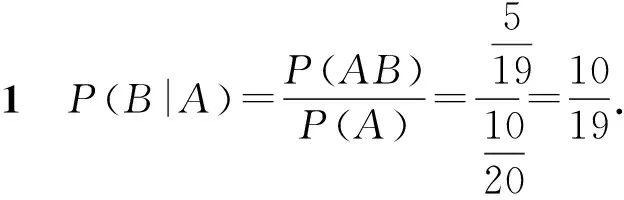
方法3(缩小样本空间)第1次摸出的球不再考虑，第2次只能从剩余的19个球中去摸，摸到白球的可能有10种，则

评注以上2道概率题模型一样，第(2)和第(3)小题的关键都在于弄清独立事件和条件概率的区别.P(B|A)与P(AB)的概率有本质的联系与区别，联系是事件A，B都已经发生，区别是样本空间不同：在P(B|A)中，事件A成为新的样本空间，在P(AB)中，样本空间仍为原样本空间.

以上3种方法对所有条件概率问题都适用吗？不一定.

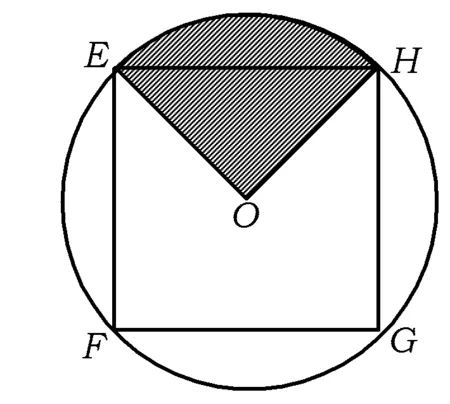
图1

例3如图1，四边形EFGH是以O为圆心、半径为1的圆内接正方形，将一颗豆子随机地扔到该圆内，用A表示事件“豆子落在正方形EFGH内”，B表示事件“豆子落在扇形OHE(阴影部分)内”，则(1)P(A)=______；(2)P(B|A)=______.

(2011年湖南省数学高考理科试题)

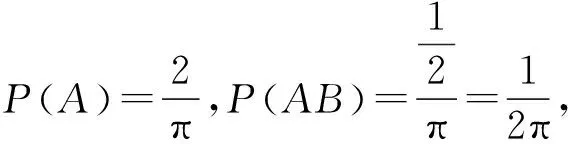
方法2(缩小样本空间)即落在正方形区域的面积与扇形中的正方形的面积之比，

例4根据以往的经验，某工程施工期间的降水量X(单位：mm)对工期的影响如表1所示：

表1 降水量对工期的影响

历年气象资料表明，该工程施工期间降水量X小于300，700，900的概率分别为0.3，0.7，0.9.求：

(1)工期延误天数Y的分布列；

(2)在降水量X至少是300的条件下，工期延误不超过6天的概率.

(2012年湖北省数学高考理科试题)

解(1)由已知条件和概率的加法公式知

P(X<300)=0.3,

P(300≤X<700)=P(X<700)-P(X<300)=

0.7-0.3=0.4,

P(700≤X<900)=P(X<900)-P(X<700)=

0.9-0.7=0.2,

P(X≥900)=1-P(X<900)=1-0.9=0.1,

从而Y的分布列如表2所示：

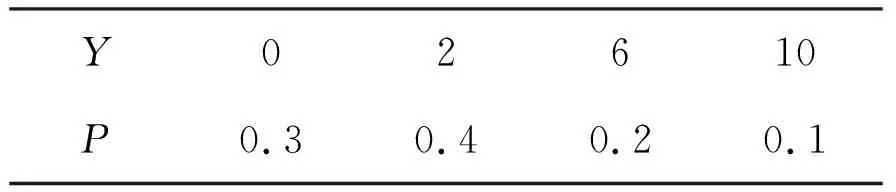
表2 Y的分布列

(2)由概率的加法公式得

P(X≥300)=1-P(X<300)=1-0.3=0.7.

又P(300≤X<900)=P(X<900)-P(X<300)=

0.9-0.3=0.6,

从而由条件概率，得

P(Y≤6|X≥600)=P(X<900|X≥300)=

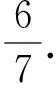
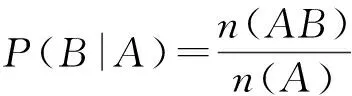
3 能力提升

例5某中学为了迎接即将在武汉市召开的世界中学生运动会，学生篮球队准备假期集训，集训前共有6个篮球，其中3个是新球(即没有用过的球)，3个是旧球(即至少用过1次的球)．每次训练，都从中任意取出2个球，用完后放回．

(1)设第1次训练时至少取到1个新球，第2次训练也取到1个新球的概率；

(2)在第1次训练时至少取到1个新球的条件下，求第2次训练时恰好取到1个新球的概率．

分析此题第(1)和第(2)小题仍然是独立事件与条件概率的区别，但特殊的是条件概率中“条件”变复杂了，要能够正确运用公式求解.

解(1)设“第1次训练时取到i个新球”为事件Ai(i=1,2,3),则

设“从6个球中任意取出2个球，恰好取到1个新球”为事件B，则“第2次训练时恰好取到1个新球”就是事件A1B+A2B，而事件A1B,A2B互斥，于是

P(A1B+A2B)=P(A1B)+P(A2B).

由条件概率公式，得

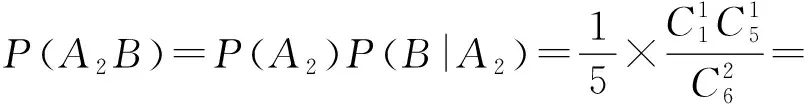
所以，第2次训练时恰好取到1个新球的概率为

(2)方法1设A=在第1次训练时至少取到1个新球，C=第2次训练时恰好取到1个新球,则在第1次训练时至少取到1个新球的条件下，第2次训练时恰好取到1个新球的概率为P(C|A).因为

又

所以

方法2设A=第1次训练时至少取到1个新球,C=第2次训练时恰好取到1个新球,则