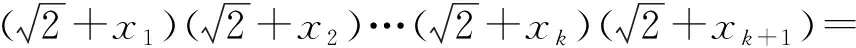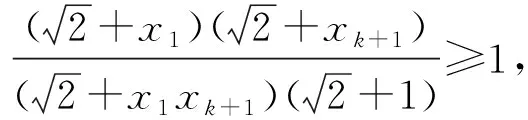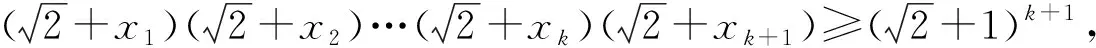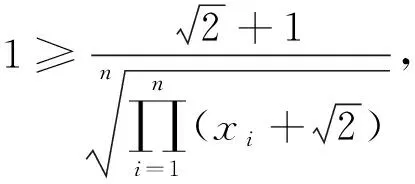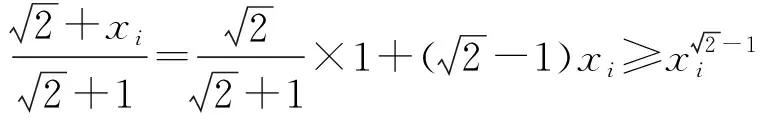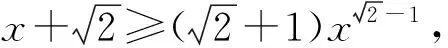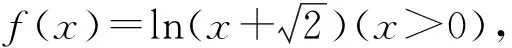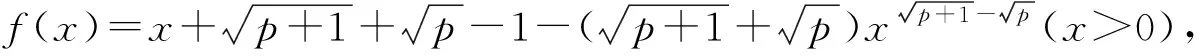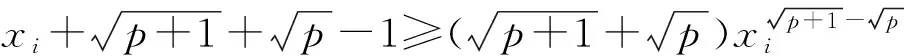2014年“北约”自主招生压轴题的证明与推广
2014-08-07常熟市中学江苏常熟215500
● (常熟市中学 江苏常熟 215500)
时光飞逝,转眼间一年一度的高校自主招生选拔考试已落下帷幕.纵观2014年“北约、华约、卓越”三大联盟的自主招生考试数学试题,无论是在知识方法,还是在试卷难度与解题技巧上都在向数学高考的模式理性回归.另外,在试题的命制上,三大联盟所推出的数学选拔试题都同高考试题一样,均遵循源于教材而高于教材的命题原则,且大大减少了高考以外的内容,从而使2014年的自主招生试题更贴近考生,更能公正、公平、有效地选拔优秀学生.正因如此,2014年三大联盟的自主招生数学考试很接地气,获得了社会各界和广大师生的一致好评.同时,也为以后高校自主招生选拔考试引领了全新的方向.2014年“北约”自主招生数学考试的压轴题就是一个源于教材而高于教材的不等式证明题.它结构简洁、内涵丰富,对学生的思维能力和代数推理能力提出了较高的要求,很好地起到了“北约”试题的选拔功效.以下笔者将给出该优美试题的7种证法并作推广,供读者在学习和研究时参考.
试题呈现若n个正数x1,x2,…,xn满足x1x2…xn=1,求证:
(2014年“北约”联盟理科试题第10题)

因此当n=2时,命题也成立.
(2)假设n=k时命题成立,即若正数x1,x2,…,xk满足x1x2…xk=1,则
当n=k+1时,由xi>0(i=1,2,…,k+1)且x1x2…xkxk+1=1可知这k+1个正数中至少有1个不小于1,至少有1个不大于1.不妨设0 又因为 即当n=k+1时,命题也成立. 由数学归纳法原理可知原命题成立. 评注本题是一个与自然数有关的命题,并注意到二元时是一个简单的柯西不等式,故采用数学归纳法应该是学生解答本题的首选.不过要顺利完成证明,还需具有较高的变形能力和归纳技巧. 证法2结合条件和应用n元均值不等式,分别可得 评注采用n元均值不等式证明此题,流畅飘逸,给人以美的享受.但需要学生具有敏锐的观察力和熟练的代数变形能力. 证法3利用柯西不等式的推广,得 评注证法3运用了柯西不等式的一个n次推广:若ai>0,bi>0,则 但因教材没有介绍,考纲中也未列入这个不等式,若采用此法来证明,应先证明这一结论才能得满分. 证法4由赫尔德不等式,得 评注由证法4可看出此不等式的本质是赫尔德不等式的一个应用,同时也说明柯西不等式的推广其本质就是赫尔德不等式. 证法5由xi>0(i=1,2,…,n),利用加权均值不等式,得 将这n个不等式相乘并注意到条件x1x2…xn=1,即证. 证法7考虑取对数,原命题等价于:若n个正数x1,x2,…,xn满足x1x2…xn=1,则 故原不等式成立. 现行的高中教材上有一个经典的不等式(1+a2)(1+b2)≥(1+ab)2,命题者匠心独运、深谋远虑,对这个熟知的不等式进行了n次推广.学生普遍感觉似曾相识,但要完成它的证明还是相当不易.它入口较宽,解法多样,能有效地检测和区分出学生的数学素养和解题能力,起到了全套试题的压轴功效.本题是一个源于教材而高于教材的典范,画出了2014年自主招生数学试题的一道靓丽风景. 最后,笔者受命题者思路的启发,给出这个优美试题的一个推广.