一道解析几何高考试题的题源探究与推广

●

(泉州市第五中学 福建泉州 362000)

●王志良

(安溪县第一中学 福建安溪 362400)

1 问题再现

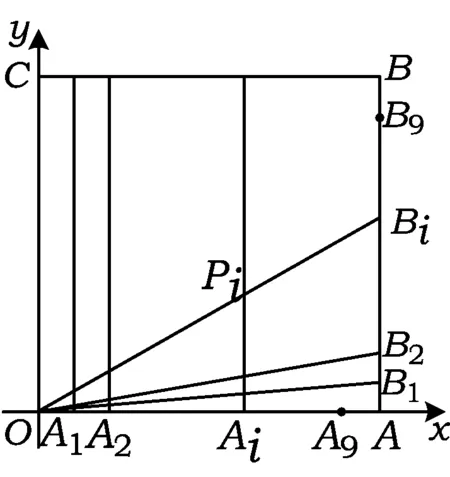
图1

题目

如图1，在正方形OABC中，O为坐标原点，点A的坐标为(10,0)，点C的坐标为(0,10)，分别将线段OA和AB十等分，分点分别记为A1,A2,…,A9和B1,B2,…,B9，联结OB1，过点A1作x轴的垂线与OBi交于点Pi(i∈N*,1≤i≤9)．

(1)求证：点Pi(i∈N*,1≤i≤9)都在同一条抛物线上，并求该抛物线E的方程；

(2)过点C作直线l与抛物线E交于不同的点M,N，若△OCM与△OCN的面积比为4∶1，求直线l的方程．

(2013年福建省数学高考试题)

本题主要考查抛物线的性质、直线与抛物线的位置关系等基础知识；考查运算求解能力、推理论证能力；考查化归与转化思想、数形结合思想、函数与方程思想．

在第(1)小题中，可以求得Pi(i∈N*,1≤i≤9)都在同一条抛物线上，且抛物线E的方程为x2=10y.我们知道，圆锥曲线在某些性质方面常常呈现出统一性，那么在椭圆和双曲线中是否存在和抛物线一样的性质呢？请先看本题在教材中的题源，结合题源，我们将对此性质进行进一步的探究.

2 题源探究

本题源于人教A版《数学(选修2-1)》第2章“圆锥曲线与方程”后的习题：

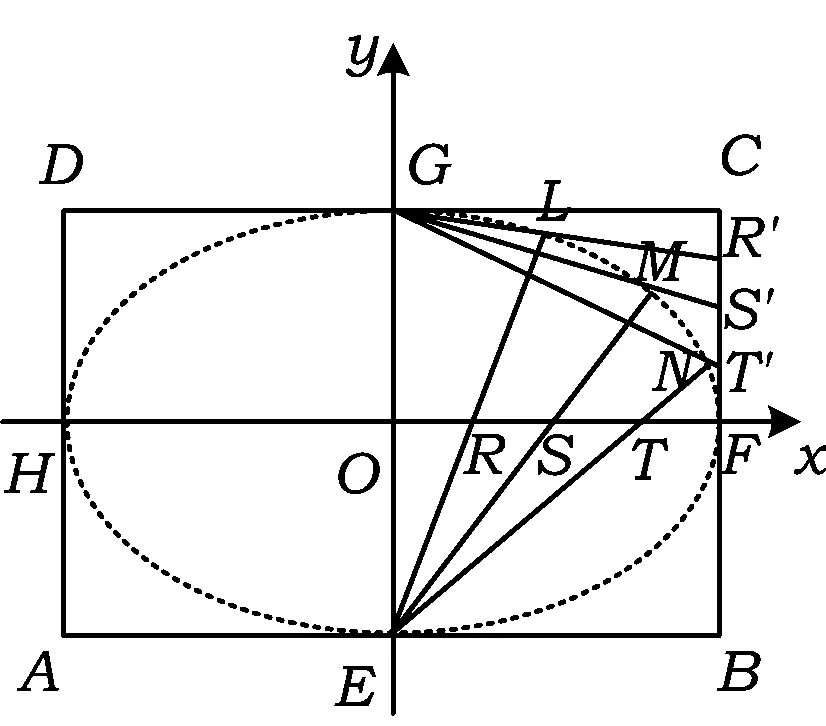
图2

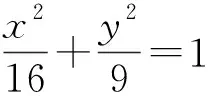
3 问题推广

圆锥曲线的一些性质往往表现出统一性，若将以上结论推广，可以得到以下命题：

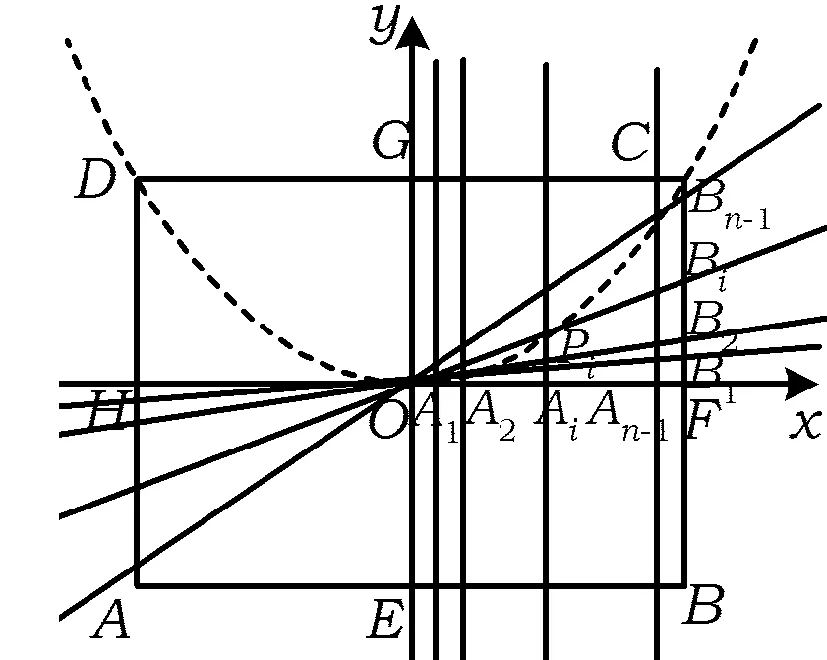
图3

命题1

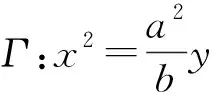
注：若a=b=2p，则抛物线的方程为x2=2py.

证明

过点Ai(i∈N*,1≤i≤n-1)且与x轴垂直的直线方程为

直线OBi的方程为

设Pi(x,y)，则

消去i，得

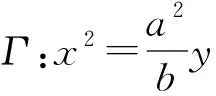
命题2

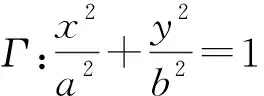
注：①当a=b时，曲线Γ为圆；②当a≠b时，曲线Γ为椭圆.

图4 图5

命题3

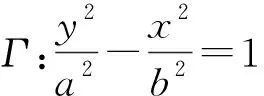
命题2与命题3的证明此处从略.在上述的3个命题中，通过构造整数分点，进而构造2个直线族，从而得到了一群“离散”的交点，此时，交点恰在相应的圆锥曲线上．那么，当我们更改命题中的条件，使得2个直线族的交点“连续”时，交点的轨迹是否正是相应的圆锥曲线呢？通过探究得到：

命题4

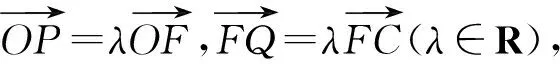
注：若a=b=2p，则抛物线的方程为x2=2py.

该命题的证明较为简单，可以参考以下命题5或命题6的证明，故此处从略.

图6 图7

命题5

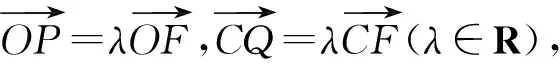
注：①当a=b时，点M的轨迹为圆；②当a≠b时，点M的轨迹为椭圆.

证明

由已知可得P(λa,0)，Q(a,(1-λ)b)，当λ≠0时，直线EP的方程为

直线GQ的方程为

设M(x,y)，则

消去λ，得

当λ=0时，易证直线EP与GQ的交点M亦满足方程

因此直线EP与GQ的交点M的轨迹为曲线Γ:

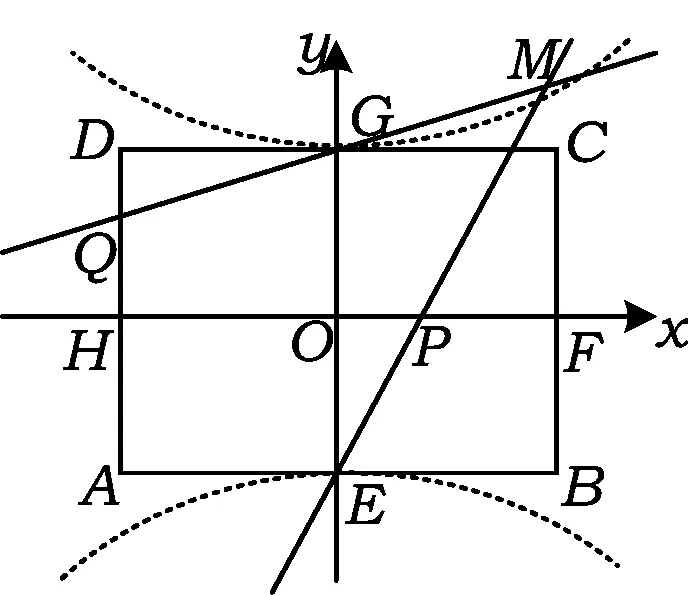
图8

命题6

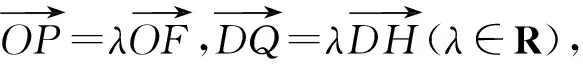
证明

由已知可得P(λa,0)，Q(-a,(1-λ)b)，当λ≠0时，直线EP的方程为

直线GQ的方程为

设M(x,y)，则

消去λ，得

当λ=0时，直线EP与GQ的交点M亦满足方程

因此直线EP与GQ的交点M的轨迹为双曲线Γ: