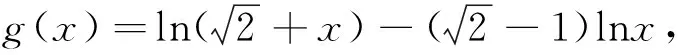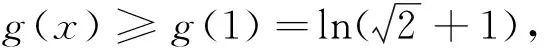解析并推广2014年“北约”自主招生不等式试题

●

(胜利第一中学 山东东营 257027)

证法6

题目

已知正实数x1,x2,…,xn满足x1x2…xn=1，求证：

证法1

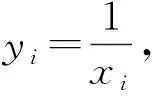
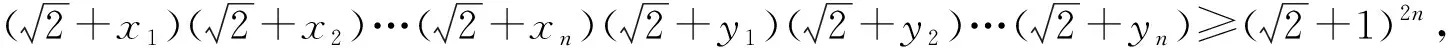
证法2

由AM-GM不等式知

(1)

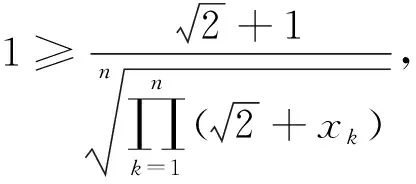
由平均值不等式得

证法4

(2)假设当n=k(k≥1)时不等式成立，即

则当n=k+1时，因为x1x2…xkxk+1=1，所以至少存在2个数，其中一个不大于1，另一个不小于1，不妨设xk≤1，xk+1≥1，从而(xk-1)(xk+1-1)≤0，则xk+xk+1≥1+xkxk+1.由x1x2…xk-1(xkxk+1)=1以及n=k的假设知

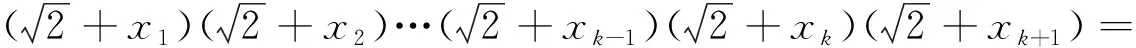
故当n=k+1时不等式也成立.

综合(1)(2)知，不等式对任意正整数n均成立.

证法5

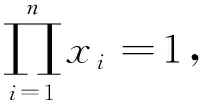
于是f(x)是凸函数.由琴生不等式得

证法6