一道伊朗竞赛题的再探究

●

(广东省珠海市实验中学高中部 519090)

题目

设a>0,b>0,c>0,a2+b2+c2+abc=4,求证：

a+b+c≤3.

(1)

(第21届伊朗数学奥林匹克竞赛试题)

笔者最近在竞赛教学中对该试题进行了一番探讨，感悟颇多！在此先给出简洁的证明，然后谈谈对该试题的一些发散式探究，最后给出一组相关的数学竞赛试题，希望对读者起到抛砖引玉的作用.

1 简证

证法1

注意到

4=a2+b2+c2+abc≥

2ab+c2+abc=ab(2+c)+c2,

于是

ab≤2-c.

由抽屉原则知3个正实数a,b,c中必有2个不大于或不小于1.不妨设正实数a,b满足(a-1)(b-1)≥0,则

ab≥a+b-1，

从而

2-c≥ab≥a+b-1,

故

a+b+c≤3.

证法2

令a=2p,b=2q,c=2r,则条件“a2+b2+c2+abc=4”变形为

p2+q2+r2+2pqr=1，

cos2A+cos2B+cos2C+2cosAcosBcosC=1,

对比p2+q2+r2+2pqr=1，不妨设p=cosA,q=cosB,r=cosC,则式(1)等价于

此式由琴生不等式即证.

注

证法2中用到一个常用恒等式“cos2A+cos2B+cos2C+2cosAcosBcosC=1”.事实上，在△ABC中，A+B+C=π,且

cos2A= cos2(B+C)=(cosBcosC-sinBsinC)2=

cos2Bcos2C+(1-cos2B)(1-cos2C)-

2sinBsinCcosBcosC=

1-cos2B-cos2C+2cosBcosC(cosBcosC-

sinBsinC)=

1-cos2B-cos2C+2cosBcosCcos(B+C)=

1-cos2B-cos2C+2cosAcosBcosC,

故

cos2A+cos2B+cos2C+2cosAcosBcosC=1.

2 发散式探究

探究1

设a>0,b>0,c>0,a2+b2+c2+abc=4,则abc≤1.

证明

探究2

设a>0,b>0,c>0,a2+b2+c2+abc=4,则a+b+c≥ab+bc+ca.

证明

注意到

(a+b+c)2≥ 3(ab+bc+ca)≥

(a+b+c)(ab+bc+ca),

故

a+b+c≥ab+bc+ca.

探究3

设a>0,b>0,c>0,a2+b2+c2+abc=4,则a2+b2+c2≥3.

证明

注意到abc=4-(a2+b2+c2)≤1,故a2+b2+c2≥3.

探究4

设a>0,b>0,c>0,a2+b2+c2+abc=4,则

证明

注意到

而

a2+b2+c2+abc=4≥a2+2bc+abc,

于是0≥a2-4+bc(2+a)=(2+a)(a-2+bc),

得

0≥a-2+bc，

即

2≥a+bc,

亦即

2a≥a2+abc.

同理可得

2b≥b2+abc,2c≥c2+abc,

因此2(a+b+c)≥ (a2+b2+c2+abc)+2abc=

4+2abc,

故

a+b+c≥2+abc.

又由式(1)可知3≥a+b+c，从而

探究5

设a>0,b>0,c>0,a2+b2+c2+abc=4,则

2+abc≥ab+bc+ca≥3abc≥(a+b+c)abc.

证明

注意到(a+b+c)2≥3(ab+bc+ca)和ab+bc+ca≤3,于是

abc(a+b+c)=ab·bc+bc·ca+ca·ab=

ab+bc+ca,

因此

ab+bc+ca≥abc(a+b+c).

而3≥a+b+c,故

ab+bc+ca≥3abc≥abc(a+b+c).

由题知a,b,c中一定有且只有2个数都不大于1或者不小于1，不妨设这2个数为a,b,则

c(a-1)(b-1)≥0,

即

bc+ac≤abc+c.

而

a2+b2+c2+abc=4≥2ab+c2+abc,

故

ab(2+c)≤4-c2,

即

ab≤2-c，

从而

ab+bc+ca≤2-c+abc+c=2+abc.

综上可得,

2+abc≥ab+bc+ca≥3abc≥(a+b+c)abc.

注

由探究5的结果“2+abc≥ab+bc+ca≥3abc≥(a+b+c)abc”得“2+abc≥3abc”，即“abc≤1”，即为探究1.探究5可看作是探究1的一个加强.而“3abc≥(a+b+c)abc”可以看作是式(1)的一个等价形式.

探究6

设a>0,b>0,c>0,a2+b2+c2+abc=4,则

ab+bc+ca≥3abc≥(a+b+c)abc.

证明略.

需要说明的是，在△ABC中有如下结论(限于篇幅，请读者自行证明)：

(1)cos2A+cos2B+cos2C+2cosAcosBcosC=1;

即

(4-a2)(4-b2)(4-c2)≤27.

类似地，在条件“a>0,b>0,c>0,a2+b2+c2+abc=4”下新的探究,读者可根据相关的三角不等式进行运算,在此不再一一赘述.

3 相关赛题

事实上，与条件“a>0,b>0,c>0,a2+b2+c2+abc=4”相关的竞赛试题在各级各类数学竞赛中屡见不鲜.由式(1)证法2可进行三角代换a=2cosA,b=2cosB,c=2cosC,从而可以将难以下手的代数问题转化为三角函数问题轻松地解决.

例1

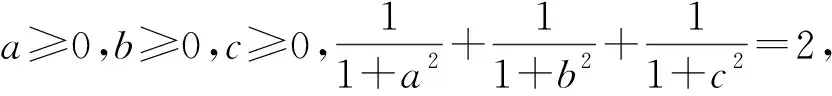
(2007年美国数学奥林匹克竞赛国家集训队试题)

证明

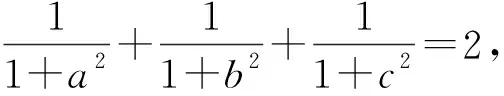
a2b2+b2c2+c2a2+2a2b2c2=1.

令p=ab,q=bc,r=ca,则“a2b2+b2c2+c2a2+2a2b2c2=1”可变形为

p2+q2+r2+2pqr=1,

从而待证式等价于

令p=cosA,q=cosB,r=cosC,结合琴生不等式知

例2

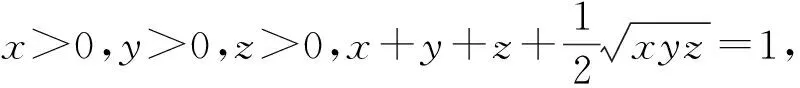
(2006年全国高中数学联赛河南省预赛试题)

证明

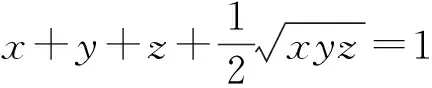
p2+q2+r2+2pqr=1,

从而待证式等价于

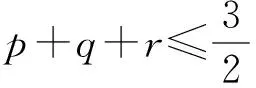
例3

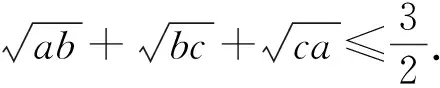
(2005年罗马尼亚国家队数学奥林匹克竞赛

预选试题)

证明

注意到条件“ab+bc+ca+2abc=1”可以转化为

x2+y2+z2+2xyz=1，

例4

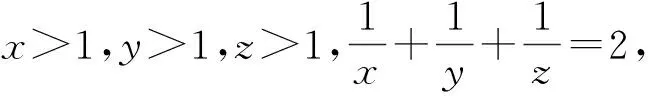
(1998年伊朗数学奥林匹克竞赛试题)

证明

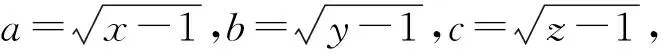
即

a2b2+b2c2+c2a2+2a2b2c2=1.

令p=ab,q=bc,r=ca,则“a2b2+b2c2+c2a2+2a2b2c2=1”可变形为

p2+q2+r2+2pqr=1，

从而待证式等价于

即

亦即

显然由例1即可知待证式成立.