柯西不等式的变式的应用

●

(抚顺市第一中学 辽宁抚顺 113001)

无论是高考试题、自主招生试题，还是数学征题、奥林匹克竞赛试题，都有一个显著的特点：无论这些试题外表多么新奇、实质内容多么深奥，它们的“根”都“植在”我们天天见面、但却时常被忽视的教材中.教材是一座宝藏，里面蕴涵着取之不尽、用之不竭的资源.“研究教材、吃透教材、整合教材、开发教材”才是从容应对各类试题最有效的方法与策略.

笔者在此例谈选修教材中柯西不等式的变式：若xi,yi∈R+,则

例1

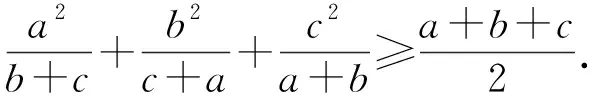
(第2届世界“友谊杯”数学竞赛试题)

证明

由柯西不等式变式，得

评注

这道世界名题经历几十年的洗礼，依然是数学爱好者津津乐道的一道经典试题，其证明方法多达几十种.上述证法简洁明了，是该变式的一个简单应用，上述命题可推广为：

若ai∈R+(i=1,2,3,…,n)，则

有趣的是，若把例1中的a,b,c分别换成bc,ca,ab就得到第36届IMO试题：

例2

(第36届IMO试题)

证明

由abc=1，原不等式经适当的恒等变形，得

又由柯西不等式变式，得

评注

上述证明过程简洁流畅，一气呵成.正如爱因斯坦所言：“美，本质上终究是简单性.”

例2可推广为:若a,b,c是正数，n∈N+，且abc=1，则

例3

(《数学教学》数学问题488)

证明

由柯西不等式变式，得

评注

原题的解答过程较为复杂，上述构思自然流畅，美不胜收.

例4

(《数学通报》问题1 724)

证明

评注

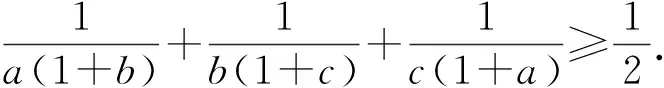
例5

(《中等数学》数学奥林匹克问题之163(高中))

推广1

推广2

评注

例6

(2008年南开大学自主招生试题)

由柯西不等式变式，得

评注

上述证明极其简洁巧妙，构造分母“1”让人拍案叫绝.正如克莱因所言：“一个精彩巧妙的证明，精神上似乎一首诗.”

该推广恰为2011年甘肃省高中数学竞赛预赛试题.

例7

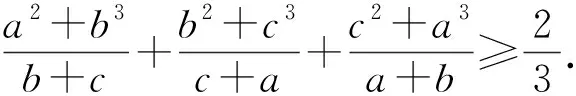
证明

由柯西不等式变式,得

(1)

(2)

式(1)+式(2),即得证

评注

例7在证明过程中3次用到柯西不等式的变式，可谓将其展示得淋漓尽致、入木三分.

例8

(2009年韩国数学奥林匹克竞赛试题)

证明

原不等式经过适当的恒等变形，得

又由柯西不等式变式，得

评注

在例1～例7中，由于篇幅限制笔者给出较常见的推广.以下笔者从线性系数、幂数、元数这3个方面入手，对例8进行一般性的推广：

(1)线性化推广：若a,b,c,s,t∈R+，则

(2)幂数一般化推广：若a,b,c∈R+，则

(3)元数一般化推广：若ai∈R+(i=1,2,3,…,n)，则

(4)结合(1)，(2)更一般化推广：若a,b,c,s,t∈R+，则

(5)结合(1),(3)更一般化推广：若s,t,ai∈R+(i=1,2,3,…,n)，则

(6)结合(2),(3)更一般化推广：若ai∈R+(i=1,2,3,…,n)，则

(7)结合(1),(2),(3)最终推广：若s,t,ai∈R+(i=1,2,3,…,n)，则

尽管这些竞赛试题难度大，甚至无从入手，但并非高不可攀.其实，这些试题并非空穴来风，源于教材而高于教材.在各类的考试中，很多试题是在教材的概念、公式、定理、例题、习题的基础上演变而来.因此，最大程度的开发、利用、整合教材是从事数学研究的重中之重.数学难也难在这，数学美也就美在这，这正是新课改的精髓所在，也是笔者撰写本文的目的.

参 考 文 献

[1] 王淼生.数学美本质上终究是简单[J].中学数学教学参考，2013(3)：29-30.