一类非线性Choquard 方程解的存在性*

周庆翡, 沈自飞

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

0 引 言

本文研究一类非线性Choquard 方程

(1)

当a(x)=1,a(y)=1,p=2,μ=1时,方程(1)即为

(2)

方程(2)是由物理学家Choquard在等离子体的Hartree-Fock理论中首先提出的.文献[1]利用临界点理论证明了方程(2)非平凡解的存在性;文献[2]证明了方程(2)在V(x)=1时方程

(3)

基态解的存在性,且该基态解具有非退化性;文献[3]利用极大极小值方法证明了方程

(4)

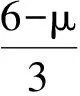
(5)

解的存在性;文献[5]利用变分方法证明了方程

(6)

在H1(RN)中存在正的孤立解.

本文在R3中假设连续位势函数V(x)和连续有界函数a(x),a(y)满足如下条件:

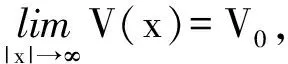
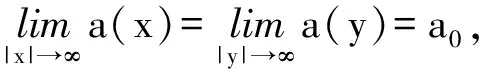
本文的主要结论是:

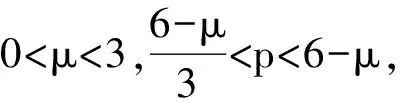
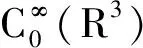
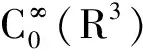
▽u|2+V0|u|2)dx.

Hilbert空间D1,2(R3)={u∈L2*(R3):|▽u|∈L2(R3)}中的范数被定义为

Ls(R3)空间中的范数是指

1 引 理

为了证明定理1,首先考虑方程(1)的极限形式

(7)

解的存在性,为此需要下面引理:

引理1[6]若V(x)满足条件(f1),则Hilbert空间E到H1(R3)空间的嵌入是连续的.

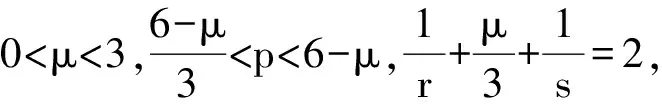
方程(7)的能量泛函为

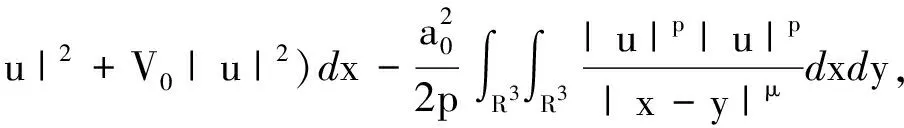
且方程(7)的弱解u即为泛函J∞(u)在H1(R3)上的临界点.而方程(1)相应的变分泛函为

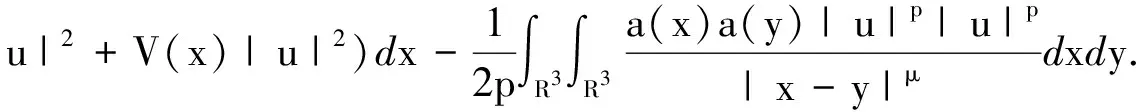
显然,J(u)∈C1(E,R).

定义1对于泛函J(u)∈C1(E,R),称E中的序列{un}n≥1满足(PS)C条件,如果存在常数C,使得当J(un)→C, J′(un)→0时,{un}n≥1存在一子序列{unk}k≥1在E中强收敛.

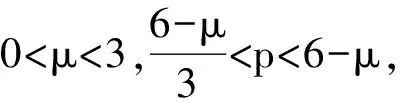
证明 首先证明:若满足(PS)C条件的序列{un}存在,则序列{un}在H1(R3)上有界.事实上,由假设有

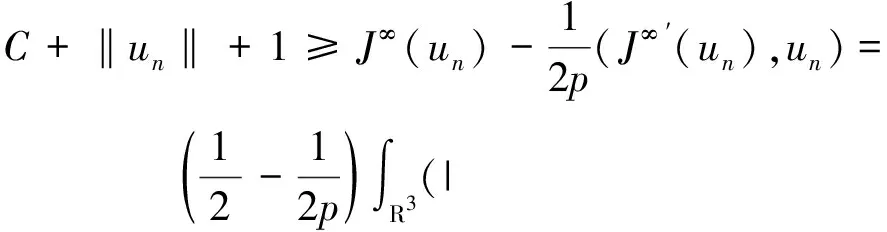
所以序列{un}在H1(R3)上有界,且C>0.

下面证明满足(PS)C条件的序列{un}的存在性.事实上,由于序列{un}在H1(R3)中有界,从而存在收敛子列,不妨仍记为{un},当n→∞时,有

(8)

由(PS)C条件的定义可知,要证明序列{un}为泛函J∞(u)的满足(PS)C条件的序列,只需要证明J∞(un-u)→C-J∞(u),J∞′(un-u)→ 0成立.事实上,由计算可得

J∞(un)-J∞(u)+Sn+o(1).

(9)

式(9)中,

(10)

从而由非局部的Brezis-Lieb引理[8]可得Sn→0.因此,J∞(un-u)→ C-J∞(u).

又对任意的φ∈H1(R3),当‖φ‖≤1时,有

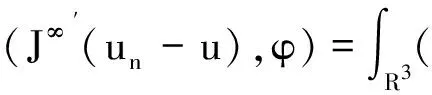
(11)

式(11)中,

(12)

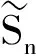
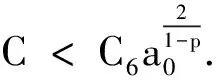
即

由于J∞′(wn)→ 0,利用Hardy-Littlewood-Sobolev不等式有

(13)

又由Hölder不等式可得

(14)

即

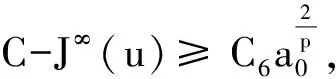
引理4[7]在Hilbert空间H1(R3)上恒有

下面证明 J∞满足山路引理的几何条件.

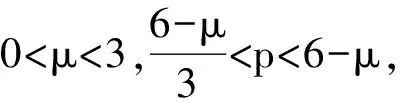
1)J∞(0)=0,且存在α,ρ>0,使得对于‖u‖=ρ,有J∞(u)≥α;

2)存在e>0,使得当‖e‖>ρ时,有J∞(u)<0.

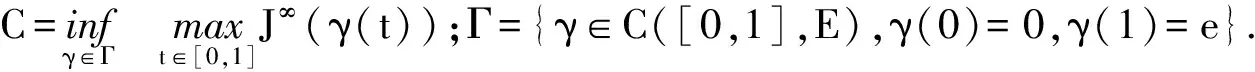
证明 1)显然,J∞(0)=0成立.由Hardy-Littlewood-Sobolev不等式可得

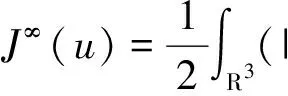
(15)

又因为p>1,所以存在‖u‖=ρ,使得J∞(u)≥α成立.

2)由引理4可得

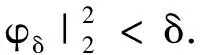
取e=φδ,可得

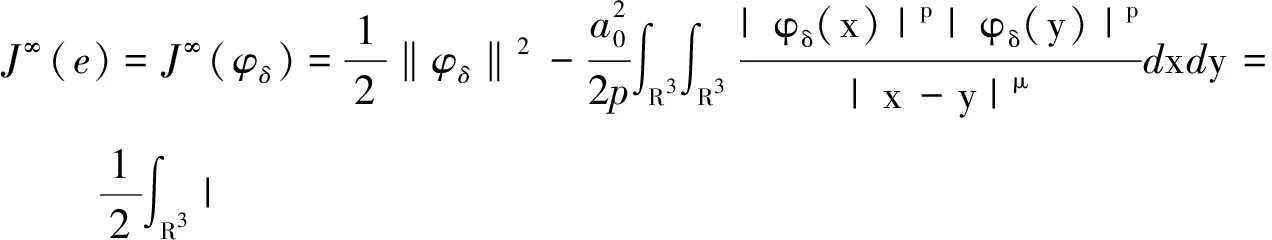
(16)

为了证明定理1,还需要下面的引理.

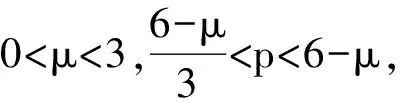
其中,Bk={x∈R3| |x|≤k}.

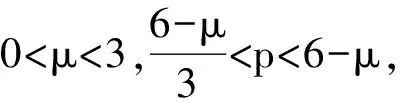
证明 因为‖un-u‖→0,所以由Sobolev嵌入的局部紧性可知,对于任意的 r>0,

(17)

关于‖φ‖≤1一致成立.由引理6可知,对任意的ε>0,存在γε>0,当r≥γε时,有

且序列{un}在H1(R3)上有界.

又由Hölder不等式和a(y)的有界性可知

(18)

而由引理6和式(18)有

(19)

由ε的任意性可知结论成立.引理7证毕.

记

(22)

因而有下面的引理:

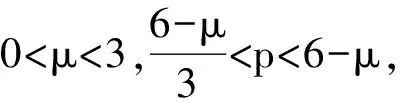
证明 由S∞,S′的定义和条件(f1),(f2)可知S′≤S∞.

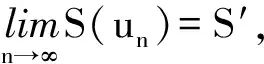
由引理1可知,E到H1(R3)的嵌入是连续的,且序列{un}在H1(R3)上有界,从而存在一个收敛子列,不妨仍记为{un},当n→∞时,有

因此,在E上有un⇀u , 且

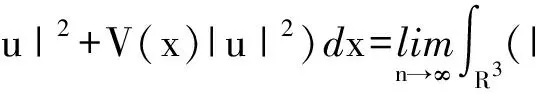
(23)

由假设有

(24)

而当

时,式(24)与引理7矛盾.因此,存在u∈E{0},有S(u)=S′.引理8证毕.

2 定理的证明

由引理1～5可知,Choquard方程(1)的极限形式(7)存在弱解u.由引理6～8有

S(u)=inf{S(v):v∈E{0}},

即存在u∈E{0},使得

也即方程(1)存在非平凡弱解.定理1证毕.

参考文献：

[1]Lions P L.The Choquard equation and related questions[J].Nonlinear Anal,1980,4(6):1063-1072.

[2]Wei Juncheng,Winter M.Strongly interacting bumps for the Schrödinger-Newton equations[J].J Math Phys,2009,50(1):1-22.

[3]Zhang Zhengjie.Existence of a nontrivial solution for Choquard′s equation[J].Acta Mathematica Scientia,2006,26B(3):460-468.

[4]Yang Minbo,Ding Yanheng.Existence of solutions for singularly perturbed Schrödinger equations with nonlocal part[J].Communications on Pure and Applied Analysis,2013,12(2):771-783.

[5]Moroz V,Schaftingen J V.Groundstates of nonlinear Choquard equations:existence,qualitative properties and decay asymptotics[J].J Funct Anal,2013,265(2):153-184.

[6]Ding Yanheng,Lin Fanghua.Solutions of perturbed Schrödinger equation with critical nonlinearity[J].Calculus of Variations and Partial Differential Equations,2007,30(2):231-249.

[7]Lieb E,Loss M.Analysis(Graduate studies in mathematics)[M].2nd ed.Rhode Island:AMS,2001:346.

[8]Ackermann N.On a periodic Schrödinger equation with nonlocal superlinear part[J].Math Z,2004,248(2):423-443.

[9]Ding Yanheng,Wei Juncheng.Semiclassical states for nonlinear Schrödinger equations with sign-changing potentials[J].J Funct Anal,2007,251(2):546-572.