低维冷原子体系中基于密度泛函理论严格解的呼吸模研究*

卫福霞, 高先龙

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

0 引 言

随着现代冷却技术的逐渐成熟，人类已经可以制备出不同类型的束缚势，通过调节外部束缚势使系统成为低维.在系统的z方向加一个比较平缓的势场，而在xy方向加上比较强的势场，使粒子在xy方向上的运动被限制在零点振动，这样可制备准一维束缚量子气体.一维量子气体的许多物理性质和现象是三维体系所不具有的.例如，一维体系具有Luttinger液体的性质，而三维体系由Landau费米液体所描述.近几年，对一维量子气的研究已由玻色气体扩大到费米子以及玻色费米混合系统,例如：MIT和Rice大学研究组进行的非平衡费米气体实验[1]；Recati等[2]对束缚在细长谐振势中双组分费米气体性质的研究.在弱耦合和强耦合限制下，这些研究者把Luttinger哈密顿量和系统的微观参数联系起来[3]，从而描述气体的低能性质.一维体系由于强关联性质的相互作用和Luttinger液体的性质，其在冷原子体系中的实现对凝聚态物理中的相关研究具有十分重要的作用.

均匀体系Gaudin-Yang模型[4-5]的一维费米气体可以精确求解，这为我们的研究提供了一些借鉴.冷原子实验中往往还有一个谐振势，从而使得体系是非均匀的.对于非均匀双组分费米气体的研究往往以局域密度近似(LDA)的平衡方程为基础，用均匀体系的化学势代替非均匀体系的化学势，进而求出平衡系统的密度分布以及呼吸模频率.由于局域密度近似是一个平均场结果，故求出的是近似解.而对于有限系统，LDA的近似结果需要作出检验，对于基于LDA的一些物理量的计算，也要从不同的角度予以检验.本文利用密度泛函理论(DFT)在某些参数范围内求出了更为准确的基态密度分布，并用该基态密度分布进一步求出呼吸模.

1 一维无极化费米气体的物理模型

本文主要讨论的是Gaudin-Yang连续模型，该模型由Gaudin[4]和Yang[5]分别提出,其中，文献[4]求解的是吸引相互作用模型，而文献[5]求解的是排斥相互作用模型.冷原子体系中一维自旋费米气体的哈密顿量为

(1)

式(1)即为有束缚势的非均匀Gaudin-Yang模型，不能解析求解.其中:N,g1D,ωz分别为总粒子数、相互作用和谐振势频率;N=N↑+N↓.为了计算呼吸模频率，利用求和法则

(2)

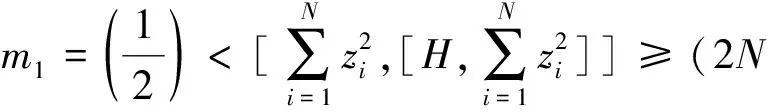
(3)

略去二阶项可得

(4)

令ε=-mωzΔωz，当Δωz很小时，则可得到

(5)

代入式(2)可得呼吸模频率公式

(6)

(7)

相互作用常采用下列方式无量纲化:

(8)

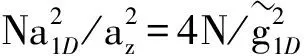
在外势的频率上作微扰，可以研究集体激发.集体激发不仅是超流原子气体元激发的主要形式，也是玻色-爱因斯坦凝聚(BEC)在低温下的最基本的激发模式，它是描述相互作用多体系统在外加束缚势中的集体振荡行为.现在许多实验都对超流原子气体中的集体激发有研究，并且取得了很好的结果.在集体激发的研究中，振荡频率的研究是必不可少的，它对于了解凝聚体的基态、超流特性和热力学性质，揭示非均匀量子体系中原子间相互作用性质和探索超冷量子气体的超流特性均有重要意义.除此之外，无极化条件下，它可以用来检验实验上是否获得新的量子气体和标度不同状态之间的转换[6-8].极化条件下，它可以用来标度不同的量子相[9-10].

2 研究方法

2.1 局域密度近似(LDA)方法

在谐振势中，当外势中存在大量费米子时，局域密度近似是一个比较准确的近似方法，结合均匀费米气的Bethe-ansatz解，可以得到当N≫1时系统的基态性质，利用局域密度近似并根据非均匀气体的局域平衡条件可以确定化学势，平衡条件为

2.2 密度泛函理论(DFT)方法

用LDA算出的是平均场结果是一个近似解.下面用DFT来精确求解基态密度分布.nGS(z)可以通过求解Kohn-Sham(KS)方程得到

(10)

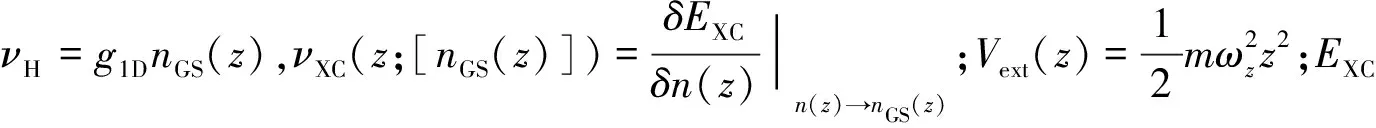
|φα(z)|2.

(11)

3 数值结果

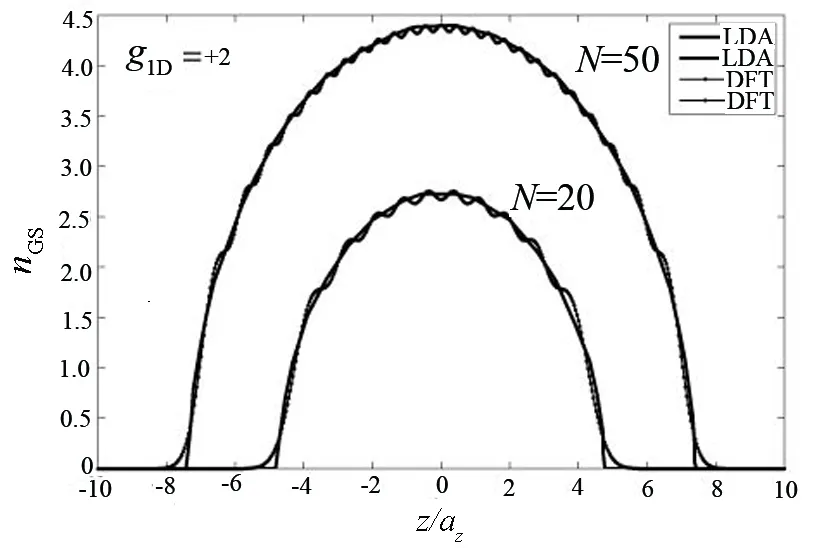
利用局域密度近似和密度泛函理论，借助式(9)～式(11)可得到无极化费米气体在外势中的密度分布情况.

图1给出了谐振势中双组分费米气体的密度分布nGS(z).它是以z/az为函数，其中相互作用强度分别为g1D=+2(见图1(a))和 g1D=-2(见图1(b)).均给出粒子总数N=20和50这2种情况.图1列出了LDA(实线)和DFT(点线)的结果作为比较.图1(a)是排斥相互作用的结果，图1(b)是吸引相互作用的结果.由图1中的密度分布结果可以看出，局域密度近似结果是一个光滑的曲线，是一种近似平均解，密度泛函理论结果反映了正确的Friedel振荡，是精确的密度分布[11].当粒子数不是很大时(如N～100，为实验中所用的粒子数)，DFT给出的结果更为可靠，它正确反映了密度分布.对于吸引相互作用，密度分布的振荡更为明显，此振荡行为对呼吸模的贡献是不可忽略的.下面笔者将用更为精确的密度分布求出呼吸模并与LDA的结果作比较.

(a) (b)

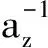
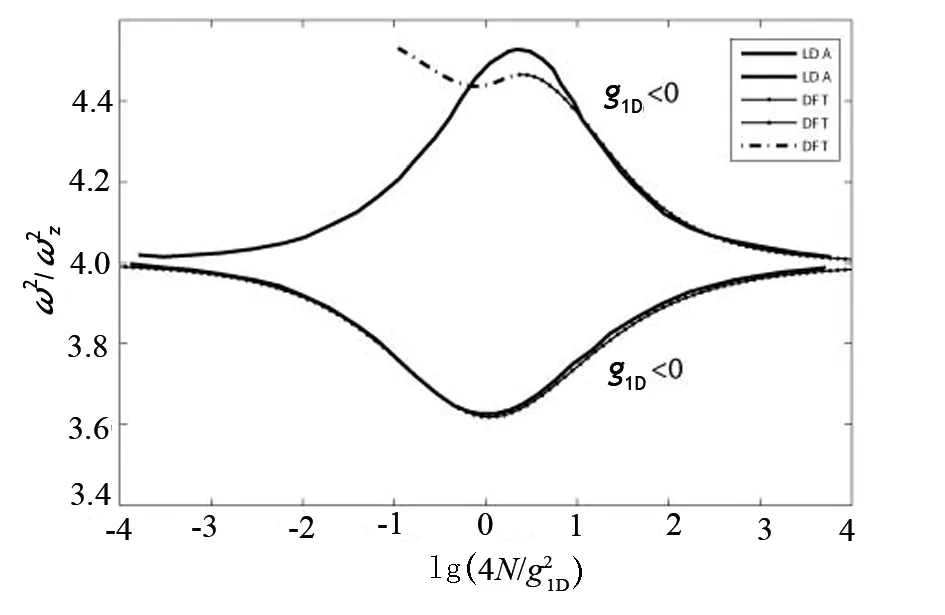
图2 谐振势中双组分费米气体的呼吸模

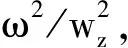
4 结 论

基于Bethe-ansatz解的密度泛函和局域密度近似，求解了谐振势中自旋双组分费米气体的呼吸模，可以得到如下结果：局域密度近似和密度泛函理论2种方法得到的密度分布有很大的不同，局域密度近似得到的密度分布的结果是光滑的曲线，是一种近似平均解，而密度泛函得到的是振荡的曲线，是精确的密度分布，从而能够精确地求解呼吸模.对于排斥相互作用，密度分布的微小振荡使呼吸模结果略小于局域密度近似结果；对于弱吸引相互作用，密度分布更为振荡，使呼吸模结果和局域密度近似的结果有较大的不同；对于强吸引相互作用，密度分布过于振荡，从而使呼吸模结果发散，不再准确.

参考文献：

[1]Partridge G B，Li Wenhui,Liao Y A,et al.Deformation of a trapped Fermi gas with unequal spin populations[J].Phys Rev Lett，2006，97 (19):190407.

[2]Recati A，Fedichev P O，Zwerger W，et al.Spin-charge separation in ultracold quantum gases[J].Phys Rev Lett，2003，90(2):020401.

[3]Astrakharchik G E，Blume D，Giorgini S，et al.Interacting fermions in highly elongated harmonic traps[J].Phys Rev Lett，2004，93(5):050402.

[4]Gaudin M.Un systeme a une dimension de fermions en interaction[J].Phys Rev A，1967,24(1):55-56.

[5]Yang Zhenning.Some exact results for the many-body problem in one dimensional with repulsive delta-function interaction[J].Phys Rev Lett，1967，19(23):1312-1315.

[6]Astrakharchik G E，Giorgini S.Quantum Monte Carlo study of the three-to one-dimensional cossover for a trapped Bose gas[J].Phys Rev A，2002，66(6):053614.

[7]Astrakharchik G E，Combescot R，Leyronas X，et al.Equation of state and collective frequencies of a trapped Fermi gas along the BEC-unitarity crossover[J].Phys Rev Lett，2005，95(4):030404.

[8]Astrakharchik G E，Boronat J，Casulleras J，et al.Equation of state of a Fermi gas in the BEC-BCS crossover：a quantum monte carlo study[J].Phys Rev Lett，2004，93(20):200404.

[9]Hu Hui，Liu Xiaji，Drummond P D.Phase diagram of a strongly interacting polarized fermi gas in one dimension[J].Phys Rev Lett，2007，98 (7):070403.

[10]Liu Xiaji，Hu Hui.Finite-temperature excitations of a trapped Bose-Fermi mixture[J].Phys Rev A，2003，68(3):033613.

[11]Gao Xianlong，Polini，Asgari R,et al.Density-functional theory of strongly correlated Fermi gases in elongated harmonic traps[J].Phys Rev A，2006，73(3):033609.