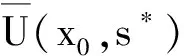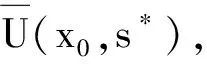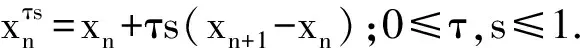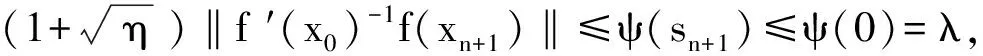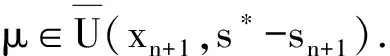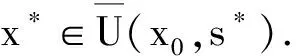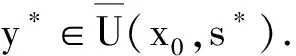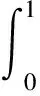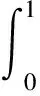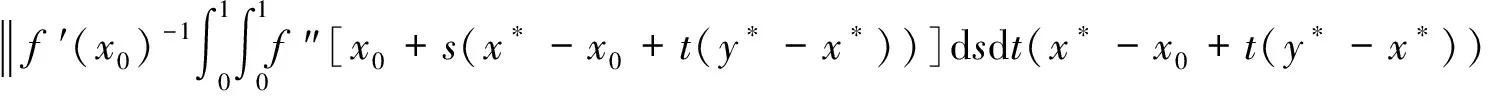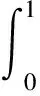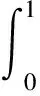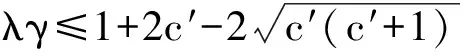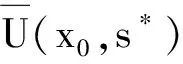非精确Newton法的半局部收敛性*
2014-08-06何金苏沈卫平
王 铭, 何金苏, 沈卫平
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
0 引 言
Banach空间中非线性算子方程
f(x)=0
(1)
的求解问题在数学理论及应用领域上有着较为广泛的应用.其中, f是从实的或复的Banach空间X的某个凸区域D到同型空间Y的连续Fréchet可微的非线性算子.通常在求解非线性方程(1)时,最常用的方法是Newton法,具体的迭代公式为
xn+1=xn-f′(xn)-1f(xn).
(2)
关于Newton法的收敛性分析通常可以分为2种类型:局部收敛性分析和半局部收敛性分析.局部收敛性分析是指先假设方程(1)的解x*存在,然后找到以x*为球心的一个邻域D,使得式(2)产生的序列在D内收敛[1-3].半局部收敛性分析则在没有假定方程组解存在的情况下,只根据初始近似x0满足的局部条件,就可以确保迭代序列的收敛性[1-4].在Newton法的半局部收敛性分析所得的结果中,最为著名的是Kantorovich定理[5],它为有界的二阶可导算子f "或者一阶可导Lipschitz连续算子提供了简单易懂的收敛准则.另外一个重要的定理是Smale′sα理论[6].至于利用优序列的方法考虑Newton法的收敛性[1-2,4,6],王兴华等[2]找到了最好的α判据,彻底改进了Smale′sα理论.而且,文献[6]引进了γ-条件,再次讨论了α判据,对Smale的点估计理论作了推广.
由式(2)知,使用Newton法求解方程(1)时,每步迭代都需要精确地求解方程
f′(xn)(xn+1-xn)=-f(xn).
(3)
从实际计算角度看,有时会使得Newton法无效,尤其当f ′(xn)很大且稠密时.但可采用线性迭代求解方程(3)的近似解,不用直接精确地求解方程(3),这样可以大大减少计算量.这种方法称为非精确Newton法.通常,非精确Newton法具有如下形式:
算法1给定初始近似x0,令n=0,1,…,开始执行如下步骤,直到序列收敛:
1)设rn为残差而xn为迭代值,求解sn,使其满足
f′(xn)sn=-f(xn)+rn;
2)xn+1=xn+sn;
3)令n=n+1,重新返回步骤1.
其中,{rn}是Y中的序列.
非精确Newton法的收敛性取决于{rn}的选择,一般情况下,条件不同,残差的选择也会有所差异.关于非精确Newton法的局部收敛性,文献[7]给出了最基本的结果.Argyros[8]在文献[7]的基础上,假设f "满足Lipschitz条件,分析了非精确Newton法的局部收敛性.文献[9]用仿射不变条件‖f ′(xi)-1ri‖≤vi‖f ′(xi)-1f(xi)‖(i=0,1,…)替代文献[8]中的条件‖rn‖≤ηn‖f(xn)‖,使得非精确Newton法亦具有仿射不变性.
至于半局部收敛性分析,文献[10]在假设f ′(x)满足Lipschitz连续下,采用控制‖f ′(x0)-1rn‖≤‖f ′(x0)-1f(xn)‖ηn分析了非精确Newton法的半局部收敛性.文献[11]为使改进的非精确Newton法具有仿射不变性,条件和控制分别选用‖f ′(y)-1(f ′(x+t(y-x))-f ′(x))‖≤L‖y-x‖和‖rn‖≤vn‖f ′(xn)-1f(xn)‖.文献[12]分析了在γ-条件[3]下非精确Newton法的半局部收敛性,同时给出了Smale型收敛准则,首次采用满足如下条件的残差{rn}:
(4)
本文采用满足式(4)的残差控制{rn},通过引入中心γ0-条件和γ-条件,得到了比文献[12]更精确的误差估计及更优的半局部收敛性定理.
1 预备知识
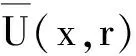
首先,引入γ-条件[3]及中心γ0-条件.
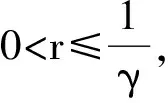
(5)
则称f关于x0在U(x0,r)⊆X上满足γ-条件.
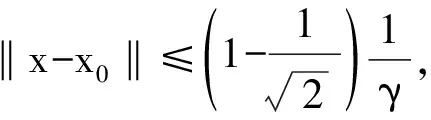
(6)
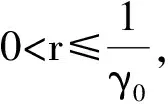
(7)
则称f关于x0在U(x0,r)上满足中心γ0-条件.
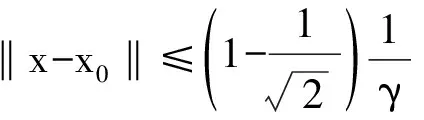
(8)
由定义2知,γ0≤γ.
下面给出证明非精确Newton法半局部收敛性所需要的相关结果.
为方便起见,令
(9)
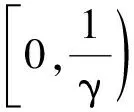
(11)
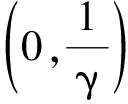
p*≥r*.
(12)
证明 由ψ和φ的定义知
ψ(t)≤φ(t);
(13)
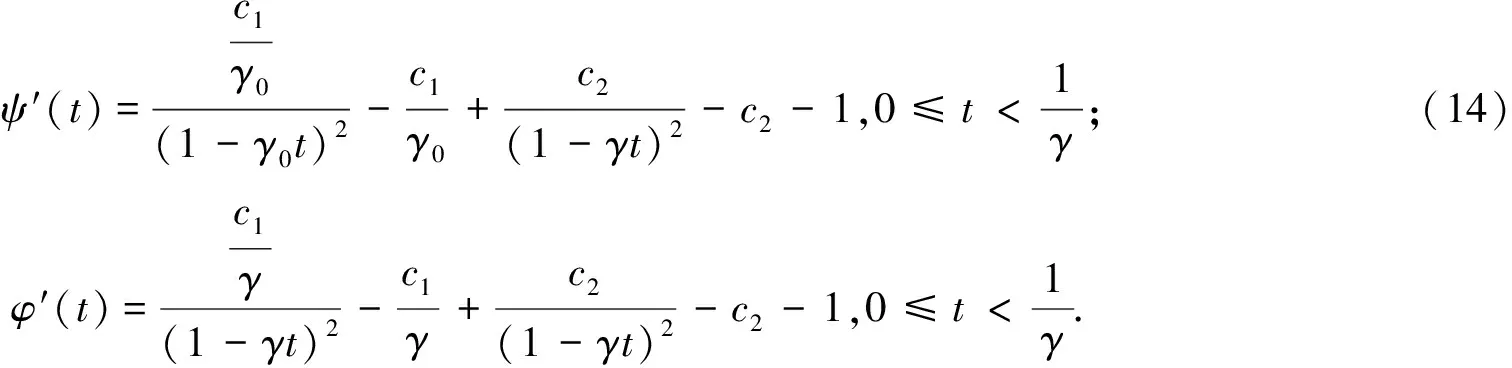
(15)
(16)
令
易知,g′(x)>0,从而g(x)关于x单调递增.由γ0≤γ,有g(γ0)≤g(γ).比较式(14)和式(15),有
ψ′(t)≤φ′(t).
(17)
所以,p*≥r*.引理2证毕.
引理3[1]若
(18)
则函数φ有2个零解
(19)
且满足
λ 引理4若 (20) 成立,则式(10)定义的ψ有2个零解s*和s**,且 λ 由式(20)及引理3知,h(t)=0有2个正解.记较小的正根为h*,则λ 综上,可得λ 下面定义2个序列:令t0=s0=0,{tn}和{sn}由以下迭代产生: (22) 引理5[1]令t*由式(19)所定义,且{tn}由式(21)产生.若式(18)成立,则 tn 引理6假设式(20)成立.令s*是ψ在区间[0,p*]上的零点,且{sn}由式(22)产生,那么 sn (23) 从而{sn}单调递增且收敛于s*. 证明 用数学归纳法证明式(23).当n=0时,s0=0,s1=λ,由引理4知,s0<λ ψ(sn)>0. (24) 由式(17)知,-ψ′(t)≥-φ′(t).又因为φ′严格递增且φ′(r*)=0,所以,由引理4知 -ψ′(sn)≥-φ′(sn)>-φ′(r*)=0. (25) 由式(25)和式(24)可得 因此,式(23)对所有的n≥0成立.这就意味着{sn}单调递增且收敛到一点,设为υ.易知υ∈[0,p*]且υ是函数ψ的一个零点(令式(22)中n→∞).注意到s*是函数ψ在区间[0,p*]上唯一的零点,由此可知υ=s*,所以{sn}单调收敛于s*.引理6证毕. (26) (27) ‖xn+1-xn‖≤sn+1-sn; (28) ‖xn-x*‖≤s*-sn,n=0,1,…. (29) 证明 用数学归纳法证明对所有的k≥0,有 (30) ‖xk+1-xk‖≤sk+1-sk; (31) (32) 由定理1的假设知,式(30)对k=0成立.由算法1知, ‖x1-x0‖≤‖f′(x0)-1f(x0)‖+‖f′(x0)-1r0‖. ‖z-x0‖≤‖z-x1‖+‖x1-x0‖≤s*-s1+s1-s0=s*-s0. 因此,式(31)、式(32)对k=0成立.现假设式(30)~式(32)对所有满足k≤n的正整数k成立,那么 ‖xn+θ(xn+1-xn)-x0‖≤sn+θ(sn+1-sn)≤s*,θ∈(0,1). 由式(9)、式(16)、引理4及引理6有 (33) 令引理1中的x=xn+1,则 (34) 由式(14)得 再根据式(34)有 ‖f′(xn+1)-1f′(x0)‖≤-ψ′(sn+1)-1. (35) 由算法1知 ‖+‖f′(x0)-1rn‖=I1+I2. (36) 接下来分别估计I1和I2.首先,由γ-条件知 因为式(31)、式(32)对所有满足k≤n的正整数k成立,所以 (37) 下面估计I2.因为f ′(x0)-1f ′(xn)=I+f ′(x0)-1(f ′(xn)-f ′(x0)),故由式(7)知 (38) 由算法1有 ‖f′(x0)-1f′(xn)(xn+1-xn)‖≥‖f′(x0)-1f(xn)‖-‖f′(x0)-1rn‖. 因为式(30)对k≤n成立,所以由式(4)得 ‖f′(x0)-1f′(xn)(xn+1-xn)‖≥‖f′(x0)-1f(xn)‖-η‖f′(x0)-1f(xn)‖2≥ 进一步可以得到 (39) 结合式(4)有 注意到sn (40) 根据式(36)、式(37)及式(40)有 结合式(9)、式(10)及式(22)可得 (41) 这就证明了式(30)对所有的k≥0成立. 根据算法1知 ‖xn+2-xn+1‖=‖f ′(xn+1)-1f ′(x0)(-f ′(x0)-1f(xn+1)+f ′(x0)-1rn+1)‖≤ ‖f ′(xn+1)-1f ′(x0)‖(‖f ′(x0)-1f(xn+1)‖+‖f ′(x0)-1rn+1‖)≤ 由式(22)、式(35)及式(41)可得 因此,式(31)对所有的k≥0成立. ‖μ-xn+1‖≤‖μ-xn+2‖+‖xn+2-xn+1‖≤s*-sn+2+sn+2-sn+1=s*-sn+1, 综上,式(30)、式(32)对所有k≥0成立. 因此,y*=x*.定理1证毕. 0≤sn≤tn; 0≤sn+1-sn≤tn+1-tn; 0≤s*-sn≤t*-tn. 注3本文没有给出与文献[12]一致的Smale型收敛准则,要得出相关结论,还需要做进一步的研究. 参考文献: [1]Wang Xinghua.Convergence of Newton′s method and inverse function theorem in Banach space[J].Math Comp,1999,68(225):169-186. [2]王兴华,韩丹夫.点估计中的优序列方法以及Smale定理的条件和结论的最优化[J].中国科学:A 数学,1990,19(9):135-144. [3]Wang Xinghua,Han Danfu.Criterionαand Newton′s method[J].Numer Math Appl,1997,19:96-105. [4]Smale S.Complexity theory and numerical analysis[J].Acta Numer,1997,6(1):523-551. [5]Kantorovich L V.On Newton′s method for functional equations[J].Dokl Akad Nauk,1948,59(7):1237-1240. [6]Smale S.Newton′s method estimates from data at one point[M].New York:Spring-Verlag,1986. [7]Dembo R S,Eisenstant S C,Steihaug T.Inexact Newton methods[J].Numer Anal,1982,19(2):400-408. [8]Argyros I K.Focing sequence and inexact Newton iterates in Banach space[J].Appl Math Lett,2000,13(1):77-80. [9]Ypma J T.Local convergence of inexact Newton methods[J].SIAM Numer Anal,1984,21(3):583-590. [10]Guo Xueping.On semilocal convergence of inexact Newton methods[J].Comput Math,2007,25(2):231-242. [11]白中治,童培莉.不精确Newton法与Broyden法的仿射不变收敛性[J].电子科技大学学报,1994,23(5):535-540. [12] Shen Weiping,Li Chong.Smale′sαtheory for inexact Newton methods under theγcondition[J].Math Anal Appl,2010,369(1):29-32.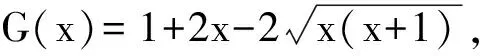

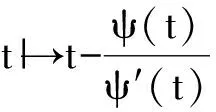
2 收敛性分析