拓扑平带上的分数量子反常霍尔效应(二)*

王一飞， 龚昌德,2

(1.浙江师范大学 海峡两岸统计物理与凝聚态理论研究中心,浙江 金华 321004；2.南京大学 固体微结构国家实验室，江苏 南京 210093)

本文是该综述介绍的第2部分.此前第1部分的主要内容为：领域概况、模型哈密顿量与拓扑平带、玻色子分数量子反常霍尔效应、非阿贝尔型量子反常霍尔效应.第2部分的主要内容为：C=2拓扑平带上的分数量子反常霍尔效应、分数量子反常霍尔态中的边缘激发、总结和展望.

1 C=2拓扑平带上的分数量子反常霍尔效应

传统的朗道能级及最近发现的拓扑平带的陈数都是C=1.而高陈数的能带在晶格体系中是有可能的，进而高陈数的拓扑平带也是可以实现的.由于高陈数的拓扑平带没有连续极限(朗道能级C=1)的对应，其中可能的分数量子反常霍尔效应没有连续模型的直接对应.笔者提出一个C=2的拓扑平带模型，发现了其中1/3 填充的玻色子分数量子反常霍尔效应[1].该奇数分母的分数量子反常霍尔态不是传统的玻色型Laughlin态(其填充数的分母必为偶数)，没有连续极限(朗道能级C=1)的直接对应，也不能用复合费米子图像描述.一种可能的理论描述是具有内秉隐藏结构的“两分量”分数拓扑相，内秉两分量之间由晶格对称性相互耦合，具有隐藏的对称性[2-3].笔者还观察到1/4填充的异常玻色拓扑相(拓扑简并度和量子化陈数的粒子数奇偶效应)、1/5填充的费米子分数量子反常霍尔效应.笔者和同行的系统数值研究[1-2,4]发现,使得高陈数分数拓扑相的研究新领域引起国际同行的迅速关注和研究热情.

1)C=2拓扑平带模型.引入三角晶格上三能带的相互作用硬核玻色子模型

(1)

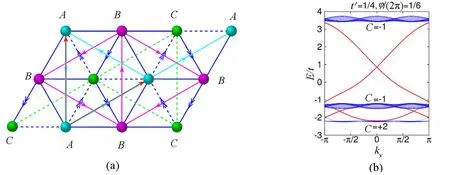
图1 三能带三角晶格模型

图1为三能带三角晶格模型,最近邻(NN)和次近邻(NNN)沿实线(虚线)的跳跃积分为正(负),箭头表示最近邻跳跃中的相位(其符号由箭头方向表示)及次近邻跳跃中的相位,具体见图1(a)；图1(b)为 图1(a)中三角晶格模型的边界态，最低的拓扑平带的陈数为C=+2.

该三角晶格模型有3套子格，即每个元胞中有3个格点，故有3个单粒子能带.此处,笔者采用参数t=1,t′=1/4(跳跃积分符合图1(a)所示)，φ/(2π)=1/6,最低能带的陈数为C=2,平坦率为15的拓扑能带,具体见图1(b).

2)最低能谱和能隙.考虑了多个晶格尺寸，Ns=36(3×3×4)，45(3×3×5)，54(3×3×6)和63(3×3×7),在相互作用为V1=V2=0.0附近υ=1/3填充的最低能谱处，发现了υ=1/3玻色分数量子反常霍尔态的特征：三重准简并的基态组(E3-E1～0)，且与高能激发态之间有较大特征能隙E4-E3≫E3-E1,见图2(a).

类似于C=1拓扑平带上的分数量子反常霍尔态[5-7]，若(k1,k2)是准简并基态组中的一个基态的动量分区，则可以在动量分区(k1+Nb,k2+Nb)[mod(N1,N2)]中发现另一个基态，阐明该体系中特征的动量空间对称性.对于Ns=36,45,63这3种格子，3个基态都分别处于(0,0),(1,0),(2,0)动量分区；而对于Ns=54格子，由于Nb/N1和Nb/N2都是整数，所有3个(能量非常接近的)基态都处于(0,0)动量分区.

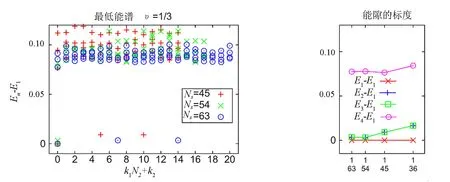
(a) 低能谱En-E1随动量k1N2+k2的变化，3个格子尺寸NS=45,54,63，填充数υ=1/3，V1=V2=0.0 (b)能隙随4个格子尺寸1/Ns的变化

3)Berry曲率和多体陈数.对于1/3填充的玻色子分数量子反常霍尔态，当调节边界相位角时，基态组保持其准简并性且与低能激发态之间保持较大能隙，表明该拓扑相的稳定性.对于Ns=45格子，其3个基态分别处于(0,0),(1,0)及(2,0)动量分区，3个动量分区的Berry曲率(边界相位空间分为10×10网格)求和给出总的Berry相位为4π(每个基态几乎精确贡献了(4π)/3的Berry相位，精度达10-6)，因此,整个基态组的总陈数为Ctot=2，则每个基态的分数化霍尔电导为2e2/(3h).

4)准空穴分数统计.为了探讨该1/3玻色子分数量子反常霍尔态的分数统计，笔者考虑在υ=1/3填充的情况下移去一个玻色子来看其准空穴激发谱.例如图3(a)中，Ns=45和Nb=4 的情形，准空穴激发谱显示出和高能激发态之间的特征能隙，在特征能隙之下的每个动量分区中有5个低能准空穴态，总计75个低能准空穴激发态.这个数目和将1个空穴分为3个准空穴(每个携带分数电荷1/3)的计数规则是一致的，即符合Laughlin1/3费米子分数量子霍尔态的广义Pauli不相容原理[7].

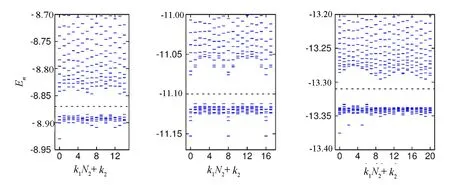
(a)Ns=45，Nb=4 (b)Ns=54，Nb=5 (c)Ns=63，Nb=6

5)1/5费米分数量子反常霍尔效应.对于陈数C=2这样的拓扑平带上相互作用的无自旋费米子(哈密顿量中的玻色算符替换为费米算符)，笔者也观察到υ=1/5填充的分数量子反常霍尔效应[8].计算了4个普通晶格尺寸Ns=45(3×5×3),60(3×5×4),75(3×5×5)和90(3×5×6).将费米子数记为Nf，拓扑平带的费米填充数为υ=Nf/Norb.与V1=V2=0.0处υ=1/3的玻色分数量子反常霍尔态不同， υ=1/5填充的费米分数量子霍尔反常态需要非零的短程排斥相互作用(V1,V2及第3近邻相互作用V3).这一点类似于C=1拓扑平带上的1/5费米分数量子反常霍尔态[5]或1/4玻色分数量子反常霍尔态[6].对于υ=1/5，基态拓扑简并度为d=5.对于Ns=45,60,90格子，基态组中的5个基态分布在不同动量分区，比如Ns=45格子的(0,0),(1,0),(2,0),(3,0),(4,0)动量分区；而对于Ns=75格子，Nf/N1和Nf/N2皆为整数，所有5个基态都在同一个(0,0)动量分区，具体见图4,基态组中准简并度已在图4中标出.

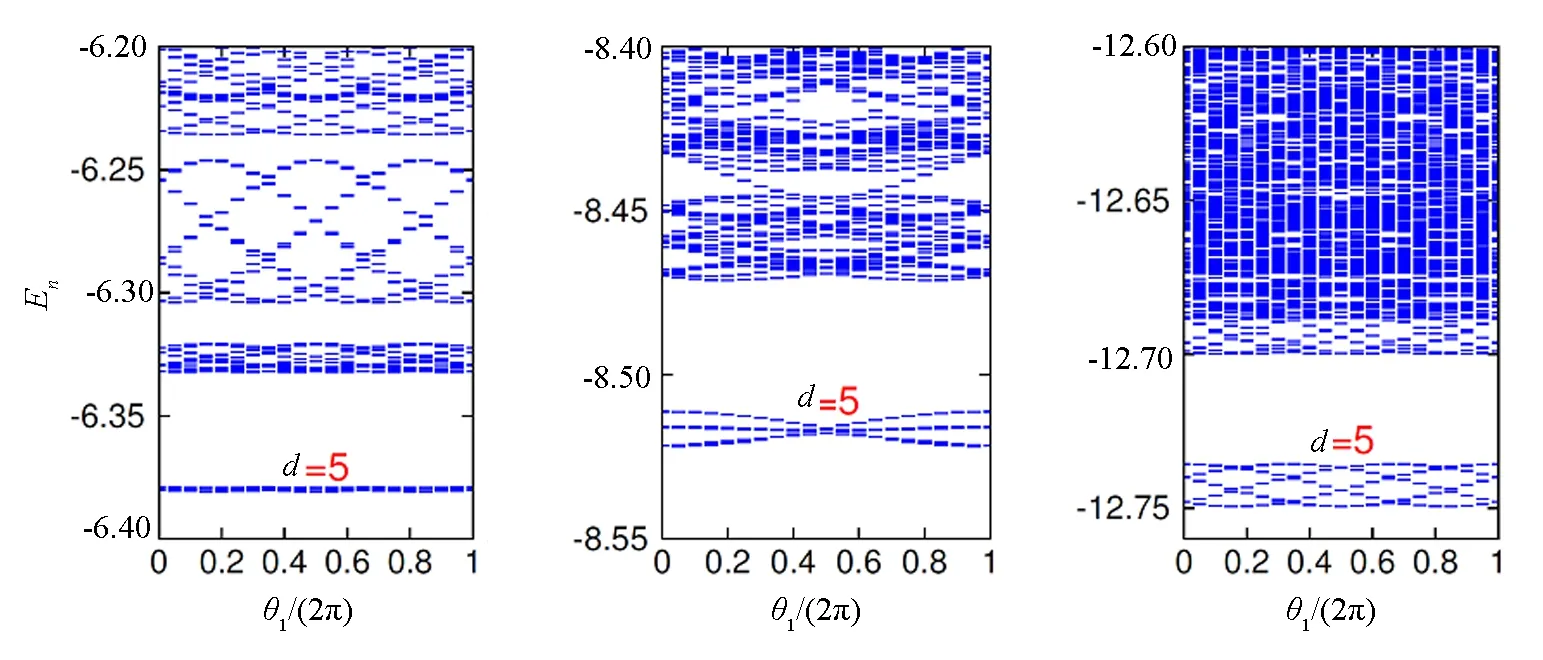
(a)Ns=45,Nf=3 (b)Ns=60,Nf=4 (c)Ns=90,Nf=6

2 分数量子反常霍尔态中的边缘激发

尽管此前的研究已经牢固地确定了分数量子反常霍尔态(FCI/FQAH)的各种拓扑性质，但是边缘激发的研究在原则上可以提供另一个揭示体态拓扑序的窗口[9].考虑到将来可能会首先在光晶格冷原子体系实现分数量子反常霍尔态(FCI/FQAH)[10]，边缘激发也可以提供一个可行的实验探测手段.最近，本课题的实空间严格对角化(ED)计算发现了碟形几何结构上的边缘激发谱[8]，而同行基于量子纠缠谱的研究[11]也给出了类似结果.笔者考虑了硬核玻色子填充到Haldane碟形模型和Kagome格子碟形模型中，发现了一系列特征边缘激发谱，符合手征Luttinger液体理论[11].通过在碟形结构中心插入磁通并调节，进一步检验了这些激发态的可压缩性确实是载流的手征边缘态.

2个格子的碟形几何结构如图5所示，显示出C6旋转对称性.在该有限尺寸系统中，需要一个额外的势阱来约束FCI/FQAH液滴，而在FCI/FQAH液滴的边缘可以有边缘激发模式围绕碟形结构传播.此处选取通常的谐振子势阱V=Vtrap∑r|r|2nr.其中:Vtrap为势场强度(以最近邻跳跃积分为能量单位);|r|为格点到碟形结构中心的半径(以半个晶格常数a/2为长度单位);nr是玻色子粒子数算符.

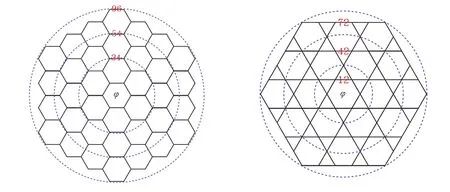
(a)碟形蜂窝格子 (b)碟形Kagome格子

首先考虑蜂窝格子碟形模型，在较大的势阱强度Vtrap范围及各种蜂窝格子碟形结构尺寸Ns=24,54,96上，都观测到了明显的特征边缘激发谱.这里给出另一个格子，即Kagome格子碟形模型上的更加显著的边缘激发谱.笔者研究了Ns=12,30,42,72等不同尺寸的Kagome格子碟形结构,由于该系统具有C6旋转对称性，每个能量本征态可以用角动量量子数L=0,1,2,3,…,(mod) 6来划分.图5中显示了N2=72格点的Kagome格子碟形结构上的典型边缘激发谱.每个角动量分区中有1个或几个准简并的低能本征态且与高能激发态之间有较大特征能隙.结果将显示每个角动量分区的低能本征态计数符合分数量子霍尔效应的边缘激发理论，即手征Luttinger液体理论.

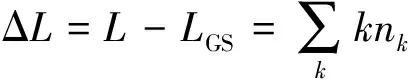
根据流体动力学方法[9]，υ=1/m填充的Laughlin态的FQHE液滴的低能边缘激发由Kac-Moody代数给出，形成手征Luttinger液体，其有效哈密顿量为

(2)

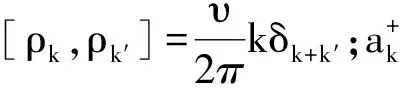
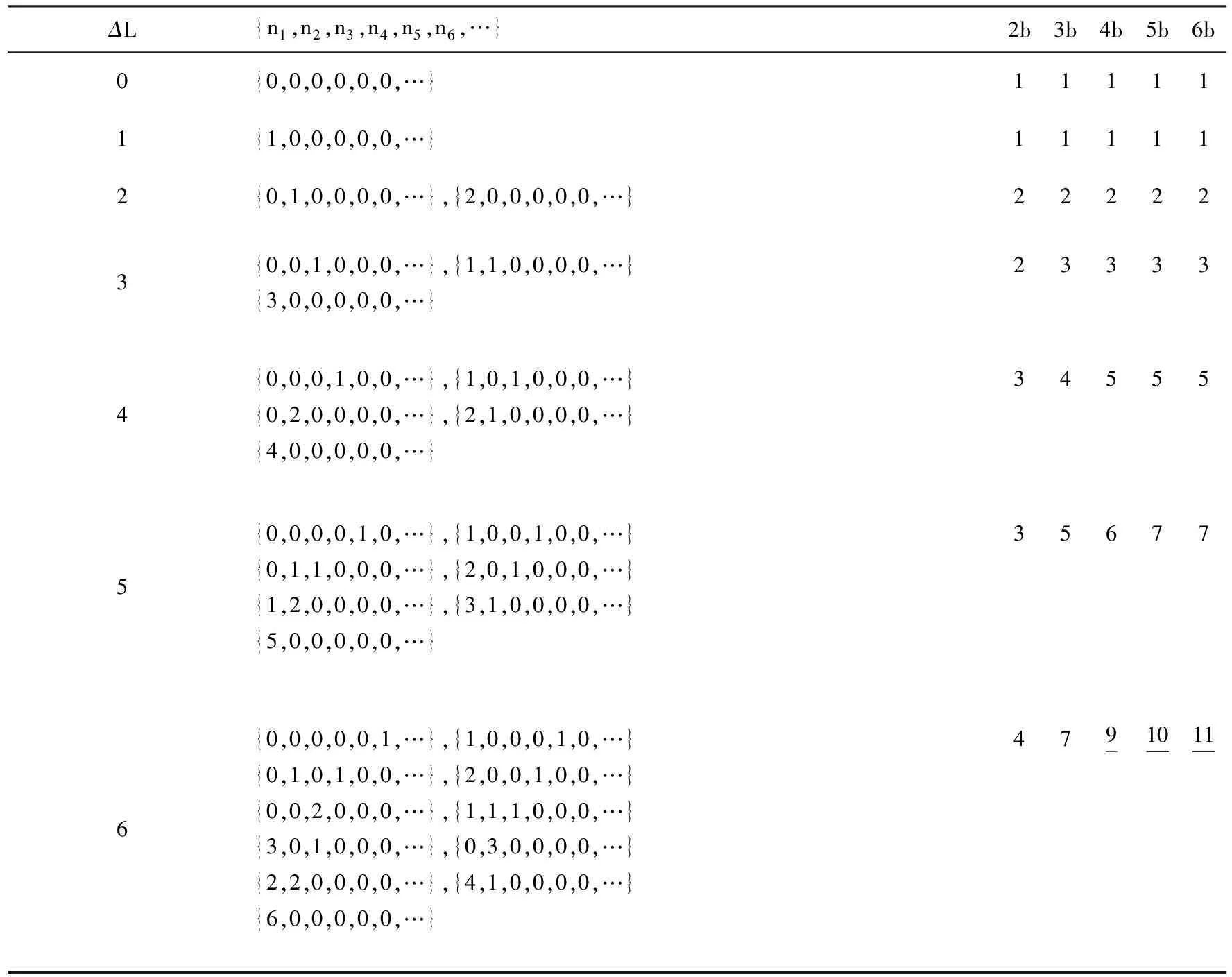
表1 k=1,2,3,4,5,6,…轨道上的手征边缘玻色子的占据分布

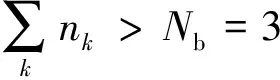
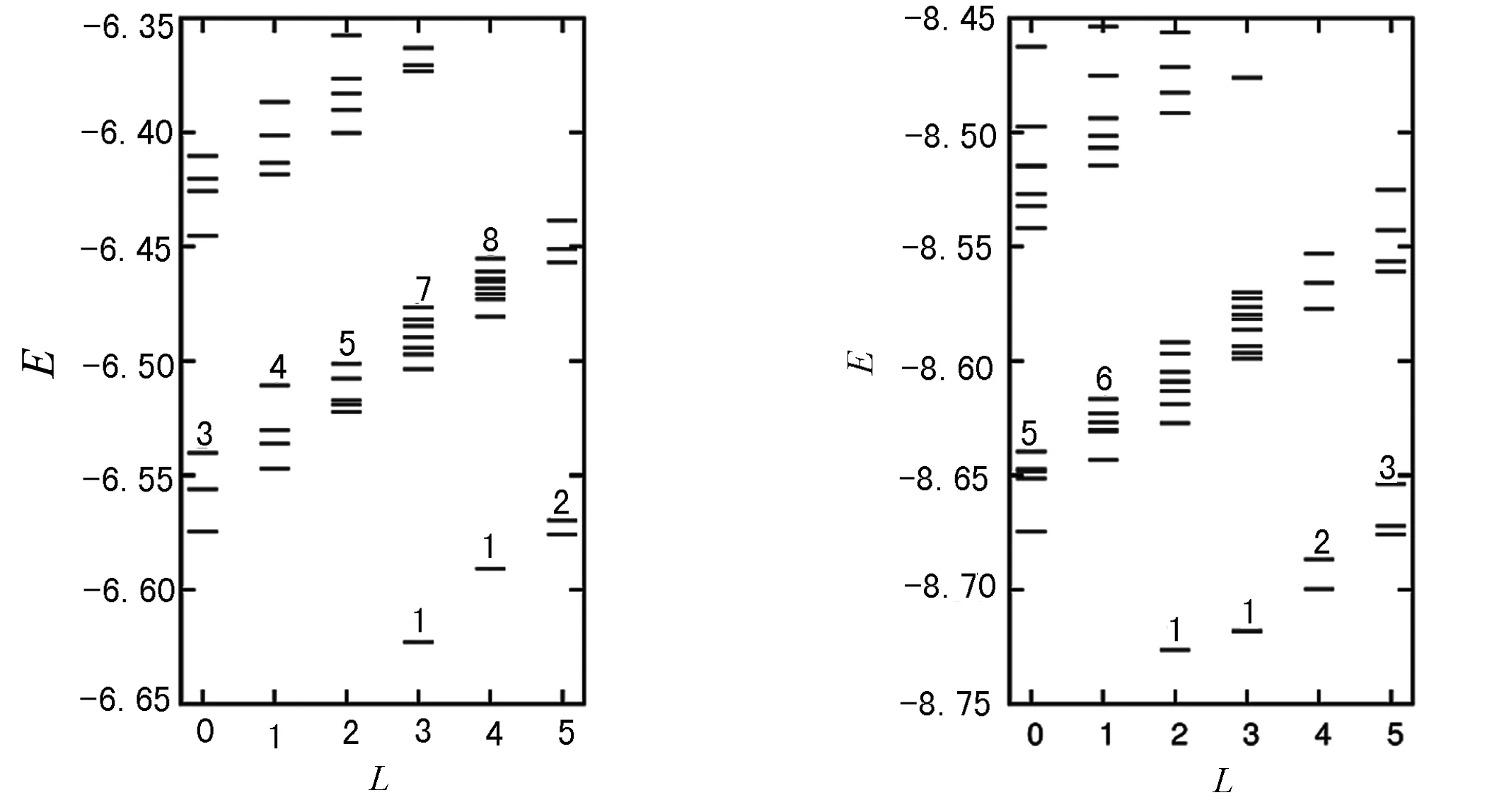
(a)Nb=3 (b)Nb=4

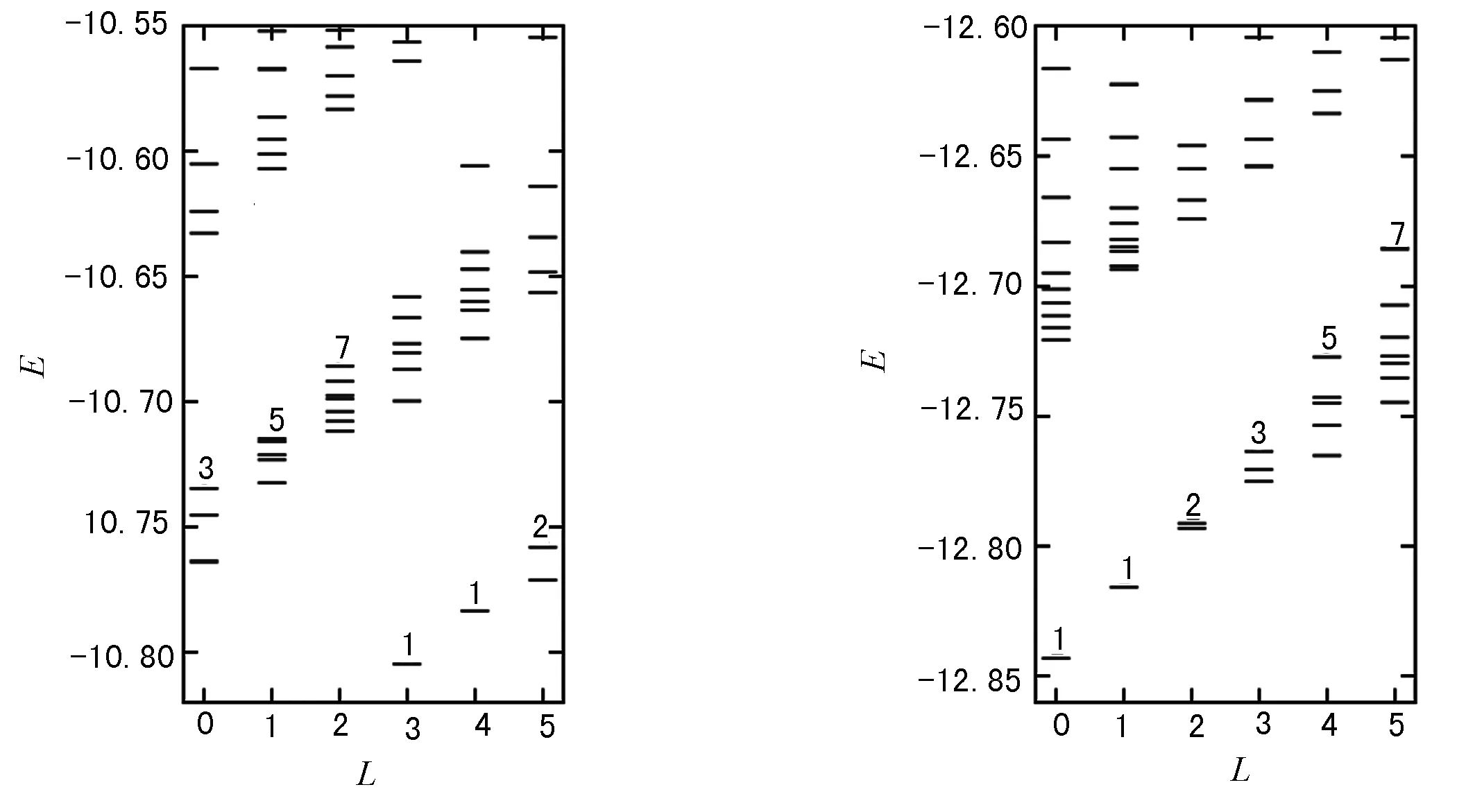
(c)Nb=5 (d)Nb=6

3 总结和展望

拓扑平带上发现了一类新奇的分数量子霍尔效应，系统的数值研究提供了如下证据：拓扑准简并的基态组，拓扑稳定的特征能隙，基态组的特征动量关联，基态组的拓扑演化，光滑的Berry曲率，分数化霍尔电导(或称分数化陈数)，准空穴激发的分数电荷统计，手征边缘激发.该效应不同于传统朗道能级上的连续型分数量子霍尔效应，无须外加强磁场，有较大特征能隙，可在较高温度下存在，无需单粒子朗道能级，不能用常规Laughlin波函数描述.这些无外加磁场、无朗道能级的分数化现象，定义了一类新的分数拓扑相，也称为分数陈绝缘体，其中的分数量子霍尔效应也称为分数量子反常霍尔效应.

对于新开辟的拓扑平带领域，可以进一步提出以下几个的问题：1)已经发现的拓扑平带上的分数量子反常霍尔态都有连续极限下(即朗道能级)的直接或间接对应.在拓扑平带上有没有全新的分数化的拓扑序，完全没有连续极限的对应？常规拓扑相的边缘态与体态之间有对应关系，那么拓扑平带上的分数拓扑相有无异常的边缘激发？2)连续朗道能级的陈数为1，而晶格模型中的拓扑能带的陈数在原理上可以有较高的数值.强关联相互作用玻色子或费米子分数填充高陈数的拓扑平带，有无奇异的分数统计？有无异常的边缘激发？有无全新的非阿贝尔型分数统计？3)对于朗道能级上的分数量子霍尔效应，复合费米子图像简洁而深刻.那么对于拓扑平带中的分数量子霍尔效应，复合费米子图像是否正确？如何构建合理的解析波函数？4)对于分数填充、有吸引相互作用的情形，是否可能发现新的异常拓扑相，既具有分数化的特征，也具有超导配对关联的特征？分数化的超导相、超流相是否可能存在？

考虑到该领域的最新进展，一些可能的理论研究方向如下：提出其他拓扑平带模型，包括更好的高陈数拓扑平带模型，同时具有多个拓扑平带的晶格模型；研究拓扑平带上分数拓扑相的异常边缘激发；研究拓扑平带上的阿贝尔型分数统计、非阿贝尔型分数统计；研究高陈数拓扑平带上的奇异分数统计和边缘激发；探索可能的分数化超导相、超流相；将拓扑平带上分数量子霍尔效应的数值波函数与解析波函数做定性、定量的比较研究；探索拓扑序之间,拓扑序与超流体相、固体相、超固体相之间拓扑量子相变的特征.而该领域的实验研究更加迫切：如何在凝聚态材料中实现拓扑平带？如何在冷原子光晶格中实现拓扑平带？如何实现这两类体系中的分数量子反常霍尔态？如何探测其中的拓扑序？如何探测其中的分数化？

致谢

在此感谢我们的合作者：加州州立大学北岭分校的盛冬宁教授、清华大学高等研究院的姚宏研究员、加州大学圣巴巴拉分校Kavli理论物理研究所的顾正澄博士，以及研究生陈文潮、刘晓萍、骆炜炜同学.

参考文献：

[1]Wang Yifei,Yao Hong,Gong Changde,et al.Fractional quantum Hall effect in topological flat bands with Chern number two[J].Phys Rev B,2012,86(20):201101.

[2]Sterdyniak A,Repellin C,Bernevig B A,et a l.Series of Abelian and non-Abelian states inC>1 fractional Chern insulators[J].Phys Rev B,2013,87(20):205137.

[3] Barkeshli M,Qi Xiaoliang.Topological nematic states and non-Abelian lattice dislocations[J].Phys Rev X,2012,2(3):031013.

[4] Liu Zhao,Bergholtz E J,Fan Heng,et al.Fractional Chern insulators in topological flat bands with higher Chern number[J].Phys Rev Lett,2012,109(18):186805.

[5]Sheng D N,Gu Zhengcheng,Sun Kai,et al.Fractional quantum Hall effect in the absence of Landau levels[J].Nature Commun,2011,2:389

[6]Wang Yifei,Gu Zhengcheng,Gong Changde,et al.Fractional quantum Hall effect of hard-core Bosons in topological flat bands[J].Phys Rev Lett,2011,107(14):146803.

[7]Regnault N,Bernevig B A.Fractional Chern insulator[J].Phys Rev X,2011,1(2):021014.

[8]Luo Weiwei,Chen Wenchao,Wang Yifei,et al.Edge excitations in fractional Chern insulators[J].Phy Rev B,2013,88(16):161109.

[9]Wen Xiaogang.Topological orders and edge excitations in fractional quantum Hall states[J].Adv Phys,1995,44(5):405-473.

[10] Yao N Y,Laumann C R,Gorshkov A V,et al.Topological flat bands from dipolar spin systems[J].Phys Rev Lett,2012,109(26):266804.

[11]Liu Zhao,Kovrizhin D L,Bergholtz E J.Bulk-edge correspondence in fractional Chern insulators[J].Phy Rev B,2013,88(8):081106.