拉伸应力作用下共轭高分子的能带结构研究*

童国平， 林 征， 陈 琼， 沈晓萍， 李 盛

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

0 引 言

聚乙炔是一种结构最简单的导电高分子聚合物[1].纯净的聚乙炔虽有可移动的π电子,但不导电，这是由于维度性之故[2].后来,人们发现可以通过掺杂来调控其导电性质，即从绝缘体到良导体的转变[3].另一方面，反式聚乙炔存在A相和B相，而这两相的能量相等，因此，能量是简并的.如果纯净的反式聚乙炔要导电的话，是在A相和B相之间形成带电扭结孤子[4]，这种孤子的运动就形成了电流，这一非线性元激发的理论得到了实验的证实[5].由于反式聚乙炔是半满能带的准一维晶格，原子等距离排列是不稳定的，碳原子要发生偏移(二聚化)，成为单双键交替排列的分子链.二聚化使聚乙炔在费米面处产生一个能隙，使电子占据态的能量降低.近些年来，人们把目光转向双极化子与激子之间的散射[6]、发光二极管[7-8]、横向取代反式聚乙炔的低激发态[9]等的研究.

在这项工作中，笔者将在改进的SSH(Su-Schrieffer-Heeger)模型[10]基础上考虑至三近邻相互作用，并利用弹性形变理论研究反式聚乙炔的能带结构随应力变化规律，其目的是寻找另一种调控聚乙炔导电能力的有效途径.笔者将在链的方向上施加一小小的单轴应力，使其跳跃能发生改变，从而导致能带结构发生变化.通过计算表明，这一方法能够有效改变聚乙炔的导电性.因此，研究这种聚乙炔的形变是有意义的.

1 理论方法

在修正的SSH模型中，聚乙炔中电子的哈密顿量、包括非近邻电子间的跳跃可表示为

(1)

式(1)中：an,s是第n个格点上自旋为s的电子的湮灭算符；ε0是格点的自由能；数值tn+1,n，tn+2,n和tn+3,n分别代表最近邻、次近邻和第3近邻的电子跳跃能.

通过傅里叶变换

(2)

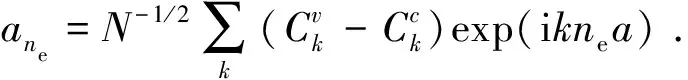
(3)

下标no和ne分别表示晶格的奇偶数.再通过正交变换

(4)

(5)

可得哈密顿量H的对角化形式为

(8)

式(7)～式(8)中，t3是次近邻电子跳跃能，与二聚链的二聚化程度有关，其中:

(9)

εk=-(t1+t2)cos(ka)-(t4+t5)cos(3ka);

(10)

Δk=(t1-t2)sin(ka)+(t4-t5)sin(3ka).

(11)

导带底与价带顶的能量差即为能隙

(12)

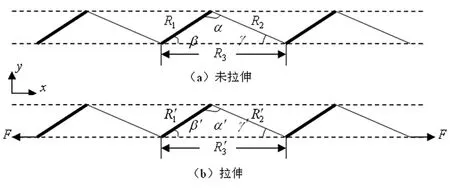
图1 反式聚乙炔链的拉伸作用

在不受力情况下，聚乙炔在二聚化过程中形成了单双键交替的高分子链结构，如图1(a)所示.其中:R1是聚乙炔分子链结构中双键(粗线)的长度;R2是单健(细线)的长度;R3是晶格结构中第n个碳原子与第n+2个碳原子间的距离;α表示键角，并设该键角不变(120°);β是短键与x轴的夹角;γ是长键与x轴的夹角.在受力应变下，聚乙炔分子结构中的键长发生变化，受力沿x轴方向，如图1(b)所示.

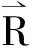
(13)

式(13)中：ε是沿x轴的应力作用下键长的相对变化量;ε=1%对应的单轴应力为10GPa.由几何关系，并结合式(13)，可得到下列表达式:

(16)

R3=R1cosβ+R2cosγ.

(17)

在实际情况中，聚乙炔在受力应变时由于边缘驰豫效应，分子链两端的形变会比里面的形变稍大些，而笔者认为这里讨论的时候，本身这种受力作用下的形变量就很小，忽略了边缘效应产生的影响，近似认为形变后聚乙炔分子仍呈有规则的几何结构.

应变前后电子Hopping能量与键长的关系可由哈里森公式[12]得到,

(18)

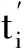
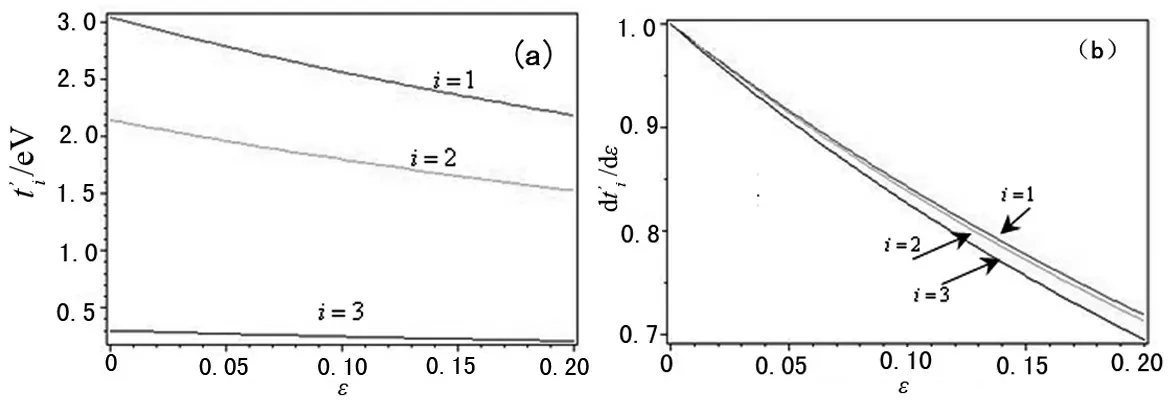
图2 电子跳跃能及其变化率与应力的关系

2 结果与讨论

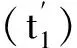
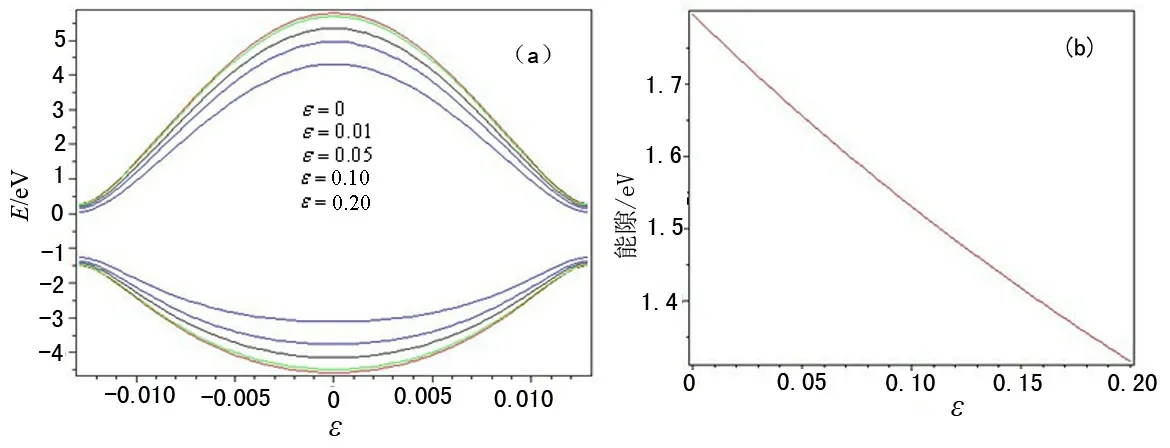
图3 反式聚乙炔的能带结构与能隙随拉伸应力的变化

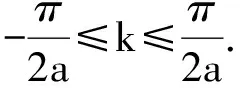
3 结 论

反式聚乙炔受力应变后，其键长变大，相应的电子跳跃能减小.当应变较小时，键长的变化近似为线性关系，相应的电子跳跃能也呈现近似的线性关系.随着应力的增加，能带宽度和能隙都有明显变窄，但能带宽度的变化要比能隙的变化来得明显一些.拉伸应力能够调节电子的局域性与扩展性，但其局域性的调控幅度要大于其扩展性的幅度.因而，通过拉伸形变可以调控聚乙炔的能带结构，但其幅度有限.

笔者的计算中没有考虑电子-电子相互作用，也没有考虑拉伸应力下的不等性sp2杂化问题.这些都是有趣的问题，有待进一步深入研究.

参考文献：

[1]Shirakawa H,Ito T,Ikeda S.Raman scattering and electronic spectra of poly(acetylene)[J].Polymer Journal,1973,4(4):460-462.

[2]孙鑫.高聚物中的孤子和极化子[M].成都：四川教育出版社，1987.

[3]Feldblum A,Kaufman J H,Etemad S,et al.Opto-electrochemical spectroscopy of trans-(CH)x[J].Phys Rev B,1982,26(2):815-826.

[4]Su W P,Schrieffer J R.Fractionally charged excitations in charge-density-wave systems with commensurability[J].Phys Rev Lett,1981,46(11):738-741.

[5]Heeger A J,Kivelson S,Schrieffer J R,et al.Solitons in conducting polymers[J].Rev Mod Phys,1988,60(3):781-850.

[6]Sun Z,Li Y,Xie S J,et al.Scattering processes between bipolaron and exciton in conjugated polymers[J].Phys Rev B,2009,79(20):201310.

[7]Li Sheng,Tong Guoping,George T F.Electroluminescence enhancement in polymer light-emitting diodes through hole injection layer insertion[J].J Appl Phys,2009,106(7):074513.

[8]Li Sheng,Tong Guoping,George T F.Radiative decay of singlet excitons and carrier-fusion-induced electroluminescence enhancement of polymer light-emitting diodes[J].J Phys Chem B,2009,113(46):15231-15236.

[9]Kumar M,Ramasesha1 S.Low-lying states of transverse substituted trans-polyacetylene and trans-polyacetylene:A comparative DMRG study[J].Phys Rev B,2010,81(3):035115.

[10]Su W P,Schrieffer J R,Heeger A J.Solitons in polyacetylene[J].Phys Rev Lett,1979,42(25):1698-1701.

[11]Tong Guoping,Feng Jiaxian,Li Henian.Non-nearest-neighbor hopping in polyacetylene[J].Acta Physica Sinica,1995,4(4):278-290.

[12]Harrison W A.Electronic structure and the properties of solids[M].San Francisco：Freeman，1980.