Dirichlet空间上Toeplitz乘积的有界性*

于 涛, 陆俏飞

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

0 引 言

本文中，令D是复平面C中的开单位圆盘，dA表示D上的正规化面积测度.把所有满足下式的D上函数u构成的空间称为Sobolev空间:

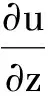
〉L2.

其中,符号〈5,5〉L2表示Lebesque空间L2(D,dA)上的内积.称由Sobolev空间W1,2(D)中所有在原点处为0的解析函数构成的子空间为Dirichlet空间，记为D,它是一个具有如下内积的Hilbert空间:

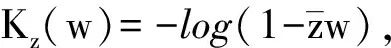
f(z)=〈f,Kz〉.

(1)

(2)

Sarason在文献[1]中同时提出了Bergman空间上的类似问题;文献[4]给出与Hardy空间情形类似的回答，此时条件(1)和条件(2)中的Piosson扩张改为Bergman空间上的Berezin变换;文献[5-6]分别将该结果推广到单位圆盘和单位球上的加权Bergman空间;文献[7-9]分别将该结果推广到多圆盘和单位球上的Bergman空间.本文的目的是在Dirichlet空间上考虑Toeplitz乘积有界性的条件.

Sobolev空间W1,∞(D)定义为

其中,L∞(D)是D上所有本质有界可测函数构成的空间.空间W1,∞(D)的范数定义为

令P为由W1,2(D)到D上的正交投影，则P是可表示为如下的积分算子:

(3)

给定u∈W1,∞(D)，定义D上以u为符号的Toeplitz算子Tu为

Tuf=P(uf).

(4)

容易看出,对于每个u∈W1,∞(D),Toeplitz算子 Tu是有界的.

Dirichlet空间上Toeplitz算子已被广泛研究.例如:文献[10]研究了具有连续可导符号Toeplitz算子的Fredholm性质;文献[11]研究了当符号函数是调和函数时，Toeplitz算子的交换性和正规性等;文献[12]研究了W1,∞(D)符号Toeplitz算子的交换性、乘积和模有限秩交换等代数性质.

对于u∈W1,2(D)，式(4)的右边对于 f∈D ∩W1,∞(D)还是有意义的，此时Toeplitz算子Tu可以看作D上的稠定义算子.若再设v∈W1,2(D)，按照式(3)和式(4),对于 f∈D ∩W1,∞(D),

上述积分是可积的.因此,可将TvTu看作从D到H(D)(D上所有解析函数的空间)的稠定义算子.

本文的主要结果是Toeplitz乘积在 D上有界的一个充分条件和一个必要条件.

定理1设 f,g∈D，如果存在ε>0，使得

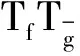
1 预备知识

(5)

(6)

对于w∈D，定义W1,2(D)上的算子Uw为Uwf=f(w)- f ∘ φw.易见算子Uw是D上的自伴酉算子.特别地，当φ∈W1,∞(D)解析时，有

UwTφUw=Tφ ∘ φw+Uw(φ)⊗Kw;

(7)

当 φ∈W1,∞(D)共轭解析时，有

UwTφUw=Tφ ∘ φw.

(8)

关于Uw的定义、式(4)及式(5)可参阅文献[13].

对于 f,g∈D,定义 D上一秩算子 f⊗g为(f⊗g)h=〈 h,g 〉 f,h ∈D.如果T和S是有界线性算子，那么T( f⊗g)S*=(T f)⊗(Sg).

对于w ∈D，令τw表示函数Uw(z)=w-φw，其中z表示D上的恒等映射.

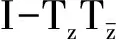
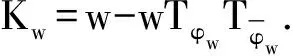
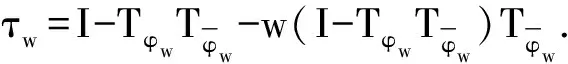
证明 对于w∈D，应用引理1和引理2 及式(7)、式(8)可得

引理3证毕.

证明 令u∈D，v∈D，对于w∈D，有

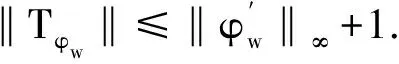
引理5令 f，g∈D，对于w∈D，有

其中,‖5‖H2表示Hardy空间 H2的范数.

证明 令 f∈D，w∈D,则

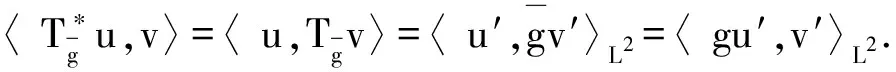
(9)

式(9)中的最后一个等式通过式(5)和式(6)获得.

引理6[13]如果F∈D,G∈D，那么

2 主要结果的证明

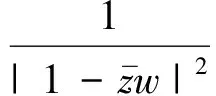
下面对Toeplitz算子作一些估计，这些估计将用于Toeplitz乘积有界性的充分性的证明.

引理7对给定的ε>0，令δ=(2+ε)/(1+ε)，则

1)令g∈D，u∈D，对任意的w∈D，有

2)令 f∈D，v∈D，对任意的 w∈D，有

证明 1)若g∈D,u∈D，则对任意的w∈D，有

因此,

从而

应用Hölder′s不等式，可得

2)令f∈D，v∈D，对任意的w∈D，有

所以

与1)的证明类似，有

引理7证毕.

其中:

由引理 7可得

[P0(|u′|δ)(w)]1/δ[P0(|v′|δ)(w)]1/δdA(w)≤

因为 2/δ>1,从而P0是L2/δ-有界的，所以存在常数C>0,使得

由Cauchy-Schwarz不等式可得

因此,得到关于I1的如下估计:存在常数C>0,使得

完全类似地，可以对I2和I3作出估计.通过对I1，I2和I3的估计，得到存在某个常数M>0，使得

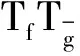
定理2的证明 由引理3，有

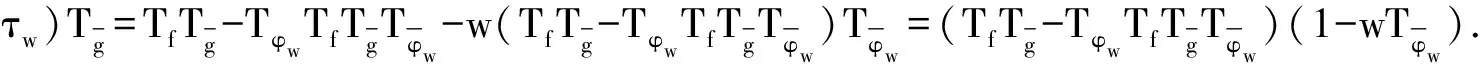
由引理4和引理5可以得到

所以

从而得到定理2的结论.定理2证毕.

参考文献：

[1]Sarason D.Products of Toeplitz operators[C]//Khavin V P,Nikol′skiN K.Linear and complex analysis problem book 3.New York:Springer-Verlag,1994:318-319.

[2]Cruz-Uribe D.The invertibility of the product of unbounded Toeplitz operators[J].Integral Equations Operator Theory,1994,20(2):231-237.

[3]Zheng Dechao.The distribution function inequality and products of Toeplitz operators and Hankel operators[J].J Funct Anal,1996,138(2):477-501.

[4]Stroethoff K,Zheng Dechao.Product of Hankel and Toeplitz operator on the Bergman space[J].J Funct Anal,1999,169(1):289-313.

[5]Stroethoff K,Zheng Dechao.Bounded Toeplitz products on weighted Bergman spaces[J].J Oper Theory,2008,59(2):277-308.

[6]Stroethoff K,Zheng Dechao.Bounded Toeplitz products on Bergman spaces of the unit ball[J].J Math Anal Appl,2007,325(1):114-129.

[7]Stroethoff K,Zheng Dechao.Bounded Toeplitz products on the Bergman space of the polydisk[J].J Math Anal Appl,2003,278(1):125-135.

[8]Park J D.Bounded Toeplitz products on the Bergman space of the unit ball in Cn[J].Integral Equations Operator Theory,2006,54(4):571-584.

[9]Lu Yufeng,Liu Chaomei.Toeplitz and Hankel products on Bergman spaces of the unit ball[J].Chin Ann Math Ser B,2009,30B(3):293-310.

[10]Cao Guangfu.Fredholm properties of Toeplitz operators on Dirichlet space[J].Pacific J Math,1999,188(2):209-224.

[11]Lee Y J.Algebraic propertise of Toeplitz operators on the Dirichlet space[J].J Math Anal Appl,2007,329(2):1361-1329.

[12]Yu Tao.Toeplitz operators on the Dirichlet space[J].Integral Equations Operator Theory，2010,67(2):163-170.

[13]Yu Tao.Operators on the orthogonal complement of the Dirichlet space[J].J Math Anal Appl,2009,357(1):300-306.

[14]Axler S.Bergman spaces and their operators[C]//Conway J B,Morrel B B.Surveys of some recent results in operator theory.New York:Wiley,1988:1-50.