求解无约束优化问题的改进布谷鸟搜索算法

苏芙华，刘云连，伍铁斌

(1. 湖南人文科技学院 a. 物理与电子信息系；b. 机电工程系，湖南 娄底 41 7000；2. 湖南科技大学信息与电气工程学院，湖南 湘潭 41 1201)

求解无约束优化问题的改进布谷鸟搜索算法

苏芙华1a，刘云连1b,2，伍铁斌1b

(1. 湖南人文科技学院 a. 物理与电子信息系；b. 机电工程系，湖南 娄底 41 7000；2. 湖南科技大学信息与电气工程学院，湖南 湘潭 41 1201)

布谷鸟搜索算法是一种基于种群迭代搜索的全局优化算法。为求解无约束优化问题，提出一种改进的布谷鸟搜索算法。利用混沌序列构造初始种群以增加群体的多样性，引入动态随机局部搜索技术对当前最优解进行局部搜索，以加快算法的收敛速度。对4个标准测试函数进行仿真实验，并与其他6种算法进行比较，结果表明，该算法具有较强的全局搜索能力和较快的收敛速度。

布谷鸟搜索算法；无约束优化问题；混沌；动态随机局部搜索；惯性权重；多样性

1 概述

布谷鸟搜索(Cuckoo Search, CS)算法是一种模拟布谷鸟寻窝产卵行为的全局搜索算法[1]。CS算法具有概念简单、参数设置少、容易实现的特点，已被证明在收敛速度和稳定性方面均超过了遗传算法(Genetic Algorithm, GA)和粒子群优化(Particle Swarm Optimization, PSO)算法。因此，CS算法在函数优化、组合优化、神经网络训练、结构优化和多目标优化等领域有着广泛的应用。文献[2]将CS算法应用到13个结构设计优化问题中取得了较好的结果。文献[3]提出一种多目标布谷鸟搜索算法应用于设计优化。文献[4]将CS算法应用到柔性制造系统的调度中。文献[5]将布谷鸟搜索算法应用于图形分割中。

然而，与其他基于种群迭代搜索的全局优化算法一样，CS算法同样存在后期收敛速度慢、局部搜索能力弱和易早熟收敛等缺点。产生早熟收敛等缺陷的根本原因是随着迭代次数的增加种群多样性快速下降。针对以上缺点，文献[6]提出一种基于正交学习方法的改进CS算法，用于求解混沌系统参数优化问题。文献[7]提出一种基于高斯分布的改进CS算法，用于求解无约束优化问题。文献[8]提出一种基于共轭梯度的改进布谷鸟搜索算法，用于求解高维无约束优化问题。文献[9]指出，多样性高的初始种群对寻找全局最优解很有帮助。

为了改善CS算法的性能，本文提出一种求解无约束优化问题的改进CS算法。该算法首先利用混沌序列产生初始种群以维持群体的多样性；在Lévy f light随机搜索中引入惯性权重以增强其全局搜索能力；利用动态随机局部搜索技术对当前最优解进行局部搜索，以加快算法的收敛速度。

2 布谷鸟搜索算法

CS算法模拟了布谷鸟为寻找适合产卵的鸟窝而随机游走的寻窝过程。为了模拟布谷鸟寻窝的行为，需设定以下3个理想的状态[1]：(1)布谷鸟一次只产一个卵，并随机选择鸟窝位置来孵化它。(2)在随机选择的一组鸟窝中，最好位置的鸟窝将会保留到下一代。(3)可利用的鸟窝数量N是固定的，一个鸟窝主人能发现一个外来鸟蛋的概率为Pa。

在CS算法中，一个鸟巢的卵表示一个候选解，一个布谷鸟的卵表示一个新的解。在上述3个理想状态的基础上，布谷鸟寻窝的路径和位置更新公式如下：

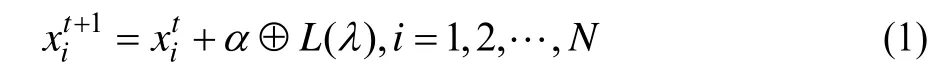
通过位置更新后，用随机数r∈[0,1]与鸟窝的主人发现外来鸟的概率Pa作对比，若r＞Pa，则对xti进行随机改变，否则不变。

CS算法的步骤如下：

Step1设置算法基本参数，在问题的搜索空间中随机产生N个初始鸟窝位置。

Step2计算各鸟窝位置的适应度值，确定当前最佳适应度值及最佳鸟窝位置。

Step3利用式(1)和式(2)对鸟窝位置进行更新，得到一组新的鸟窝位置。

Step4计算更新后的鸟窝位置的适应度值，比较更新鸟窝的历史最佳位置。

Step5产生一个随机数r∈[0,1]与pa对比，保留被发现概率较小的鸟窝位置，同时随机改变被发现概率较大的鸟窝位置，得到一组新的鸟窝位置。

Step6判断算法是否满足结束条件，若满足，则输出结果，算法结束；否则，返回Step3。

3 布谷鸟搜索改进算法

3.1 种群初始化

在求解优化问题前无法预知全局最优解所在区域的情况下，初始种群个体必须充分代表解空间的个体，在有限数量内最大限度地表征所有个体的信息，这样才能使算法以较快的方式快速逼近最优解。

文献[9]认为，在基于种群迭代搜索的全局优化算法中，多样性较好的初始种群对寻找全局最优解很有帮助。然而，在CS算法中，通常在搜索空间中随机初始化种群，从而导致多样性较差。

混沌是一种非线性现象，具有随机性、遍历性等特点。本文利用混沌的遍历性产生初始群体。Tent混沌映射是一种能产生均匀序列且迭代速度快的混沌模型，其序列的迭代公式如下[10]：

其中，Xn∈[0,1]，n=1,2,…。

随机产生一个Q维的变量X=(x1, x2,…,xQ)，通过Zi=(xi-aj)/(bj-aj),i=1,2,…,Q 将变量X变换到混沌变量的取值区间[0,1]，然后根据式(3)进行M次迭代产生Zm(m=1,2,…,M)，将Z用式(4)将混沌序列还原到原优

i

i化变量取值区间，通过计算适应度值，从M个初始群体中选择适应度值较优的N个作为初始解。

其中，i=1,2,…,M ；j=1,2,…,Q；aj和bj分别为xij的取值范围。

3.2 惯性权重的引入

在基本CS算法中，布谷鸟寻窝的路径和位置是随机的，以父代位置信息为参考进行更新。为提高CS算法的性能，在布谷鸟寻窝的路径和位置更新公式中引入惯性权重：

惯性权重的引入，可使CS算法有扩展搜索空间的趋势，有能力搜索新的区域。一般来说，在全局优化算法中，总希望前期有较强的全局搜索能力，而在后期有较高的开发能力，以加快收敛速度。

实验结果表明，较大的惯性权重w有利于跳出局部最优，进行全局寻优；较小的w值有利于局部寻优，加速算法收敛。所以在迭代过程中，惯性权重w的值应随着迭代次数的增加而递减。本文采取一种惯性权重w线性递减策略：

其中，wmax和wmin分别是w的最大值和最小值；t和tmax分别为当前迭代次数和最大迭代次数。

3.3 动态随机局部搜索

文献[6]指出，CS算法具有较强的全局搜索能力，但局部搜索能力差，收敛速度慢。为了加快CS算法的收敛速度，增强其局部搜索能力，本文引入一种具有很强搜索能力的动态随机局部搜索技术，其具体步骤如下[11]：

Step1设定局部搜索代数E，搜索步长上限0α，对于每一个搜索步长αt的最大迭代次数为M，Xcurrent=Xbest，epoch = 0，k=0。

Step7如果m＜M，则转Step3；否则转Step8。

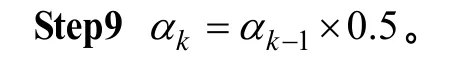
Step8k=k+1。 f(·)为计算适应值的函数。

3.4 改进CS算法

改进CS算法步骤如下：

Step1参数设置：最大迭代次数，种群规模N,α,Pa,E, M，惯性权重wmax,wmin。

Step2在搜索空间中利用混沌序列产生N个鸟窝的位置，令t=1。

Step3找出当前最优鸟窝位置和对应的最优适应度值。

Step4判断算法是否满足终止条件，若满足，则算法结束；否则，转Step5。

Step5按式(5)、式(6)和式(1)更新鸟窝的位置，得到新的鸟窝位置。

Step6随机产生一个均匀分布的数r∈[0,1]，如果r＞Pa，则随机改变发现概率较大的鸟窝位置，找出并保留最优鸟窝位置及对应值。

Step7利用算法对当前最优鸟窝位置进行局部寻优，令t=t+1，返回Step3。Step10如果epoch = E，则算法结束；否则返回Step2。epoch为局部搜索迭代计数器；Xbest为当前最优解；

4 数值实验

为评估本文提出的改进布谷鸟搜索(MCS)算法的性能，选取4个标准测试函数进行仿真实验，并与标准布谷鸟搜索(CS)算法进行比较，各测试函数的主要特征如表1所示。

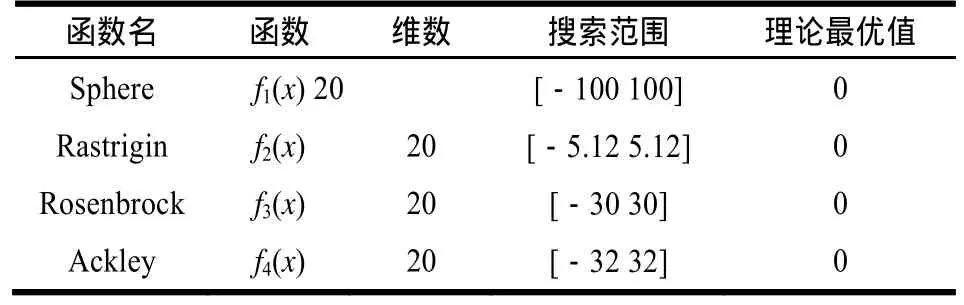
表1 4个标准测试函数

测试函数的数学表达式如下：

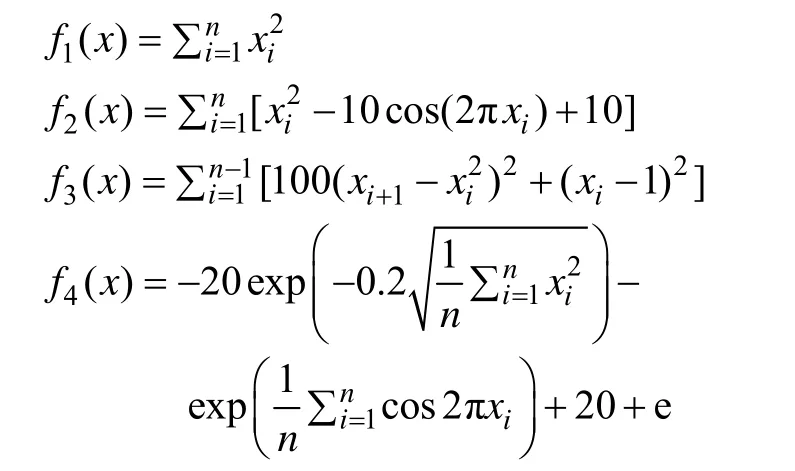
利用CS算法和MCS算法对上述4个标准测试函数进行实验。参数设置如下：在CS算法中，种群规模为25，α=1，Pa=0.25，最大迭代次数为1 000。在MCS算法中，种群规模为N=25，α=1，Pa=0.25，最大迭代次数为1 000，E=100，M=10，wmax=0.9，wmin=0.4。对每个测试函数，2种算法在上述参数设置下分别单独运行30次，记录最优值、平均值、最差值和标准差，比较结果如表2所示。

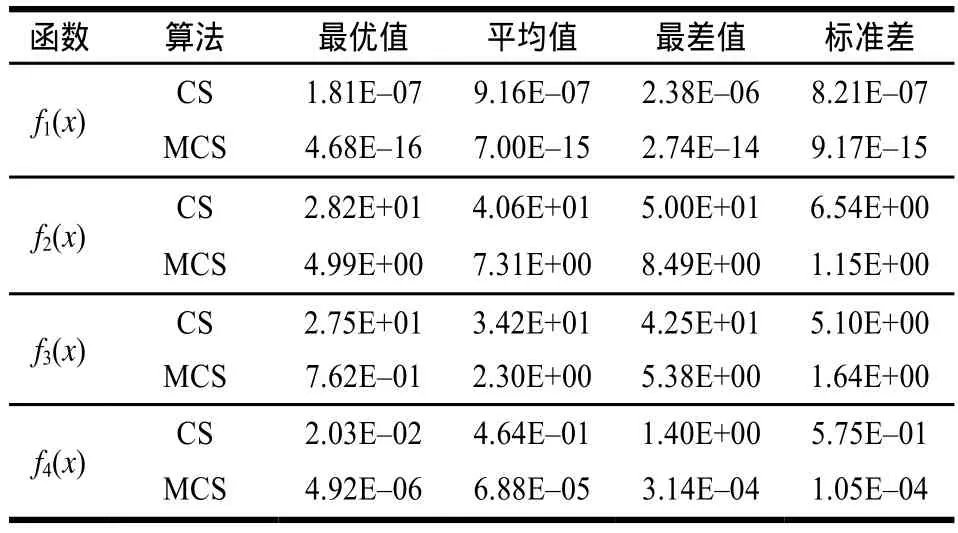
表2 CS算法和MCS算法的寻优结果比较

从表2可知，对于4个测试函数，MCS算法在30次实验中获得的最优值、平均值、最差值和标准差值均要优于CS算法，这充分说明无论是算法的收敛精度，还是算法的稳定性，MCS算法都比CS算法有了较大的提高。

图1～图4分别给出了CS算法和MCS算法对4个测试函数的收敛曲线，从图中可以看出，对于函数f1、f3和f4，MCS算法能很快收敛到最优解或接近最优解。

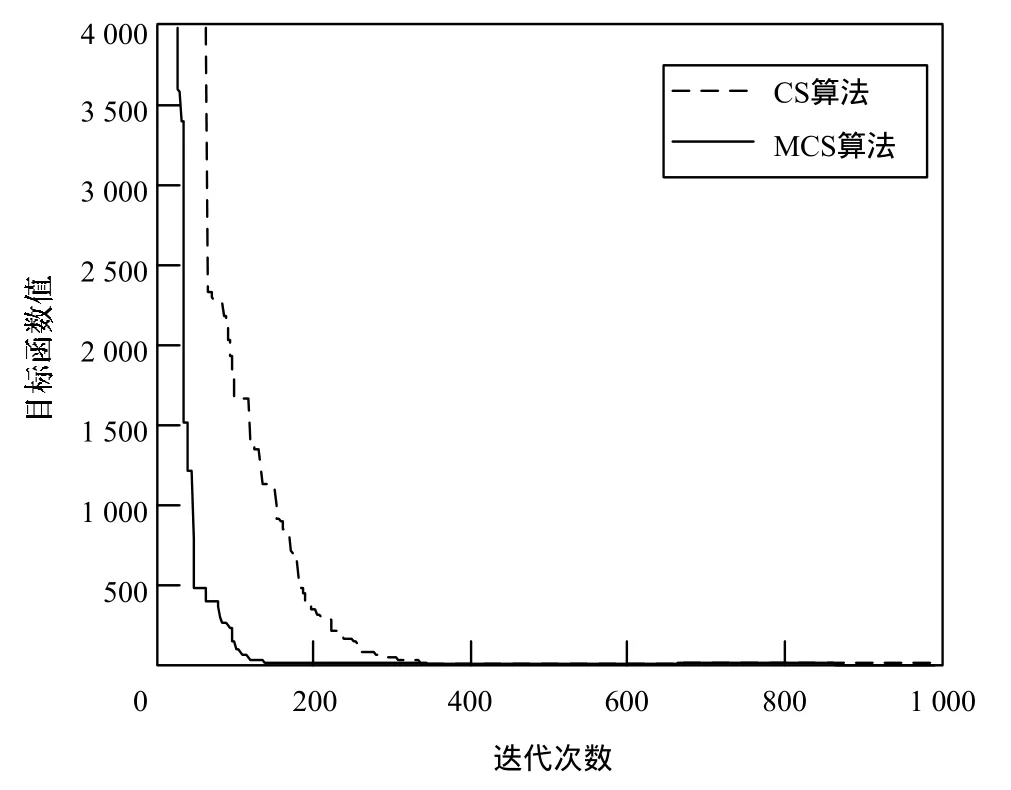
图1 f1函数的收敛性能比较

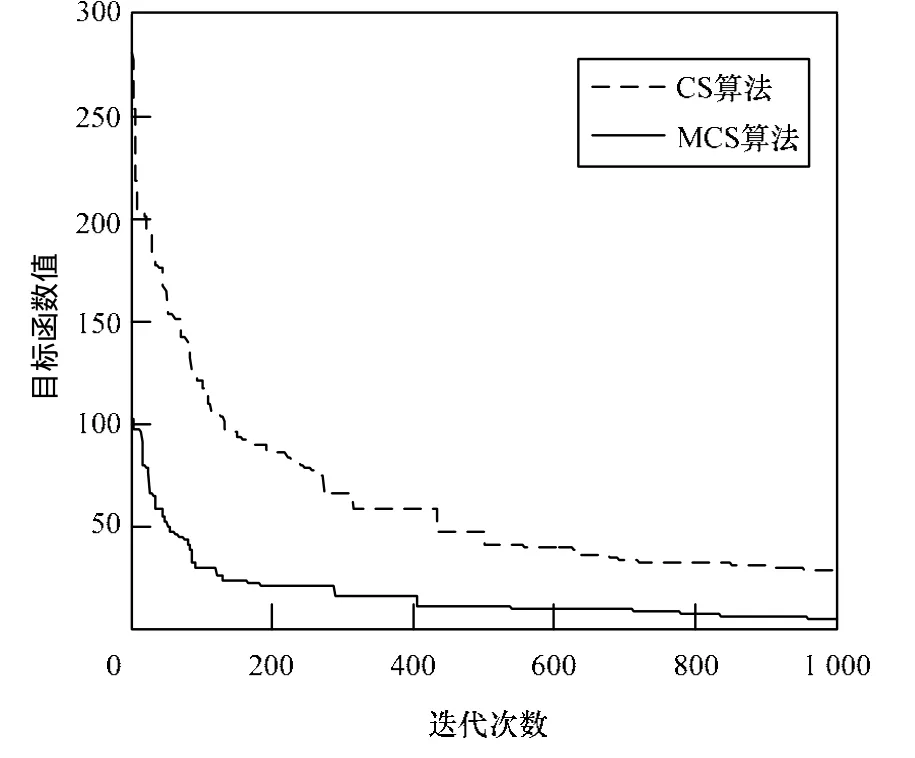
图2 f2函数的收敛性能比较

图3 f3函数的收敛性能比较

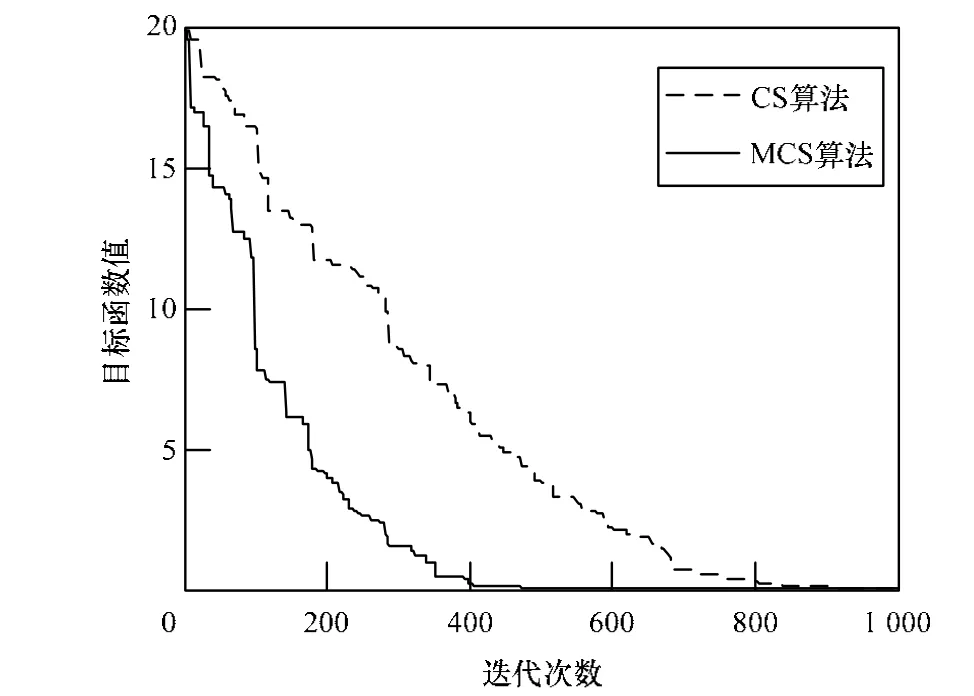
图4 f4函数的收敛性能比较

为了进一步说明MCS算法的有效性，将其与6种有代表性的智能优化算法的性能进行比较，它们分别是：遗传算法(Genetic Algorithm, GA)，进化策略(Evolution Strategy, ES)，粒子群优化(Particle Swarm Optimization, PSO)，蚁群优化(Ant Colony Optimization, ACO)，差分进化(Differential Evolution, DE)和生物地理优化(Biogeography-based Optimization, BBO)，6种算法的实验结果来源于文献[12]。表3给出了7种算法对测试函数f1～f4的寻优结果比较。

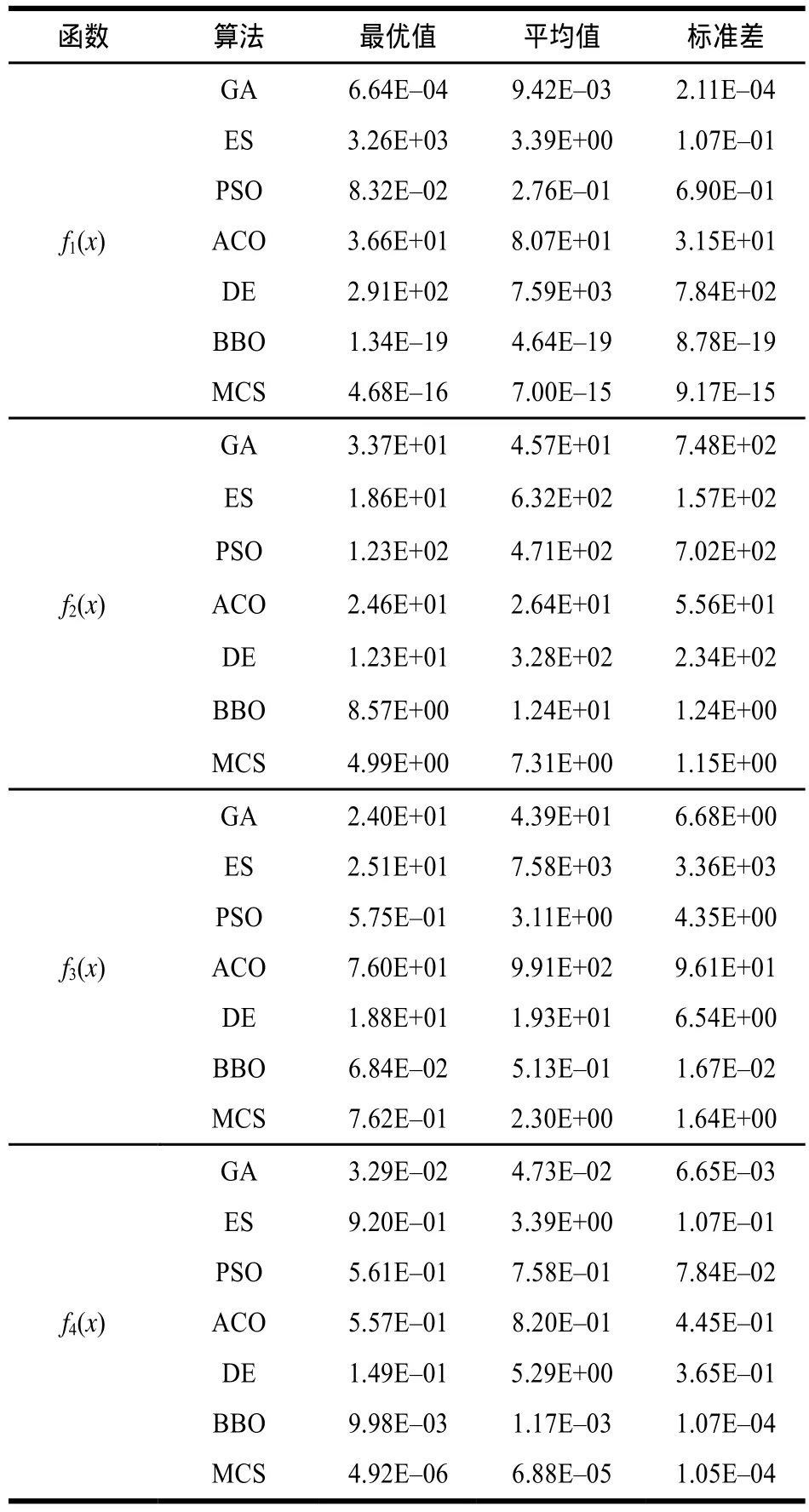
表3 MCS与其他6种算法的寻优结果比较

从表3可以看出，与GA、ES、PSO、ACO和DE算法相比，无论是获得最优解的精度，还是算法的稳定性，MCS算法在6个测试函数中得到的结果要优。与BBO算法相比，MCS算法在函数f2和f4上得到的结果要优，而在函数f1和f3上，BBO算法得到了较好的结果。从上述比较可知，MCS算法显示出较强的寻优性能。

5 结束语

针对布谷鸟搜索算法全局搜索能力强而局部搜索能力弱、易出现早熟收敛的缺点，本文提出一种有效的改进布谷鸟搜索算法。该算法利用混沌序列产生初始种群，为提高算法全局搜索能力奠定基础；引入惯性权重以平衡算法的勘探和开采能力；利用动态随机局部搜索技术进行局部搜索，以加快算法的收敛速度。针对4个标准测试函数的实验结果表明，该混合算法能有效地平衡其局部搜索和全局搜索性能。

[1] Yang Xinsh e, Deb S. Cucko o Search via L évy Flights[C]// Proc. of World Congress on Nature and Biologically Inspired Computing. [S. l.]: IEEE Press, 2009: 210-214.

[2] Gandomt A H, Y ang Xinsh e, Alavi A H. Cuckoo Search Algorithm: A M eta-heuristic A pproach to Solve Structural Optimization Problem[J]. Engineering with Computers, 2013, 29(1): 17-35.

[3] Y ang Xinshe, Deb S. Multi-obj ective Cuc koo Se arch fo r Design Optimization[J]. C omputers & O perations R esearch, 2013, 40(6): 1616-1624.

[4] B urnwal S, D eb S. Scheduling Optimizati on of Flexible Manu- facturing System Using Cuc koo S earch-based Approach[J]. International Journal of Advanced Manufacturing Technology, 2013, 64(5): 951-959.

[5] 柳新妮, 马 苗. 布谷鸟搜索算法在多阈值图像分割中的应用[J]. 计算机工程, 2013, 39(7): 274-278.

[6] 李向涛, 殷明浩. Parameter Estimation for Chaotic Systems Using the Cuckoo Search Algo rithm with an Orthogonal Learning Method[J]. 中国物理B: 英文版, 2012, 21(5).

[7] Zheng Hongqing, Zhou Yongquan. A Novel Cuckoo Search Optimization Algorithm Based on Gauss D istribution[J]. Journal of Computational Information Systems, 20 12, 8(10): 4193-4200.

[8] 杜利敏, 阮 奇, 冯登科. 基于共轭梯度的布谷鸟搜索算法[J]. 计算机与应用化学, 2013, 30(4): 406-410.

[9] Huapt R, Haupt S. Practical Genetic Algorithm[M]. [S. l.]: John Wiley & Sons, 2004.

[10] 刘悦婷. 基于混沌和动态变异的蛙跳算法[J]. 计算机应用与软件, 2012, 29(12): 137-140.

[11] Hamzacebi C. Improving Genetic Algorithms’ Performance by Local S earch f or Co ntinuous Function Optimization[J]. Applied Mathem atics and Compu tation, 2008, 1 96(1): 309-317.

[12] Ma Haiping. An Analysis of the Equilibrium of Migration Models for Biog eography-based Optimization[J]. Information Sciences, 2010, 180(18): 3444-3464.

编辑 顾逸斐

Modified Cuckoo Search Algorithm for Solving Unconstrained Optimization Problem

SU Fu-hua1a, LIU Yun-lian1b,2, WU Tie-bin1b

(1a. Department of Physics and Electronic Information; 1b. Department of Electrical and Mechanical Engineering, Hunan University of Humanities, Science and Technology, Loudi 417000, China; 2. College of Information and Electrical Engineering, Hunan University of Science and Technology, Xiangtan 411201, China)

Cuckoo Search(CS) algorithm is proposed as a population-based optimization algorithm and it is so far successfully applied in a variety of field s. A modified CS algorithm is proposed for solving unconstrained optimization problems. Chaos sequence and dynamic random local search technique are introduced to enhance the optimization ability and to improve the convergence speed of CS algorithm. Through testing the performance of the proposed algorithm on a set of 4 benchmark functions and comparing with other six algorithms, simulation result shows that the proposed algorithm has great ability of global search and better convergence rate.

Cuckoo Search(CS) algorithm; unconstrained optimization problem; chaotic; dynamic random local search; inertia weight; diversity

10.3969/j.issn.1000-3428.2014.05.046

国家自然科学基金资助项目(61174113)；湖南省教育厅基金资助一般项目(13C433)；湖南省科技厅基金资助项目(2014GK3 033, 2 013FJ6073)。

苏芙华(1976－)，女，讲师、硕士，主研方向：智能控制，安全监测；刘云连，助教；伍铁斌(通讯作者)，讲师、博士研究生。

2013-09-22

2013-11-13E-mail：wutiebin81@163.com

1000-3428(2014)05-0224-04

A

TP301.6