变速变桨距风力发电机组的智能控制

邓文斌 王维庆 吐松江·卡日 饶成诚 吴 寒 孟 威

(1.新疆大学电气工程学院，乌鲁木齐 830047；2.国网湖南省电力公司超高压管理局，长沙 410004；3.华润电力控股有限公司宜昌分公司，湖北 宜昌 443000)

目前，风力发电机组的控制技术已经由定桨距控制发展到变速变桨控制，其关键环节是控制策略和控制器的设计。为了提高电网的电能质量、降低风能转换系统所承受的载荷、最大限度地捕获风能并延长设备寿命[1,2]，笔者提出将机组输出功率的变化作为变桨距执行机构运行的判断标准。由于风力发电机组是非线性、强耦合的系统[3]，对于一个复杂多变量的不确定系统，采用模糊控制可以有效地满足其要求[4～6]，使其根据风速变化情况实现变速变桨运行。

1 变桨距控制理论①

风力发电机组主要由机械部分和电能转化部分组成。风轮是机械部分能量转换的关键部件，风以轴向风速流过风轮时捕获的功率为：

Pr=0.5πρCp(β,λ)R2ν3

(1)

式中Cp(β,λ)——风能利用系数；

Pr——风轮吸收的功率；

R——风轮半径；

ν——轴向风速，m/s；

ρ——空气密度。

风能利用系数Cp表示风能利用率，与叶尖速比λ和桨距角β成非线性函数关系：

(2)

根据式(2)可以获得风能利用系数的曲线，如图1所示。

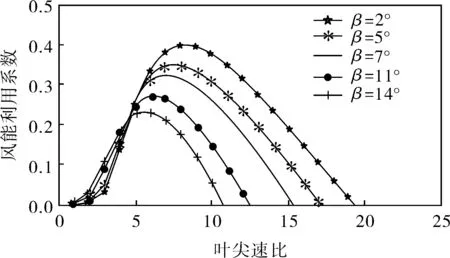
图1 风能利用系数曲线

从图1可知：

a. 对于某固定的桨距角β，存在唯一的最大风能利用系数Cpmax(β,λ)，且有最佳叶尖速比λopt；

b. 随着桨距角β的增大，风能利用系数Cp(β,λ)减小。

风力发电机组的参数值由风速、电机转速及发电机输出功率等因素实现独立控制，但由于风速的不确定性，一般通过电机的转速来反馈控制桨距角的变化[7]，从而实现变桨距控制。

2 传动系统模型

忽略传动链的内部动态过程，将其简化成单质量块。作用于单质量块传动链，对于非直驱式风力发电机组，其传动链运动方程为：

(3)

式中CT(β,λ)——风轮转矩系数；

Jr——风轮转动惯量；

Tm——齿轮箱转矩；

Tr——风轮转矩；

γ——齿轮箱的增速比；

ω——风轮转速。

当齿轮箱的转矩传递给发电机时，忽略发电机自身的系统阻力矩，其转动惯量为：

(4)

式中Jd——异步发电机转动惯量；

ωd——发电机转速，ωd=ωγ。

将式(3)、(4)结合，可得到风电机组传动系统方程：

(5)

3 控制系统设计

3.1 风电机组变速变桨控制策略

常规的风电机组变桨控制策略由风速大小而定。当风速低于额定风速时，风电机组可以视为定桨距运行；当风速高于额定风速时，此时实现变桨距运行以确保其安全稳定运行。

模糊控制属于智能控制，且具有数学模型不依赖于被控对象、鲁棒性好、抗干扰强及能克服非线性因素影响等优点，其可将专家的经验和知识表示成语言规则而实现控制，适用于难以建立精确数学模型的对象。根据功率的变化情况，通过模糊控制适时调整变桨距执行机构的变桨速度，实现其变速运行，与常规PI的变桨控制方法相比，变速变桨方案可以抑制超速、超载的出现，减轻变桨距执行机构的疲劳度，降低其故障发生率，延长使用寿命[8～10]。

假设风电机组额定功率为Ps，输出功率为P0，则功率误差为ΔP=P0-Ps，误差变化率为dΔP/dt。笔者研究瞬变风速在额定风速以上和额定风速以下的情况，风力机吸收的功率如图2所示。根据功率变化，再结合变速变桨风电机组的模糊控制策略，可推知：

a. 若ΔP<0，并且输出功率持续增大。当功率误差变化率增大时，变桨距执行机构减小桨距角，此过程减速变桨；当功率误差变化率保持不变时，变桨距执行机构减小桨距角，此过程保持当前变桨速度；当功率误差变化率减小时，变桨距执行机构减小桨距角，此过程加速变桨。

b. 若ΔP>0，并且输出功率持续增大。当功率误差变化率增大时，变桨距执行机构增大桨距角，此过程加速变桨；当功率误差变化率保持不变时，变桨距执行机构增大桨距角，此过程保持当前变桨速度；当功率误差变化率减小时，变桨距执行机构增大桨距角，此过程减速变桨。

c. 若在Ps处(即ΔP=0)变桨距执行机构不运行，保持当前桨距角不变。

d. 若ΔP>0，并且输出功率持续减小。当功率误差变化率增大时，变桨距执行机构增大桨距角，此过程加速变桨；当功率误差变化率保持不变时，变桨距执行机构增大桨距角，此过程保持当前变桨速度；当功率误差变化率减小时，变桨距执行机构增大桨距角，此过程减速变桨。

e. 若ΔP<0，并且输出功率持续减小。当功率误差变化率增大时，变桨距执行机构减小桨距角，此过程减速变桨；当功率误差变化率保持不变时，变桨距执行机构减小桨距角，此过程保持当前变桨速度；当功率误差变化率减小时，变桨距执行机构减小桨距角，此过程加速变桨。

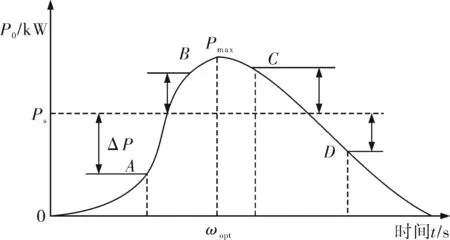
图2 风力机的吸收功率

由于传统的PI控制器属于反馈控制器，仅当偏差存在时，控制才起作用，并且在当时的风速下，整定好的PI参数合适，可能随着风速的变化其效果不一定理想。在此控制策略中，采用了模糊控制系统，无需根据实时测量的风速建立精确数学模型，只需通过功率变化情况、模糊控制器输出及时调整变桨速度，即可使风力发电机组稳定输出额定功率[11]。

3.2 模糊控制器的设计

模糊控制器非常适用于变速变桨风力发电机组这种非线性控制系统，因此笔者提出结合上述控制策略构建模糊控制器。系统控制结构如图3所示。

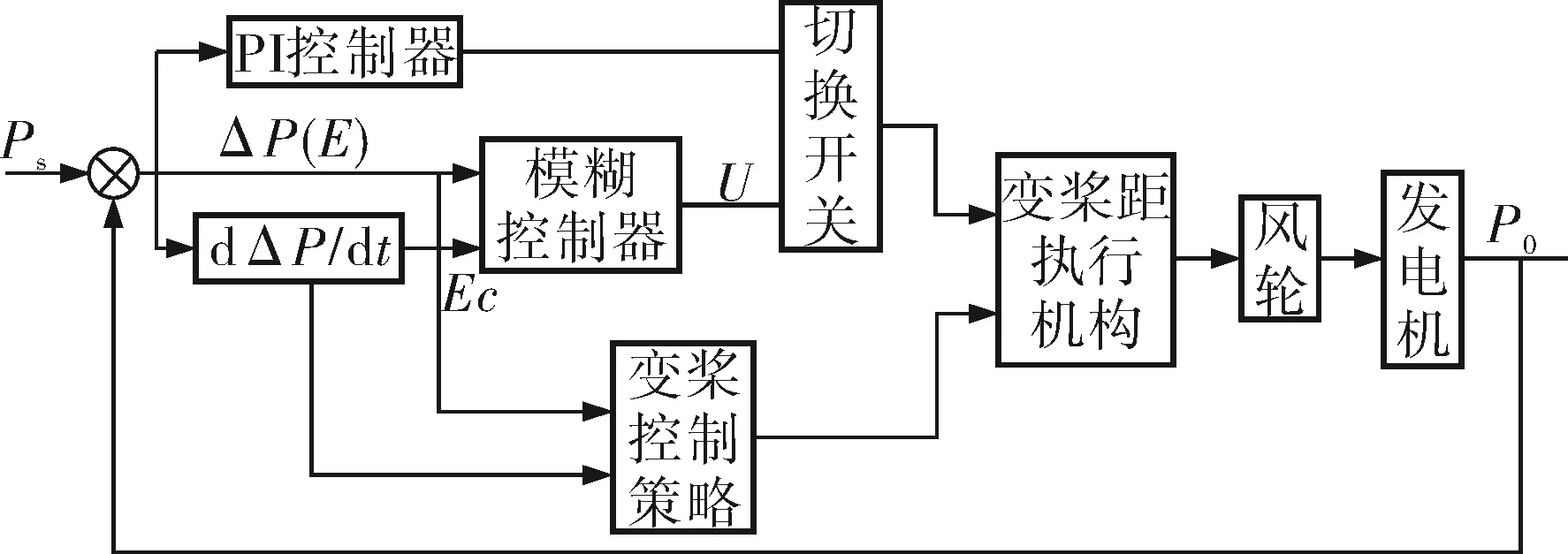
图3 系统控制结构框图

模糊控制的输入变量为功率误差E和误差变化率Ec，输出变量为变桨速度U。通过数据分析，结合专家经验，可得功率误差和误差变化率的基本论域为[-1×105W，1×105W]，取输出U的基本论域为[0°/s,5°/s]。输入变量和输出变量的量化因子与比例因子都是常数，合理地设计其值，使得控制器的输入、输出变量的基本论域分布在模糊论域[-6,6]，对应的模糊子集为{NB,NM,NS,ZO,PS,PM,PB}，分别用负大，负中，负小，零，正小，正中，正大表示。由此根据功率调节要求，结合经验可制定模糊控制规则(表1)。

4 仿真结果

在Matlab/Simulink仿真中，研究模拟的风力发电机组一般参数：空气密度ρ=1.25kg/m3，切入和切出风速分别为3m/s和25m/s，风轮和电机的转动惯量Jr=2.5×106kg·m2、Jd=52kg·m2，齿轮箱的传动比γ=79；额定功率为2MW，变桨距风力发电机组能够在风速不断变化中正常运行，发电机组模型如图4所示。

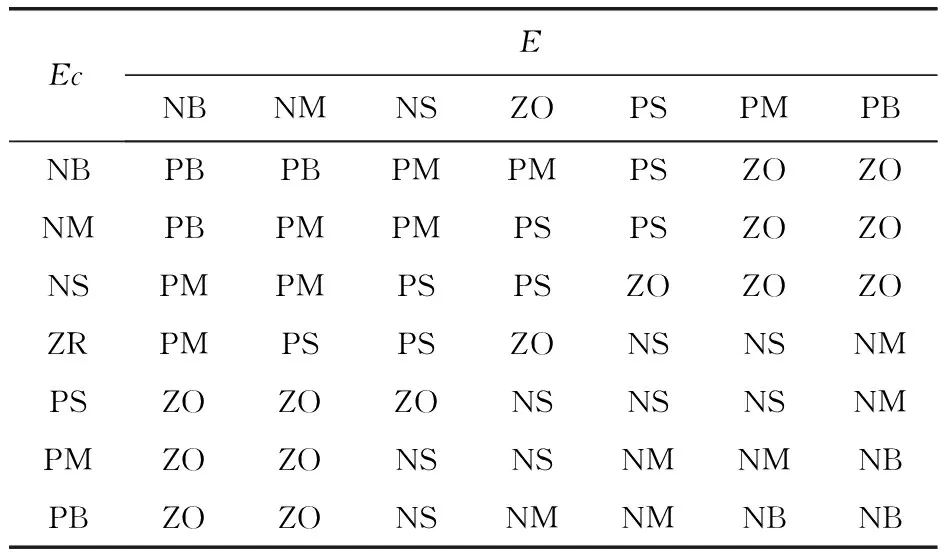
表1 模糊控制器规则

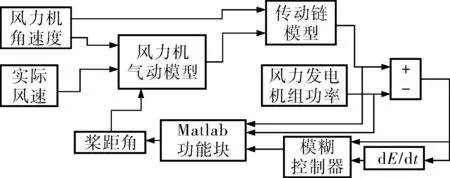
图4 变速变桨风力发电机组模型

当风速变化曲线如图5所示，仿真结果如图6所示，其中图6a为PI控制仿真结果,图6b为模糊控制仿真结果。

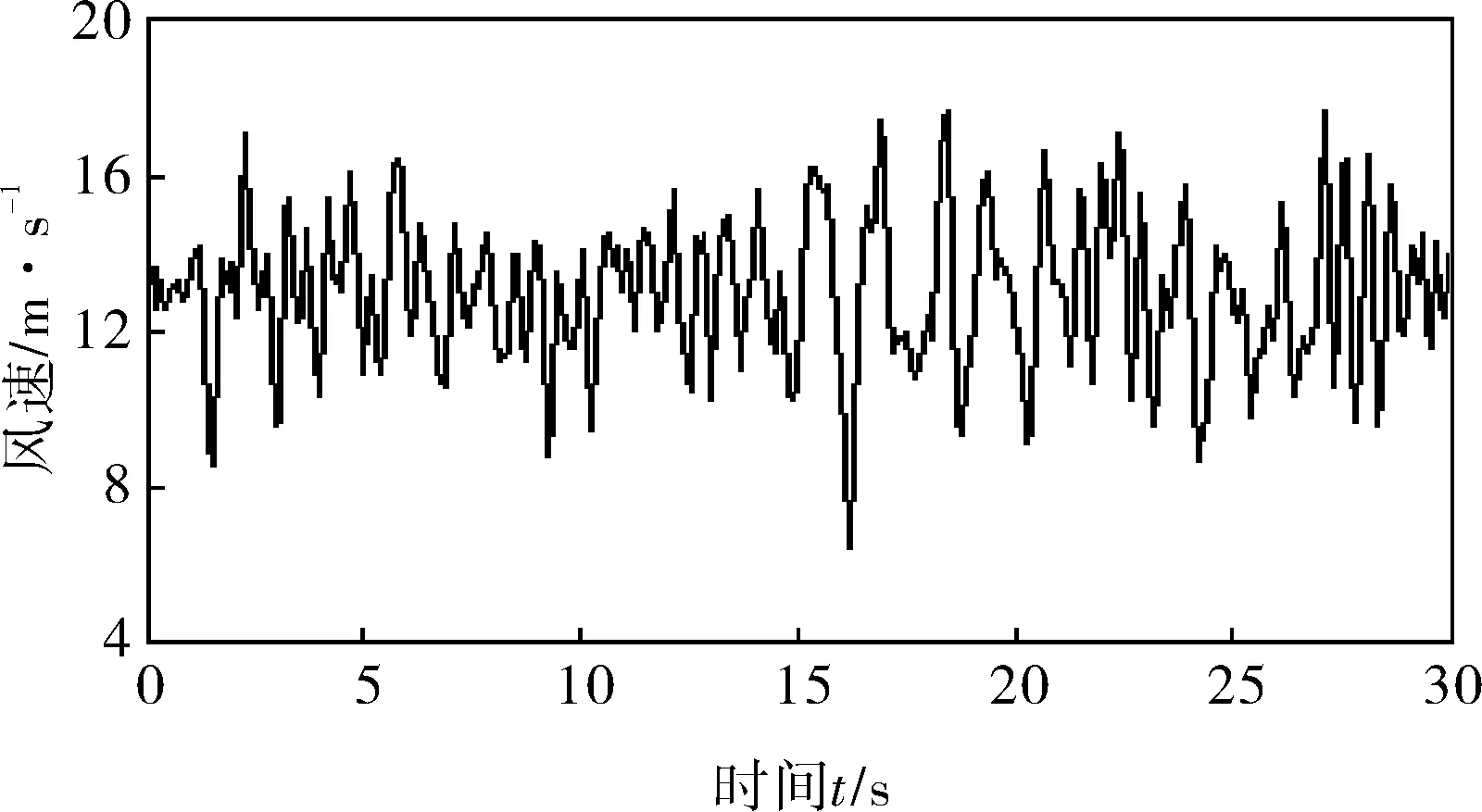
图5 风速变化曲线

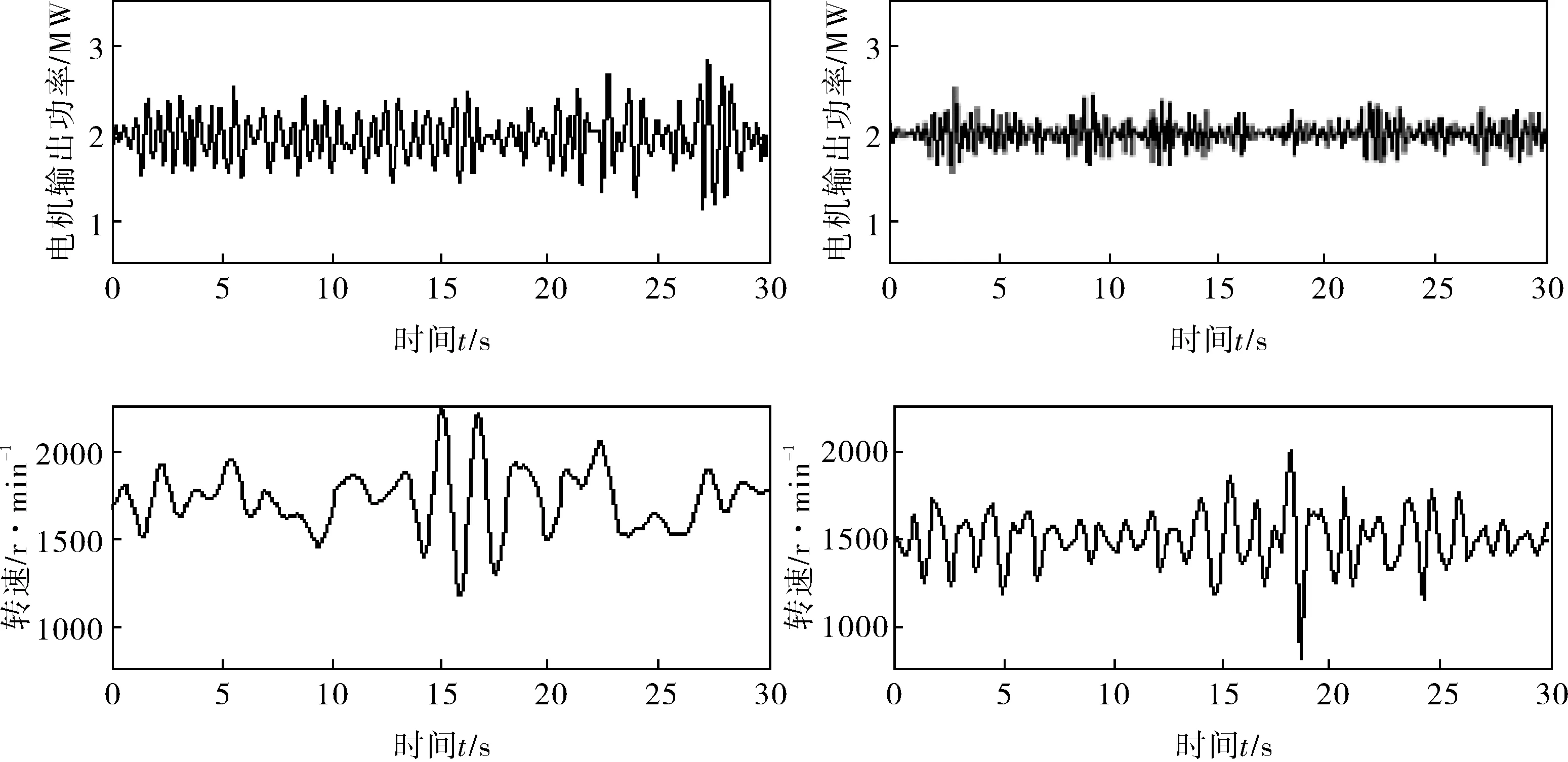
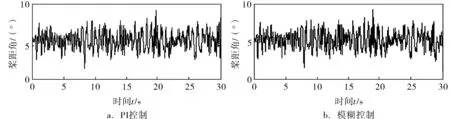
图6 仿真结果

可见，模糊控制时，随着风速不断的变化，模糊控制器可以快速实现小范围的桨距角调节，抑制系统功率输出的波动，从而降低电磁转矩的振动。但由于风力机惯性比较大，通过调节桨距角抑制功率波动需要一段响应时间。

通过仿真结果可得知，对比PI控制，笔者提出的基于功率变化作为变桨距控制策略的判断依据[12]，桨距角变化速度快，变桨幅值区间小。若瞬态风速高于额定风速时，电机输出功率幅值略高于额定功率，电机调节的转速小，从而达到安全稳定的输出功率。

5 结束语

笔者将模糊控制器引入变桨距控制系统中，结合一种基于功率变化判断的控制策略，实现风力发电机组在风速不断变化和瞬时变化的情况下迅速调节其输出功率的变速变桨控制方法。通过对比传统的PI控制器和模糊控制器的控制性能，可知所提模糊控制方法具有较强的鲁棒性，不要求精确的数学模型，可广泛应用于复杂的非线性系统。该模糊控制器弥补了传统PI控制器难以在电机高速运转和变桨距执行机构快速变桨的不足。